Statistiek voor Beginners | 5 Stappen & Voorbeelden
Statistiek heeft betrekking op het onderzoeken van trends, patronen en relaties met behulp van kwantitatieve data. Daarom is statistiek van groot belang als tool voor wetenschappers, studenten, de overheid, bedrijven en andere organisaties.
Het is belangrijk om vanaf het begin goed na te denken over je onderzoeksopzet en eventuele statistische analyses, zodat je valide conclusies kunt trekken. In je opzet specificeer je de hypothesen, en neem je beslissingen over je onderzoeksdesign, de steekproefgrootte en de steekproefmethode.
Na de dataverzameling kun je de data organiseren, structureren en samenvatten met behulp van beschrijvende statistiek (ook wel descriptieve statistiek genoemd). Vervolgens kun je inferentiële (toetsende of verklarende) statistiek gebruiken om hypothesen te toetsen en inschattingen te maken over de populatie. Ten slotte kun je de resultaten interpreteren en generaliseren.
Dit artikel vormt een introductie tot statistiek voor studenten en onderzoekers. We gebruiken twee voorbeelden om de vijf stappen toe te lichten. Het eerste voorbeeld gaat over een mogelijke causale relatie (oorzaak-gevolgrelatie) en het tweede voorbeeld over een potentiële correlatie tussen variabelen.
Inhoudsopgave
- Stap 1: Formuleer hypothesen en maak je onderzoeksdesign
- Stap 2: Verzamel data van een steekproef
- Stap 3: Vat je data samen met beschrijvende statistieken
- Stap 4: Toets je hypothesen of schat populatieparameters
- Stap 5: Interpreteer je resultaten
- Rapporteren van statistische resultaten
- Veelgestelde vragen
Stap 1: Formuleer hypothesen en maak je onderzoeksdesign
Om valide data te kunnen verzamelen voor je statistische analyses, is het van belang om eerst hypothesen op te stellen en je onderzoeksdesign uit te werken.
Statistische hypothesen formuleren
Het doel van onderzoek is vaak om een relatie tussen variabelen te onderzoeken voor een bepaalde populatie. Je begint met een voorspelling en je gebruikt statistiek om deze voorspelling te toetsen.
Een statistische hypothese is een formele voorspelling over de populatie. Iedere voorspelling wordt geformuleerd in twee delen: een nulhypothese (H0) en een alternatieve hypothese (H1). Deze kunnen worden getoetst met behulp van steekproefdata.
De nulhypothese voorspelt altijd dat er geen sprake is van een effect of relatie, terwijl de alternatieve hypothese een voorspelling van een effect of relatie weergeeft.
- Nulhypothese: Een meditatie-oefening van 5 minuten heeft geen effect op de toetsscores van universitaire studenten.
- Alternatieve hypothese: Een meditatie-oefening van 5 minuten verhoogt de toetsscores van universitaire studenten.
- Nulhypothese: Er bestaat geen verband tussen het ouderlijk inkomen en de taalscore op de eindtoets van middelbare scholieren.
- Alternatieve hypothese: Er bestaat een positieve correlatie tussen het ouderlijk inkomen en de taalscore op de eindtoets van middelbare scholieren.
Je onderzoeksdesign uitwerken
Een onderzoeksdesign bevat je strategie voor de dataverzameling en data-analyse. Dit design bepaalt welke statistische toetsen je in een later stadium kunt gebruiken om je hypothese te toetsen.
Bepaal eerst of je voor een beschrijvend (descriptief) onderzoek, correlationeel onderzoek of experimenteel design gaat. Bij experimenten manipuleer je variabelen, terwijl je bij beschrijvende en correlationele onderzoeken alleen variabelen meet.
- In een experimenteel design kun je een verwachte causale relatie onderzoeken (zoals het effect van meditatie op toetsscores) door vergelijkende analyses of regressieanalyses te gebruiken.
- In een correlationeel design kun je de relaties tussen variabelen onderzoeken (zoals de relatie tussen het ouderlijk inkomen en de taalscore), zonder dat hierbij sprake hoeft te zijn van causaliteit. Dit doe je met behulp van correlatiecoëfficiënten en significantietoetsen.
- In een beschrijvend design kun je de eigenschappen van een populatie of fenomeen onderzoeken (zoals de prevalentie van angststoornissen bij Nederlandse studenten). Je gebruikt statistische analyses om eigenschappen af te leiden uit steekproefdata.
In je onderzoeksdesign geef je ook aan of je participanten vergelijkt op groepsniveau, individueel niveau of beide.
- In een between-subjects design vergelijk je de groepsgemiddelden van participanten die zijn blootgesteld aan verschillende condities (bijvoorbeeld de groep die wel een meditatie-oefening heeft gedaan en de groep die dat niet heeft gedaan).
- In een within-subjects design vergelijk je de uitkomsten van participanten die zijn blootgesteld aan alle condities (bijvoorbeeld scores van voor en na de meditatie-oefening).
- In een mixed design vergelijk je uitkomsten zowel op groepsniveau als individueel niveau. Dit komt bijvoorbeeld voor als je de groep die wel een meditatie-oefening heeft gedaan vergelijkt met de groep die dat niet heeft gedaan, terwijl je ook kijkt naar de scores van individuen op verschillende meetmomenten (herhaaldelijke metingen van bijvoorbeeld een pretest, posttest en follow-uptest).
Allereerst zorg je voor een nulmeting (voorafgaand aan de meditatie). Vervolgens nemen je participanten deel aan een meditatie-oefening van 5 minuten. Ten slotte verzamel je nog een keer toetsscores bij een tweede toets die na de oefening plaatsvindt.
In dit experiment is de meditatie-oefening van 5 minuten de onafhankelijke variabele, en de afhankelijke variabele is de toetsscore.
Er zijn geen afhankelijke of onafhankelijke variabelen in dit onderzoek, omdat je alleen variabelen wilt meten zonder ze te beïnvloeden.
Variabelen meten
Als je een onderzoeksdesign maakt, moet je je variabelen operationaliseren en beslissen hoe je ze precies gaat meten.
In het geval van een statistische data-analyse is het belangrijk om rekening te houden met het meetniveau van je variabelen, omdat dit niveau iets zegt over de aard van de data:
- Categorische data laten groepen zien. Deze data kunnen nominaal zijn (zoals geloofsovertuiging), maar ook ordinaal (zoals taalniveau).
- Kwantitatieve data representeren hoeveelheden. Deze data kunnen van intervalniveau (zoals IQ-scores) of rationiveau (zoals leeftijden) zijn.
Veel variabelen kunnen op verschillende niveaus worden gemeten. Leeftijden kunnen bijvoorbeeld kwantitatief (8, 9, 10 jaar oud) of categorisch (kind, jongere, volwassene, oudere) zijn. Als een variabele numeriek is gecodeerd (bijvoorbeeld “mate van overeenstemming” op een schaal van 1 tot 5), betekent dit niet automatisch dat deze kwantitatief is in plaats van categorisch.
Het is essentieel om het meetniveau van tevoren te bepalen, omdat je keuze ook direct bepaalt welke statistieken en toetsen je kunt gebruiken. Je kunt bijvoorbeeld wel een gemiddelde berekenen voor kwantitatieve data, maar niet voor categorische.
Bij een onderzoek verzamel je meestal niet alleen gegevens over de variabelen waarin je geïnteresseerd bent, maar kijk je ook naar relevante participantkenmerken (en/of controlevariabelen).
| Variabele | Type data |
|---|---|
| Leeftijd | Kwantitatief (ratio) |
| Gender | Categorisch (nominaal) |
| Etniciteit | Categorisch (nominaal) |
| Nulmeting toetsscores | Kwantitatief (interval) |
| Laatste meting toetsscores | Kwantitatief (interval) |
| Variabele | Type data |
|---|---|
| Ouderlijk inkomen | Kwantitatief (ratio) |
| Taalscore op eindtoets | Kwantitatief (interval) |
Lees waarom zo veel studenten Scribbr inschakelen
Stap 2: Verzamel data van een steekproef
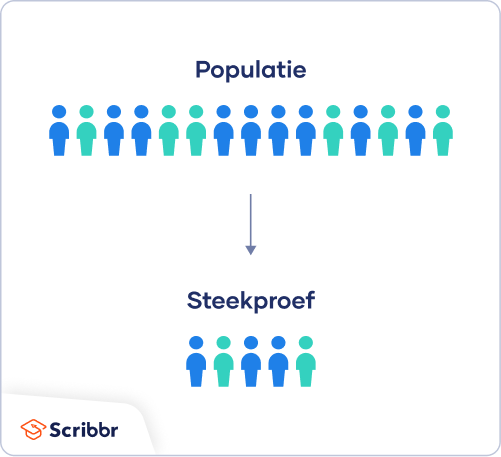
In de meeste gevallen is het te moeilijk of te duur om gegevens te verzamelen van elk lid van de populatie waarin je geïnteresseerd bent. In plaats daarvan verzamel je gegevens voor een subset van de populatie. Dit is je steekproef.
Met statistische analyses kun je je bevindingen generaliseren naar de populatie, mits je de juiste steekproefmethode hebt gebruikt. Het is belangrijk om te streven naar een representatieve steekproef, zodat de populatie goed wordt weerspiegeld.
Steekproeven voor statistische analyses
Er zijn twee methoden om een steekproef te trekken:
- Aselecte steekproef (probability sampling): ieder lid van de populatie heeft een even grote kans om te worden geselecteerd voor deelname aan het onderzoek.
- Selecte steekproef (non-probability sampling): sommige leden van de populatie hebben een grotere kans dan andere leden om te worden geselecteerd voor het onderzoek.
In theorie moet je een aselecte steekproef trekken om je bevindingen te kunnen generaliseren. Willekeurige selectie vermindert het risico op een steekproefbias (sampling bias) en zorgt ervoor dat de data daadwerkelijk representatief zijn voor de populatie. Je kunt parametrische toetsen gebruiken om sterke statistische conclusies te trekken, mits je de data verzamelt met een aselecte steekproef.
In de praktijk is het bijna nooit mogelijk om de ideale steekproef te verzamelen. Selecte steekproeven zorgen eerder voor vertekende data dan aselecte steekproeven, maar het is wel veel makkelijker om voldoende participanten te werven en data te verzamelen. Niet-parametrische toetsen zijn geschikter voor selecte steekproeven, maar ze resulteren wel in zwakkere conclusies over de populatie.
Als je parametrische toetsen wilt gebruiken voor selecte steekproeven, moet je beargumenteren dat:
- je steekproef representatief is voor de populatie waar je de resultaten naar wilt generaliseren.
- er geen sprake is van een systematische onderzoeksbias in je steekproef.
Houd er rekening mee dat je je conclusies alleen kunt generaliseren naar populaties die kenmerken delen met de steekproef. Zo is het niet altijd mogelijk om resultaten van westerse, opgeleide, geïndustrialiseerde, rijke en democratische steekproeven te generaliseren naar populaties die deze eigenschappen niet delen.
Als je parametrische toetsen gebruikt voor selecte steekproeven, is het van belang om in je discussiesectie uitgebreid in te gaan op de beperkingen van de externe validiteit (en dus de generaliseerbaarheid).
Kies een geschikte steekproefmethode
Je bepaalt de manier waarop je participanten verzamelt op basis van de beschikbare middelen voor je onderzoek.
- Heb je de middelen om je onderzoek overal te promoten, ook buiten de setting van je eigen onderwijsinstelling?
- Ben je in staat om een diverse steekproef te trekken, die representatief is voor een brede populatie?
- Heb je tijd om leden van moeilijk te bereiken groepen (meerdere keren) te contacteren?
De studiecoördinatoren selecteren zelf participanten. Hoewel je een selecte steekproef gebruikt, streef je naar een diverse en representatieve steekproef.
Je participanten melden zichzelf vrijwillig aan voor je onderzoek, waardoor sprake is van een selecte steekproef.
Bereken de vereiste steekproefgrootte
Bepaal voorafgaand aan het werven van participanten hoe groot de steekproef moet zijn. Je kunt hiervoor naar andere onderzoeken uit je vakgebied kijken, maar het is beter om berekeningen te gebruiken. Een te kleine steekproef kan ertoe leiden dat je data niet representatief zijn voor de populatie, en een te grote steekproef kan je onderzoek onnodig duur maken.
Er zijn veel online rekenmachines om de vereiste steekproefomvang te berekenen. De tools gebruiken verschillende formules, afhankelijk van de aanwezigheid van subgroepen en eventuele striktheidseisen (bijvoorbeeld bij klinisch onderzoek). Als vuistregel kun je onthouden dat je minimaal 30 participanten per subgroep nodig hebt.
Om de online calculator te gebruiken, moet je vaak enkele gegevens aanleveren:
- Het significantieniveau (alfa): het risico dat je een juiste nulhypothese verwerpt. Je kiest dit percentage zelf, maar alfa is meestal gelijk aan 5%.
- Statistische power: de kans dat je met je onderzoek een effect vindt dat daadwerkelijk bestaat. Hiervoor kies je meestal 80% of hoger.
- Verwachte effectgrootte: een gestandaardiseerde indicatie van de grootte van het verwachte effect van je onderzoek. Deze waarde baseer je vaak op andere onderzoeken.
- Standaarddeviatie van de populatie: een schatting van de populatieparameter. Deze waarde baseer je op een vergelijkbaar onderzoek of je eigen pilotonderzoek.
Stap 3: Vat je data samen met beschrijvende statistieken
Zodra je alle data hebt verzameld, kun je de gegevens inspecteren en ze met behulp van beschrijvende statistieken samenvatten.
Inspecteer de data
Je kunt je data op verschillende manieren inspecteren, bijvoorbeeld op de volgende manieren:
- Organiseer de data voor iedere variabele in frequentietabellen (frequency distribution tables).
- Geef de data voor een belangrijke variabele weer in een staafdiagram (bar chart) om verdeling te zien.
- Visualiseer de relatie tussen twee variabelen met behulp van een scatterplot.
Door de gegevens te visualiseren met behulp van tabellen en grafieken, kun je beoordelen of je data normaal verdeeld zijn. Bovendien kun je vaststellen of er missende gegevens of uitbijters (ook uitschieters of outliers genoemd) zijn.
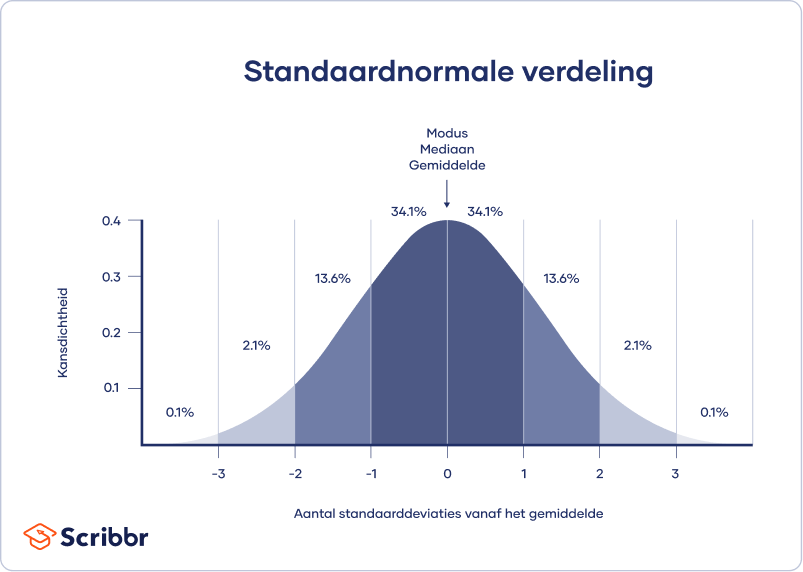
Een normale verdeling betekent dat de gegevens symmetrisch zijn verdeeld rond een centrum waar de meeste waarden liggen, waarbij de waarden aan de uiteinden taps toelopen. Hierdoor ontstaat een klokvorm.
Een scheve verdeling (skewed distribution) is juist asymmetrisch en heeft aan de ene kant meer waarden dan aan de andere kant. Het is belangrijk om te bepalen of je te maken hebt met normaal verdeelde data, omdat je bij een scheve verdeling maar enkele beschrijvende statistieken mag gebruiken.
Extreme uitbijters kunnen ook misleidende statistieken opleveren, dus het kan zijn dat je deze eerst systematisch moet verwijderen voordat je statistieken kunt berekenen.
Bereken centrummaten
Centrummaten (measures of central tendency) beschrijven waar de meeste waarden in een dataset zich bevinden. Je rapporteert vaak (een van) de volgende drie centrummaten:
- Modus (mode): de waarde die het vaakst voorkomt in de dataset.
- Mediaan (median): de middelste waarde als je alle waarden van klein naar groot zet.
- Gemiddelde (mean): de som van alle waarden, gedeeld door het aantal waarden.
Afhankelijk van de vorm van de verdeling en het meetniveau kun je vaak maar één of twee van deze maten gebruiken. Veel demografische kenmerken kunnen bijvoorbeeld alleen worden beschreven met behulp van de modus of verhoudingen, terwijl een variabele zoals reactietijd soms helemaal geen modus kan hebben (omdat iedereen een andere tijd heeft).
Bereken spreidingsmaten
Spreidingsmaten (measures of variability) vertellen je iets over hoe verspreid de waarden in een dataset zijn. Je rapporteert vaak (een van) de volgende vier maten:
- Bereik (range): het verschil tussen de hoogste en laagste waarde uit de dataset.
- Interkwartielafstand (interquartile range): het bereik van het middelste deel van de dataset.
- Standaarddeviatie (standard deviation): de gemiddelde afstand tussen iedere waarde in de dataset en het gemiddelde.
- Variantie (variance): de standaarddeviatie in het kwadraat.
Ook in het geval van spreidingsmaten bepalen de vorm van de verdeling en het meetniveau deels je keuze voor de juiste maten. De interkwartielafstand is de beste maat voor scheve verdelingen, terwijl de standaarddeviatie en variantie de beste informatie geven voor normale verdelingen.
Controleer aan de hand van je tabel of de beschrijvende statistieken vergelijkbaar zijn voor pretest- en posttestscores. Zijn de variantieniveaus van beide groepen bijvoorbeeld vergelijkbaar? Zijn er extreme waarden? Als dat het geval is, kan het voorkomen dat je de extreme uitbijters in je dataset moet identificeren en verwijderen of dat je je gegevens transformeren voordat je een statistische analyse kunt uitvoeren.
| Pretest-scores | Posttest-scores | |
|---|---|---|
| Gemiddelde | 68,44 | 75,25 |
| Standaarddeviatie | 9,43 | 9,88 |
| Variantie | 88,96 | 97,96 |
| Bereik | 36,25 | 45,12 |
| N | 30 | |
Uit deze tabel kunnen we opmaken dat de gemiddelde toetsscore toenam na de meditatie-oefening, en dat de varianties vergelijkbaar zijn. Daarom kunnen we een statistische analyse uitvoeren om te bepalen of deze verbetering in toetsscores statistisch significant is in de populatie.
Het is belangrijk om te controleren of je een breed scala aan datapunten hebt. Als je dat niet doet, kan het voorkomen dat je data meer gericht zijn op bepaalde groepen dan op andere (bijvoorbeeld veel theoretisch opgeleide deelnemers en bijna geen praktisch opgeleide participanten). In dat geval kun je geen sterke conclusies trekken over een relatie en zijn de resultaten moeilijk te generaliseren.
| Bruto ouderlijk inkomen (€) | Taalscore (1-5) | |
|---|---|---|
| Gemiddelde | 62.100 | 3,12 |
| Standaarddeviatie | 15.000 | 0,45 |
| Variantie | 225.000.000 | 0,16 |
| Bereik | 8.000–378.000 | 2,64–4,00 |
| N | 653 | |
Vervolgens kun je een correlatiecoëfficiënt berekenen en een statistische analyse uitvoeren om te bepalen of de eventuele relatie tussen variabelen in de populatie significant blijkt te zijn.
Stap 4: Toets je hypothesen of schat populatieparameters
Een getal dat een steekproef beschrijft, wordt een statistiek genoemd, terwijl een getal dat de populatie beschrijft een parameter wordt genoemd. Met behulp van toetsende statistiek (ook wel verklarende of inferentiële statistiek genoemd) kun je conclusies trekken over de populatie-parameters op basis van de steekproefstatistieken.
Onderzoekers gebruiken vaak twee methoden (op hetzelfde moment) om statistische conclusies te kunnen trekken:
- Schatting (estimation): populatieparameters berekenen op basis van steekproefstatistieken.
- Hypothesen toetsen: een proces waarbij je verwachtingen over de populatie toetst op basis van steekproeven.
Schatting
Je kunt populatieparameters op twee manieren schatten met behulp van steekproefstatistieken:
- Een puntschatting (point estimate): een waarde die de beste schatting van de exacte parameter representeert.
- Een intervalschatting (interval estimate): een interval dat de beste schatting geeft van het bereik waarbinnen de parameter ligt.
Als het je doel is om populatiekenmerken af te leiden uit steekproefdata, kun je het beste zowel punt- als intervalschattingen gebruiken.
Je kunt een steekproefstatistiek zien als een puntschatting voor de populatieparameter als er sprake is van een representatieve steekproef. Bij een publieke opiniepeiling wordt bijvoorbeeld geschat hoeveel mensen op een bepaalde partij stemmen op basis van een hele brede steekproef.
Schattingen bevatten altijd fouten, dus je geeft ook een betrouwbaarheidsinterval om de spreiding rond een puntschatting te laten zien.
Een betrouwbaarheidsinterval is gebaseerd op de standaardfout (standard error) en de z-score van de standaard normaalverdeling, en geeft aan binnen welk interval je de populatieparameter verwacht te vinden.
Hypothese toetsen
Met behulp van steekproefdata kun je hypothesen toetsen over relaties tussen variabelen in de populatie. Het toetsen van hypothesen begint met de aanname dat de nulhypothese waar is. Vervolgens gebruik je statistische toetsen om te bepalen of de nulhypothese kan worden verworpen of niet.
Statistische toetsen bepalen waar de steekproefdata zich zouden bevinden op een verwachte verdeling van de steekproefdata als de nulhypothese waar zou zijn. Deze toetsen geven twee belangrijke resultaten:
- Een toetsstatistiek (test statistic) vertelt je in welke mate je data verschillen van de nulhypothese van de toets.
- Een p-waarde toont je de kans dat je deze resultaten zou vinden als de nulhypothese waar zou zijn voor de populatie. Deze waarde laat dus zien hoe groot de kans is dat je dit resultaat hebt gevonden door toeval en niet door de oorzaak die je onderzoekt.
Over het algemeen genomen wordt een onderscheid gemaakt tussen drie soorten statistische toetsen:
- Met vergelijkingstoetsen (comparison tests) onderzoek je groepsverschillen in je resultaten.
- Met regressietesten onderzoek je oorzaak-gevolgrelaties tussen variabelen.
- Met correlatietoetsen onderzoek je relaties tussen variabelen zonder causaliteit te veronderstellen.
Je keuze voor een statistische toets is afhankelijk van je onderzoeksvragen, onderzoeksdesign, steekproefmethode, en de eigenschappen van je data.
Parametrische toetsen
Met parametrische toetsen kun je sterke conclusies trekken over de populatie op basis van steekproefdata. Je data moeten wel aan enkele assumpties of aannames voldoen om deze toetsen te kunnen gebruiken. Als je gegevens de aannames schenden, kun je datatransformaties uitvoeren of niet-parametrische toetsen gebruiken.
Een regressie modelleert de mate waarin veranderingen in een voorspellende variabele resulteren in veranderingen in uitkomstvariabele(n).
- Een enkelvoudige lineaire regressie (simple linear regression) heeft betrekking op één voorspellende variabele en één uitkomstvariabele.
- Een meervoudige lineaire regressie (multiple linear regression) heeft betrekking op twee of meer voorspellende variabelen en één uitkomstvariabele.
Met vergelijkingstoetsen vergelijk je meestal groepsgemiddelden. Dit kunnen de gemiddelden van verschillende groepen binnen één steekproef zijn (bijvoorbeeld een experimentele en controlegroep), maar ook de gemiddelden van één steekproefgroep op verschillende momenten (bijvoorbeeld pretest- en posttest-scores), of een vergelijking van een steekproefgemiddelde en een populatiegemiddelde.
- Een t-toets (ook wel t-test genoemd) is geschikt voor de vergelijking van 1 of 2 groepen in het geval van een kleine steekproef (30 of minder).
- Een z-toets (ook wel z-test genoemd) is geschikt voor de vergelijking van 1 of 2 groepen in het geval van een grote steekproef.
- Een ANOVA is geschikt voor de vergelijking van drie of meer groepen.
De z-toets en t-toets kunnen nog verder worden opgedeeld in subtypes, gebaseerd op het aantal steekproeven, de aard van de steekproeven, en de hypothesen:
- Als je één steekproef wilt vergelijken met een populatiegemiddelde, gebruik je een one-sample test.
- Als je gepaarde metingen hebt vanwege een within-subjects design, gebruik je een afhankelijke (gepaarde) t-toets (dependent/paired samples test).
- Als je onafhankelijke metingen hebt van twee ongepaarde groepen vanwege een between-subjects design, gebruik je een onafhankelijke (ongepaarde) t-toets (independent/unpaired samples test).
- Als je een verschil tussen groepen verwacht in een bepaalde richting, gebruik je een eenzijdige toets (one-tailed test).
- Als je geen verwachtingen hebt voor de richting van een verschil tussen groepen, gebruik je een tweezijdige toets (two-tailed test).
De enige parametrische correlatietoets, is Pearson’s r. De correlatiecoëfficiënt (r) laat zien hoe sterk de lineaire relatie tussen twee kwantitatieve variabelen is.
Om te toetsen of de correlatie in de steekproef sterk genoeg is om van belang te zijn in de populatie, moet je ook een significantietoets uitvoeren op de correlatiecoëfficiënt om een p-waarde te verkrijgen. Deze toets maakt gebruik van de steekproefomvang om te berekenen hoeveel de correlatiecoëfficiënt van nul verschilt in de populatie.
Je gebruikt een eenzijdige afhankelijke t-toets om te beoordelen of de meditatie-oefening de toetsscores significant verbeterde. De toets geeft je:
- een t-waarde (toetsstatistiek) van 3.00
- een p-waarde van 0.0028
Hoewel Pearson’s r een toetsstatistiek is, zegt de waarde niets over de significantie van de correlatie in de populatie. Je moet dus nog toetsen of de correlatiecoëfficiënt groot genoeg is om een correlatie in de populatie aan te tonen.
Een t-toets kan op basis van de steekproefomvang bepalen hoe significant een correlatiecoëfficiënt verschilt van nul. Aangezien je een positieve correlatie verwacht tussen het ouderlijk inkomen en de taalscore, gebruik je een eenzijdige one-sample t-toets.
De t-toets geeft je:
- een t-waarde van 3.08
- een p-waarde van 0.001
Stap 5: Interpreteer je resultaten
De laatste stap van een statistische analyse is het interpreteren van je resultaten.
Statistische significantie
Bij het toetsen van hypotheses, baseer je je conclusie voornamelijk op de statistische significantie. Je vergelijkt je p-waarde met een vooraf vastgesteld significantieniveau (meestal 0.05) om te bepalen of je resultaten statistisch significant zijn (of juist niet).
Als een resultaat statistisch significant is, is de kans bijzonder klein dat je dit resultaat gevonden hebt op basis van toeval. Er is daardoor ook maar een hele kleine kans dat je dat resultaat nog een keer vindt als de nulhypothese waar is voor populatie.
Dit betekent dat je gelooft dat de meditatie-interventie de toegenomen toetsscores heeft veroorzaakt en dat willekeurige factoren geen rol hebben gespeeld.
Correlatie betekent niet altijd dat er ook sprake is van causaliteit. Er kunnen onderliggende factoren zijn die bijdragen aan een complexe variabele, zoals een taalscore. Zelfs als de ene variabele in verband staat met de andere, kan dit verband worden veroorzaakt door een derde, onderliggende variabele. Ook kunnen er slechts indirecte verbanden tussen de variabelen bestaan.
Een grote steekproef kan de statistische significantie van een correlatiecoëfficiënt sterk beïnvloeden, omdat kleine correlatiecoëfficiënten bij een grote steekproef significant kunnen lijken.
Effectgrootte
Een statistisch significant resultaat betekent niet per se dat er belangrijke toepassingen zijn in het echte leven of in een klinische setting.
De effectgrootte bepaalt hoe belangrijk de resultaten zijn voor de praktijk. Daarom is het van belang om effectgroottes te rapporteren voor een compleet beeld van je resultaten. Als je in de APA-stijl schrijft, rapporteer je ook intervalschattingen van de effectgrootte.
Cohen’s d blijkt gelijk te zijn aan 0.72, dus de effectgrootte is medium tot hoog.
Je waarde is tussen de 0.1 en 0.3, dus er is sprake van een heel klein effect. Dit betekent dat de gevonden relatie tussen ouderlijk inkomen en taalscores maar een beperkte praktische significantie heeft.
Type I- en Type II-fouten
Type I- en Type II-fouten hebben betrekking op fouten in je onderzoeksconclusies. Een Type I fout (type I error) betekent dat je de nulhypothese hebt verworpen, terwijl deze eigenlijk waar was. Een Type II-fout (type II error) betekent dat je de nulhypothese niet hebt verworpen, terwijl deze niet klopte.
Je kunt proberen het risico op deze fouten te minimaliseren door een goed significantieniveau te kiezen en voor een hoge power te zorgen. Er is echter wel een wisselwerking tussen de twee typen fouten: een kleiner risico op het ene type fout gaat gepaard met een groter risico op het andere type fout. Het is dus noodzakelijk om een balans te vinden.
Frequentistische versus Bayesiaanse statistiek
Bij frequentistische statistiek begin je altijd met de aanname dat de nulhypothese waar is, en draait de analyse om het toetsen van de nulhypothese.
Hoewel deze methode op dit moment nog steeds het vaakst wordt gebruikt, groeit Bayesiaanse statistiek in populariteit. Hierbij gebruik je eerder onderzoek om je hypothesen steeds te updaten (op basis van verwachtingen en observaties).
Bayes’ factor vergelijkt de relatieve sterkte van het bewijs voor de nulhypothese met de alternatieve hypothese. Hierbij trek je geen eindconclusie waarbij je de nulhypothese wel of niet verwerpt.
Rapporteren van statistische resultaten
In het Nederlands gebruiken we komma’s om de scheiding tussen hele getallen en decimalen aan te geven, en punten voor duizendtallen. Bij een rapportage van statistische resultaten is het vaak gebruikelijker om punten te gebruiken als decimaalteken, zeker als je volgens de APA-richtlijnen werkt.
Een voordeel van de punt is dat je bij statistische rapportages vaak getallen van elkaar moet scheiden met een komma. Door een punt te gebruiken als decimaalteken, wordt de tekst minder verwarrend.