Hoe bereken je de mediaan (median)? | Stappenplan & Voorbeelden

De mediaan (median) is de waarde die zich precies in het midden van een dataset bevindt als je de waarden van laag naar hoog zet. Het is een centrummaat die de laagste 50% van de waarden scheidt van de hoogste 50%.

De stappen om de mediaan te vinden zijn afhankelijk van het aantal waarden in de dataset. Bij een oneven aantal staat één waarde in het midden, maar bij een even aantal waarden moet je het gemiddelde van de twee middelste waarden berekenen om de mediaan te vinden.

De mediaan wordt meestal gebruikt voor kwantitatieve data (waarbij de waarden numeriek zijn), maar je kunt de mediaan soms ook gebruiken voor ordinale data (waarbij de waarden zijn verdeeld over categorieën).

Mediaan berekenen

Je kunt de mediaan met de hand berekenen of met behulp van onze mediaan rekenmachine hieronder.

Ontvang feedback op taal, structuur, lay-out en bronvermelding

Professionele Scribbr-editors kijken je scriptie na op:

• Academisch taalgebruik
• Onduidelijke zinnen
• Grammaticale fouten
• Interpunctie
• Verboden woorden

Bekijk het voorbeeld

De mediaan bepalen bij een oneven aantal waarden

We lichten de stappen toe met een voorbeeld over de wekelijkse salarisuitbetaling van 5 studenten.

Stap 1: Zet de waarden van laag naar hoog

Stap 2: Bepaal de middelste positie

Gebruik de formule , waarbij n gelijk is aan het aantal waarden in je dataset.

Formule	Berekening

De mediaan is de waarde op de derde positie.

Stap 3: Zoek de waarde op de middelste positie

De mediaan voor deze dataset is 350 euro.

De mediaan bepalen bij een even aantal waarden

In een dataset met een even aantal waarden is er geen sprake van een midden. Er staan namelijk twee waarden op de middelste positie. Daarom moet je de procedure om de mediaan te vinden iets aanpassen.

We voegen nog een waarde toe aan de dataset, zodat we 6 waarden (een even aantal) hebben.

Stap 1: Zet de waarden van laag naar hoog

Stap 2: Bepaal de twee middelste posities

Je vindt de middelste posities met behulp van de formules en , waarbij n gelijk is aan het aantal waarden in je dataset.

Formule	Berekening

De middelste waarden staan op de derde en vierde positie.

Stap 3: Zoek de twee waarden op de middelste posities

De middelste waarden zijn 350 en 500.

Stap 4: Bereken het gemiddelde van de twee middelste waarden

Je kunt de mediaan vinden door het gemiddelde te berekenen. Dit doe je door de twee middelste waarden bij elkaar op te tellen en dit getal door twee te delen.

Mediaan:

De mediaan voor deze dataset is 425 euro.

De mediaan bepalen voor ordinale data

De mediaan wordt meestal gebruikt voor kwantitatieve data, wat betekent dat de waarden numeriek zijn. Soms is het ook mogelijk om de mediaan te bepalen voor ordinale data.

Ordinale data kunnen worden verdeeld over categorieën met een rangorde. Een voorbeeld van een ordinale variabele is iemands taalvaardigheid (beginner, gemiddeld, gevorderd) of de mate van overeenstemming (oneens, neutraal, eens).

Het proces om de mediaan te vinden is bijna hetzelfde als voor kwantitatieve data.

Dataset met een oneven aantal waarden

We gebruiken een dataset met 7 waarden (oneven aantal) om de stappen te doorlopen

Je categoriseert reactietijden van participanten met behulp van drie groepen: langzaam, gemiddeld en snel.

Allereerst zet je alle waarden op volgorde van laag naar hoog.

Vervolgens bepaal je de middelste waarde met de formule , waarbij n gelijk is aan het aantal waarden in de dataset.

Formule	Berekening

De mediaan is de waarde op de vierde positie.

De mediaan voor deze dataset is gemiddeld.

Kun je de mediaan vinden voor ordinale datasets met een even aantal waarden?

Het is niet mogelijk om het gemiddelde te berekenen voor ordinale data, dus de mediaan kan niet worden bepaald voor een dataset met een even aantal nummers.

Als de twee middelste waarden bijvoorbeeld “langzaam” en “gemiddeld” zijn, kun je het gemiddelde niet vinden, omdat ze niet bij elkaar kunnen worden opgeteld en ook niet kunnen worden gedeeld door 2.

In de praktijk worden ordinale data soms omgezet naar een numeriek systeem, waarna ze behandeld worden als kwantitatieve data. Op die manier kan het gemiddelde worden berekend om de mediaan te vinden.

Toch wordt dit enkel in sommige contexten als acceptabel beschouwd. In de meeste gevallen kun je de ordinale data niet zomaar behandelen als kwantitatieve data.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Wanneer gebruik je de mediaan?

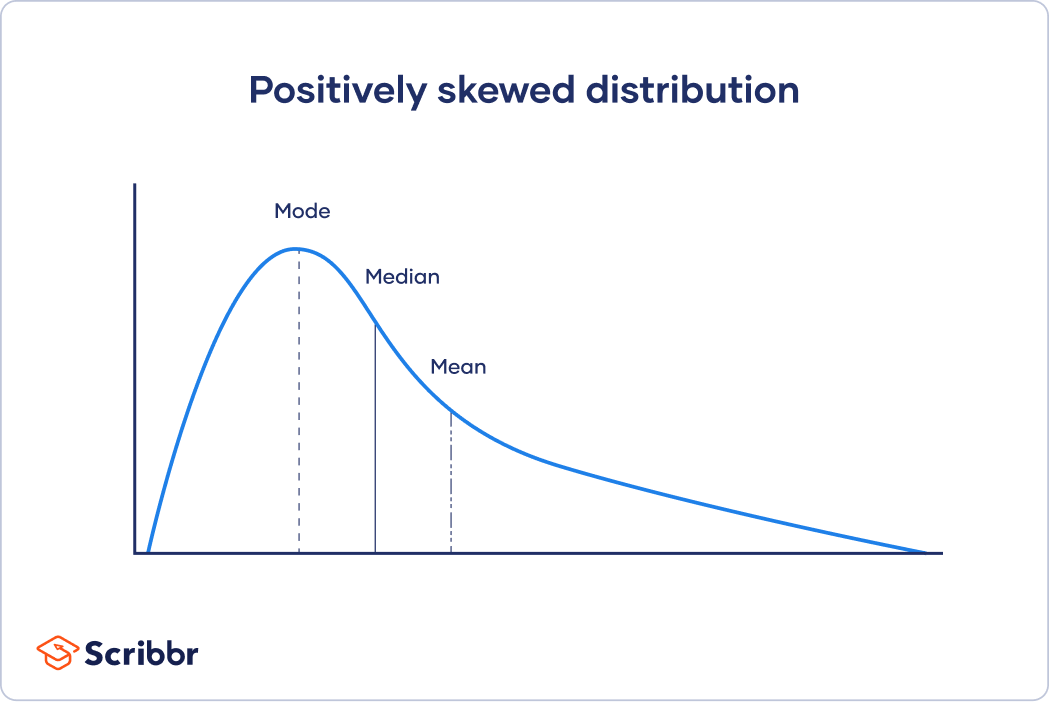
De mediaan is de meest informatieve centrummaat voor een dataset die niet normaal verdeeld is, zoals scheve verdelingen of verdelingen met uitbijters (ook wel uitschieters of outliers genoemd).

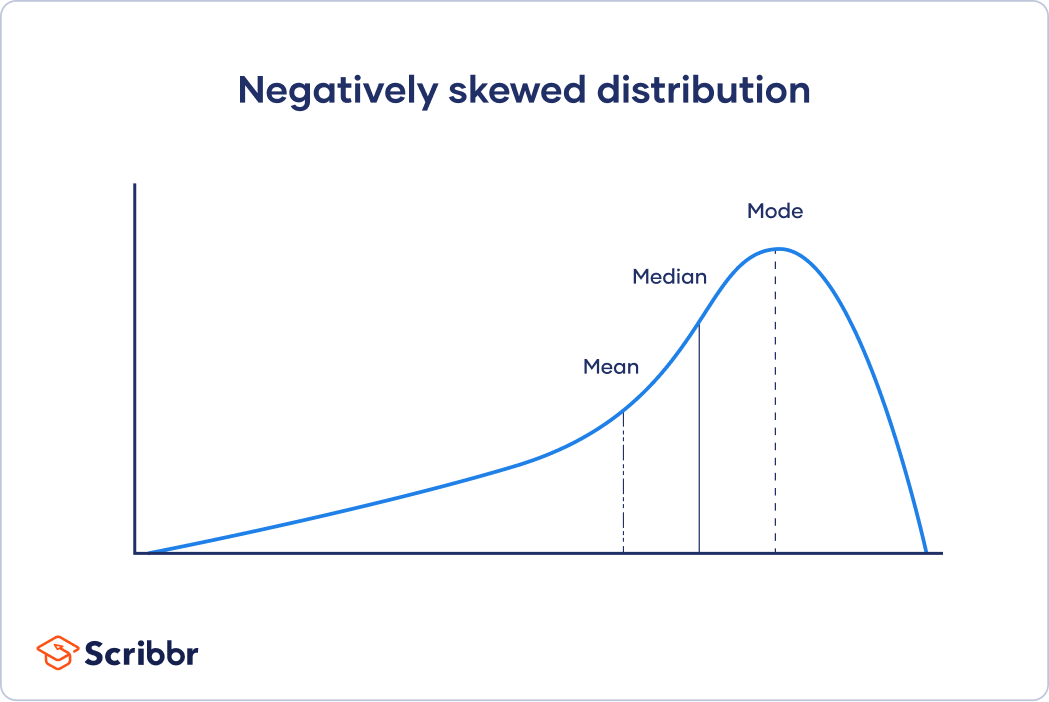
Bij scheve verdelingen bevinden zich meer waarden aan de ene kant van het centrum dan aan de andere kant. Het gemiddelde, de mediaan en de modus hebben alle drie een andere waarde.

In het geval van een rechtsscheve (positief-scheve verdeling) is er een cluster van lagere scores en een platte staart aan de rechterkant.

In het geval van een linksscheve (negatief-scheve) verdeling, is er een cluster van hogere scores en een platte staart aan de linkerkant.

Aangezien je voor de mediaan slechts één of twee waarden uit het midden van een dataset gebruikt, wordt deze maat niet beïnvloed door extreme uitbijters of niet-symmetrische verdelingen. Het gemiddelde en de modus kunnen wel sterk worden beïnvloed.

Daarom wordt de mediaan vaak gerapporteerd als centrummaat voor variabelen als “inkomen”, omdat deze verdelingen meestal rechtsscheef zijn.

Het meetniveau van je variabele bepaalt ook of je de mediaan mag gebruiken. De mediaan kan namelijk alleen worden gebruikt voor data die kunnen worden gerangschikt. Daarom kan de mediaan niet worden bepaald voor nominale data, maar wel voor ordinale data, intervaldata en ratiodata.

Veelgestelde vragen

Hoe vind je de mediaan?

Om de mediaan te vinden, zet je de waarden in je dataset van laag naar hoog. Vervolgens bepaal je de middelste positie op basis van n (het aantal waarden in je dataset).

• Als n een oneven getal is, vind je de mediaan op positie .
• Als n een even getal is, is de mediaan het gemiddelde van de waarden op posities en .

Wanneer gebruik je de mediaan als centrummaat?

De mediaan is de meest informatieve centrummaat voor scheve verdelingen of verdelingen met uitbijters. De mediaan wordt bijvoorbeeld vaak gebruikt als centrummaat voor de variabele “inkomen”, die over het algemeen niet normaal verdeeld is.

Aangezien je voor de mediaan slechts één of twee waarden in het midden gebruikt, wordt deze maat niet beïnvloed door extreme uitbijters of niet-symmetrische verdelingen. Het gemiddelde en de modus zijn hier wel gevoelig voor.

Wat zijn centrummaten (measures of central tendency)?

Centrummaten (measures of central tendency) helpen je het centrum of midden van een dataset te vinden.

De drie meest gebruikte centrummaten zijn het gemiddelde, de mediaan en de modus.

• De modus is de waarde die het vaakst voorkomt
• De mediaan is de middelste waarde als je de dataset van kleinste naar grootste waarde rangschikt.
• Het gemiddelde is de som van alle waarden, gedeeld door het totale aantal waarden.

Welke centrummaten kan ik gebruiken met mijn data?

Welke centrummaten je kunt gebruiken, is afhankelijk van het meetniveau en de verdeling van je data.

• Voor nominale data, kun je alleen de modus gebruiken om de meest voorkomende waarde te vinden.
• Voor ordinale data kun je zowel de modus en de mediaan gebruiken.
• Voor interval- of ratiodata kun je, naast de modus en mediaan, ook het gemiddelde gebruiken.

Ook moet je op de verdeling van je data letten. Voor normaal verdeelde data kun je alle drie de centrummaten gebruiken, maar bij scheve verdelingen is de mediaan de beste keuze.

Hoe kun je het gemiddelde berekenen?

Je kunt het gemiddelde van een dataset vinden door de volgende twee stappen te volgen:

1. Bereken de som door alle waarden bij elkaar op te tellen.
2. Deel de som door het aantal waarden in de dataset.

Deze methode werkt zowel voor steekproef- als populatiedata. Ook maakt het niet uit of je te maken hebt met positieve (+2) of negatieve waarden (-2).