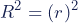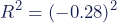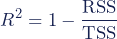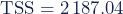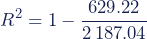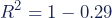Laat je scriptie nakijken op taal

Scriptie nakijkservice

Check je scriptie gratis op plagiaat

Plagiaat Checker

Literatuurlijst genereren volgens de APA-stijl

Bronnengenerator
  1. Home
  2. Knowledge Base
  3. Statistiek
  4. Coefficient of Determination (R²) | Betekenis & Voorbeelden

Coefficient of Determination (R²) | Betekenis & Voorbeelden

Vertaald op 5 juli 2022 door Veronique Scharwächter. Oorspronkelijk gepubliceerd door Shaun Turney

De determinatiecoëfficiënt (coefficient of determination) is een getal tussen de 0 en 1 dat de mate aanduidt waarin een statistisch model in staat is een bepaalde uitkomst te voorspellen.

Determinatiecoëfficiënt (R²) Interpretatie
0 Het model voorspelt de uitkomst niet.
Tussen 0 en 1 Het model voorspelt de uitkomst gedeeltelijk.
1 Het model voorspelt de uitkomst volledig.

De determinatiecoëfficiënt wordt meestal aangeduid met R², wat wordt uitgesproken als “r-kwadraat”. Bij een enkelvoudige lineaire regressie wordt in plaats van R² vaak een kleine letter r gebruikt (r²).

Wat is de determinatiecoëfficiënt?

De determinatiecoëfficiënt of coefficient of determination (R²) meet in hoeverre een statistisch model in staat is een bepaalde uitkomst te voorspellen. De uitkomst wordt gerepresenteerd door de afhankelijke variabele van het model.

De laagst mogelijke waarde van R² is 0 en de hoogst mogelijke waarde is 1. In het kort gezegd: hoe beter een model is in het maken van voorspellingen, hoe dichter de determinatiecoëfficiënt R² bij het getal 1 zal liggen.

R² is een maatstaf voor de aansluiting van het model bij de daadwerkelijke uitkomst (goodness of fit). Het is de proportie (het deel) van variantie in de afhankelijke variabele die wordt verklaard door het model.

Voorbeeld: Determinatiecoëfficiënt
Stel je voor dat je een enkelvoudige lineaire regressie uitvoert die de examencijfers van studenten voorspelt (de afhankelijke variabele) op basis van de tijd die ze studeren voor het examen (de onafhankelijke variabele).

  • Als de R² gelijk is aan 0, dan is het lineaire regressiemodel niet in staat om de examencijfers beter te voorspellen dan simpelweg te schatten dat iedereen een gemiddeld examencijfer heeft behaald.
  • Als de R² tussen de 0 en 1 ligt, kan het model de examencijfers gedeeltelijk voorspellen. De voorspellingen van het model zijn niet perfect, maar in ieder geval beter dan wanneer je enkel het gemiddelde examencijfer zou gebruiken.
  • Als de R² gelijk is aan 1, kun je het model gebruiken om de examencijfers van iedereen perfect te voorspellen.

Als je de data van je lineaire regressie in een grafiek zet, kun je hieruit meestal afleiden of de R² hoog of laag is. De onderstaande grafieken zijn gebaseerd op voorbeelddata:

  • De observaties worden weergegeven als stippen.
  • De voorspellingen van het model (de lijn van de beste pasvorm) worden getoond als een zwarte lijn.
  • De afstand tussen de daadwerkelijke observaties en hun voorspelde waarde (de residuen) worden weergegeven als paarse lijnen.

Je kunt in de eerste dataset zien dat R² hoog is, en dat de observaties dan dicht bij de voorspellingen van het model liggen. In andere woorden: de meeste stippen liggen dicht bij de zwarte lijn:

Determinatiecoëfficiënt (R²) = 0.9

Let op
De determinatiecoëfficiënt is altijd positief, zelfs als de correlatie negatief is.

Bij de tweede dataset kun je zien dat de R² laag is, en dat de observaties ver van de voorspellingen van het model verwijderd zijn. In andere woorden: de meeste stippen liggen ver van de zwarte lijn af:

Determinatiecoëfficiënt (R²) = 0.2

Ontvang feedback op taal, structuur, lay-out en bronvermelding

Professionele Scribbr-editors kijken je scriptie na op:

  • Academisch taalgebruik
  • Onduidelijke zinnen
  • Grammaticale fouten
  • Interpunctie
  • Verboden woorden

Bekijk het voorbeeld

De determinatiecoëfficiënt berekenen

Je kunt kiezen tussen twee formules om de determinatiecoëfficiënt (R²) van een enkelvoudige lineaire regressie te berekenen.

  • De eerste formule is specifiek voor eenvoudige lineaire regressies
  • De tweede formule kan worden gebruikt om de R² van veel verschillende typen statistische modellen te berekenen.

Formule 1: De correlatiecoëfficiënt gebruiken

Formule 1

    \begin{equation*}R^2=(r)^2\end{equation*}

Waarbij r = de Pearson correlatiecoëfficiënt.

Voorbeeld: R² berekenen met gebruik van de correlatiecoëfficiënt
Je onderzoekt de relatie tussen de hartslag en leeftijd bij kinderen, en je ontdekt dat de twee variabelen een negatieve Pearson correlatie hebben:

    \begin{equation*}r=-0.28\end{equation*}

Deze waarde kan worden gebruikt om aan de hand van Formule 1 de determinatiecoëfficiënt (R²) te berekenen:

    \begin{equation*}R^2=(r)^2\end{equation*}

    \begin{equation*}R^2=(-0.28)^2\end{equation*}

    \begin{equation*}R^2=0.08\end{equation*}

Formule 2: De regressieresultaten gebruiken

Formule 2

    \begin{equation*}R^2=1-\dfrac{\textup{RSS}}{\textup{TSS}}\end{equation*}

Waarbij:

  • RSS = som van de gekwadrateerde residuen (residual sum of squares) 
  • TSS = totale kwadratensom (total sum of squares)
Voorbeeld: R² berekenen met gebruik van de regressieresultaten
Als onderdeel van een enkelvoudige lineaire regressieanalyse waarin de examencijfers van studenten (afhankelijke variabele) worden voorspeld op basis van hun studietijd (onafhankelijke variabele), bereken je dat:

    \begin{equation*}\textup{RSS}=629.22\end{equation*}

    \begin{equation*}\textup{TSS}=2\,187.04\end{equation*}

Deze waarden kunnen worden gebruikt om aan de hand van Formule 2 de determinatiecoëfficiënt (R²) te berekenen:

    \begin{equation*}R^2=1-\dfrac{\textup{RSS}}{\textup{TSS}}\end{equation*}

    \begin{equation*}R^2=1-\dfrac{629.22}{2\,187.04}\end{equation*}

    \begin{equation*}R^2=1-0.29\end{equation*}

    \begin{equation*}R^2=0.71\end{equation*}

Determinatiecoëfficiënt interpreteren

Je kunt de determinatiecoëfficiënt (R²) interpreteren als de proportie van de variantie in de afhankelijke variabele die het statistisch model voorspelt.

Een andere manier om erover na te denken is dat de R² het deel van de variantie is dat de afhankelijke en onafhankelijke variabelen met elkaar delen.

Je kunt ook zeggen dat de R² de proportie van de variantie is die wordt “verklaard” of “verantwoord” door het statistisch model. Het deel dat overblijft (1 – R²) is dan de variantie die niet wordt verklaard door het model.

Tip
Als je wilt, kun je er ook voor kiezen om de R² te noteren als een percentage in plaats van een proportie. Dit doe je door de proportie te vermenigvuldigen met 100.

R² als effectgrootte

Als laatste zou je de R² ook kunnen interpreteren als een effectgrootte: dit is een maat voor de sterkte van de relatie tussen de afhankelijke en onafhankelijke variabelen. Psycholoog en statisticus Jacob Cohen (1988) heeft de volgende vuistregels opgesteld voor enkelvoudige lineaire regressies:

Minimale waarde van determinatiecoëfficiënt (R²) Interpretatie effectgrootte
.01 Klein
.09 Medium of middelgroot
.25 Groot

Let op: de R² op zichzelf zegt niets over een oorzakelijk verband.

Voorbeeld: R² interpreteren
Een enkelvoudige lineaire regressie die de examencijfers van studenten (afhankelijke variabele) voorspelt aan de hand van de studietijd (onafhankelijke variabele) heeft een R² van .71. Deze R²-waarde vertelt ons dat:

  •  71% van de variantie in de examencijfers van de studenten kan worden voorspeld op basis van hun studietijd.
  •  29% van de variantie in de examencijfers van de studenten wordt niet verklaard door het model.
  • De tijd die de studenten studeren voor het examen heeft een groot effect op hun examencijfers.

Langer studeren kan mogelijk de oorzaak zijn van een verbetering in de cijfers van de studenten. Hoewel een causale relatie hier erg aannemelijk is, is de R² alleen niet in staat om ons te vertellen waarom er een relatie bestaat tussen de studietijd en de examencijfers van de studenten.

Studenten zouden studeren bijvoorbeeld ook minder frustrerend kunnen vinden als ze het lesmateriaal beter begrijpen, en daarom langer studeren.

Determinatiecoëfficiënt rapporteren

Als je besluit om de determinatiecoëfficiënt (R²) te gebruiken in je paper of scriptie, dien je deze te rapporteren in je onderzoeksresultaten. Je kunt de volgende regels gebruiken om statistieken te rapporteren in APA-stijl:

  • Gebruik “r²” voor statistische modellen met één onafhankelijke variabele (zoals enkelvoudige lineaire regressies). Gebruik “R²” voor statistische modellen met meerdere onafhankelijke variabelen.
  • Het is niet nodig om een referentie of formule toe te voegen, aangezien de determinatiecoëfficiënt een veelgebruikte statistiek is.
  • Cursiveer r² en R² wanneer je hun waarden rapporteert (maar cursiveer de 2 niet).
  • Voeg nooit een voorloopnul toe (een nul voor de decimale punt), want de determinatiecoëfficiënt kan niet groter zijn dan 1.
  • Achter de decimale punt dienen twee significante getallen te staan.
  • De determinatiecoëfficiënt wordt meestal gerapporteerd in combinatie met gerelateerde statistische resultaten, zoals de F-waarde, de vrijheidsgraden, en de p-waarde.
Voorbeeld: Rapporteer r² in APA-stijl
De examencijfers van studenten zijn voorspeld aan de hand van hun studietijd, r² = .71, F(1,32) = 7.33, p = .003

Lees waarom zo veel studenten Scribbr inschakelen

Trustpilot

Ontdek nakijken op taal

Valkuil van de determinatiecoëfficiënt

Een belangrijke valkuil van de determinatiecoëfficiënt (R²) is dat een hoge of lage R² lijkt te bepalen of een model goed of slecht is. Dit is echter niet waar.

Als je in een lineaire regressieanalyse meer onafhankelijke variabelen toevoegt om de afhankelijke variabele te verklaren, zal de determinatiecoëfficiënt (R²) altijd toenemen, ook als de onafhankelijke variabelen helemaal geen verband houden met de afhankelijke variabele.

Dit komt doordat de determinatiecoëfficiënt het deel van de variantie in de afhankelijke variabele weergeeft dat wordt voorspeld door het model. Hoe meer onafhankelijke variabelen je toevoegt, hoe meer variantie er verklaard lijkt te worden.

Hierdoor kan de mate van verklaarbaarheid van het model overschat worden.

Daarom is de aangepaste determinatiecoëfficiënt (R2) ontwikkeld, die aantoont welk deel van de variantie in de afhankelijke variabele door alle onafhankelijke variabelen gezamenlijk wordt voorspeld door het model.

Oefenvragen over de coefficient of determination

Veelgestelde vragen over de coefficient of determination

Wat is de definitie van de determinatiecoëfficiënt (R²)?

De determinatiecoëfficiënt (R²) is een getal tussen de 0 en 1 dat de mate aanduidt waarin een statistisch model in staat is een bepaalde uitkomst te voorspellen. Je kunt de R² interpreteren als de proportie (het deel) van de variantie in de afhankelijke variabele die wordt voorspeld door het statistisch model.

Wat is de formule voor de determinatiecoëfficiënt?

Er zijn twee formules die je kan gebruiken om de determinatiecoëfficiënt (R²) van een enkelvoudige lineaire regressie te berekenen.

Formule 1: R^2=(r)^2

Formule 2: R^2=1-\dfrac{\textup{RSS}}{\textup{TSS}}

Hoe bereken ik de determinatiecoëfficiënt (R²) in softwareprogramma R?

Je kunt de samenvattingsfunctie() (ook wel summary () function) gebruiken om R² (coefficient of determination) van een lineair model weer te geven in R. Onderaan de output zie je “R-kwadraat” (“R-squared”) staan.

Hoe bereken ik de determinatiecoëfficiënt (R²) in Excel?

Je kunt de RSQ() functie gebruiken om R² (coefficient of determination) in Excel te berekenen. Als je afhankelijke variabele in kolom A staat, en je onafhankelijke variabele in kolom B, klik je op een willekeurige lege cel en typ je: “RSQ(A:A,B:B)”.

Wat is de coefficient of determination?

De coefficient of determination is de Engelse term voor de determinatiecoëfficiënt.

De determinatiecoëfficiënt (R²) is een getal tussen de 0 en 1 dat de mate aanduidt waarin een statistisch model in staat is een bepaalde uitkomst te voorspellen.

Citeer dit Scribbr-artikel

Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.

Scharwächter, V. (2022, 05 juli). Coefficient of Determination (R²) | Betekenis & Voorbeelden. Scribbr. Geraadpleegd op 11 november 2024, van https://www.scribbr.nl/statistiek/determinatiecoefficient/

Citeer dit artikel
Wat vind jij van dit artikel?
Veronique Scharwächter

Veronique heeft twee bachelors: één in Taal- en Cultuurstudies en één in Philosophy, Politics and Economics. Daarnaast heeft zij een boek geschreven over hoe filosofie je kan helpen in je studentenleven. Ze hoopt haar brede, interdisciplinaire kennis in te kunnen zetten om zo veel mogelijk studenten te helpen met het schrijven van hun scriptie.

Andere studenten bekeken ook

Regressieanalyse uitvoeren en interpreteren

Een regressieanalyse probeert de samenhang tussen variabelen uit te drukken in een vergelijking. Bekijk hoe je deze uitvoert en interpreteert.
322 Leestijd: 5 min.

Wat is de effectgrootte en waarom is deze van belang?

De effectgrootte laat zien hoe betekenisvol de relatie tussen variabelen of het verschil tussen groepen is (praktische relevantie).
16 Leestijd: 5 min.

Variantie begrijpen en berekenen | Uitleg met voorbeelden

De variantie zegt iets over de spreiding in een dataset. Hoe meer de data verspreid zijn, hoe groter de variantie.
25 Leestijd: 5 min.