Ratiodata verzamelen & analyseren | Met voorbeelden

Een ratioschaal is een kwantitatieve schaal met een betekenisvol of absoluut nulpunt en gelijke intervallen tussen aangrenzende punten. Het betekenisvolle nulpunt betekent dat bij de waarde “0” de variabele daadwerkelijk afwezig is.

Voorbeelden van ratioschalen zijn lengte, oppervlakte en bevolkingsaantallen.

Meetniveaus

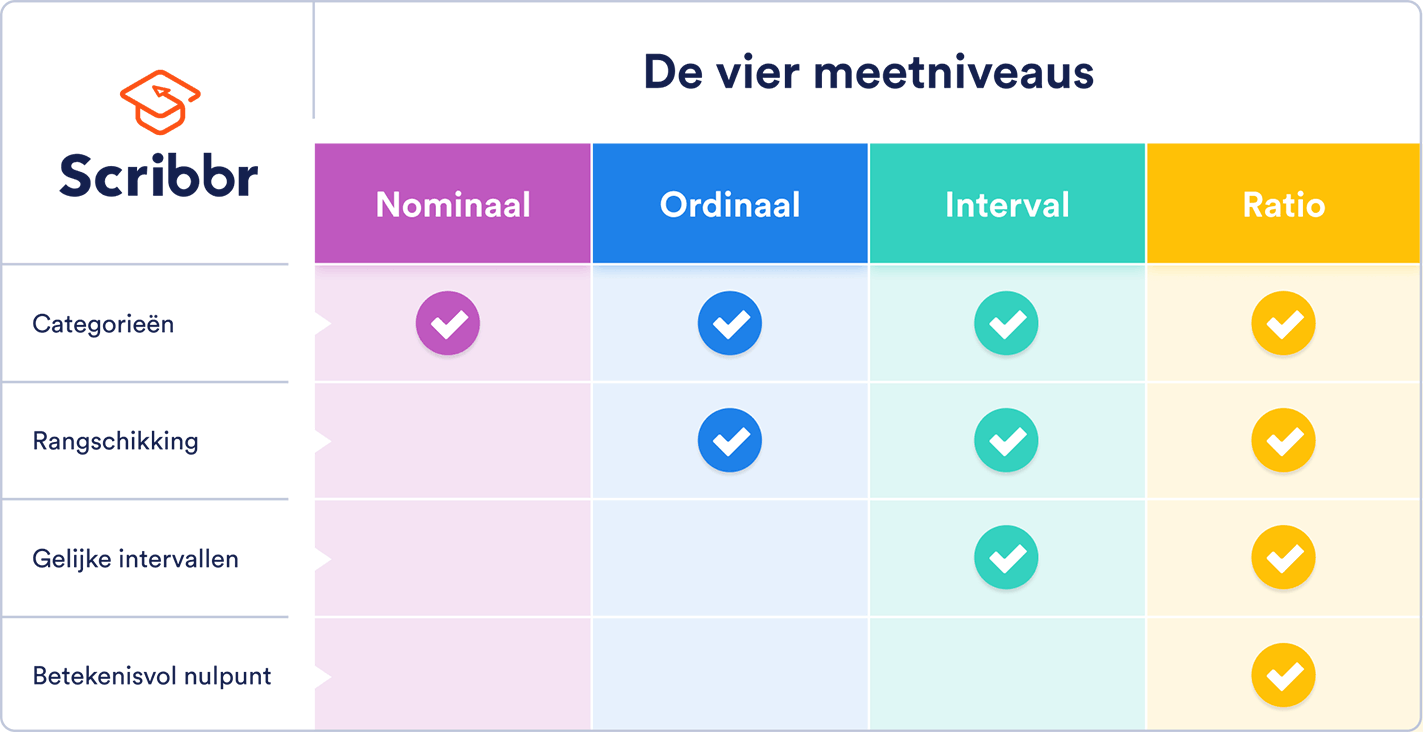
Het meetniveau geeft aan hoe precies de data zijn verzameld. Er zijn vier meetniveaus: nominaal, ordinaal, interval en ratio. Een hoger meetniveau is altijd complexer en preciezer, en daarom is ratio het meest precieze en complexe niveau.

Data op rationiveau hebben alle kenmerken van de andere drie niveaus. De waarden kunnen worden gecategoriseerd, geordend en de intervallen tussen twee aangrenzende waarden zijn gelijk. In tegenstelling tot intervaldata, is er bij ratiodata sprake van een betekenisvol nulpunt (true zero).

Nominale en ordinale variabelen behoren tot de categorische variabelen, terwijl interval– en ratiovariabelen kwantitatieve variabelen zijn. Deze twee typen noem je samen scale. Er kunnen veel meer statistische analyses worden uitgevoerd op kwantitatieve data dan op categorische data.

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

Wat is een betekenisvol of absoluut nulpunt?

Op een ratioschaal betekent de waarde nul dat de relevante variabele totaal afwezig is. Stel dat je onderzoek doet naar het aantal kinderen in een huishouden of naar het aantal jaren werkervaring, dan kan het voorkomen dat een participant geen kinderen heeft of geen enkele werkervaring. In dat geval betekent nul dus ook echt nul.

Als een schaal een betekenisvol nulpunt heeft, kun je verhoudingen berekenen. Je kunt bijvoorbeeld zeggen dat 4 kinderen twee keer zoveel is als 2 kinderen. Ook kun je zeggen dat 8 jaar ervaring het dubbele van 4 jaar ervaring is.

Sommige variabelen, zoals temperatuur, kunnen op verschillende schalen worden gemeten. Zo zijn Celsius en Fahrenheit intervalschalen, omdat je ook nog min-temperaturen hebt. De intervallen tussen twee aangrenzende temperaturen, bijvoorbeeld 31 en 32 graden of 12 en 13 graden, zijn wel gelijk, maar er is geen absoluut, betekenisvol nulpunt.

De temperatuurschaal Kelvin heeft wel een absoluut nulpunt (0 K), omdat niets kouder kan zijn dan dat punt. Kelvin kent geen min-temperaturen. Dit betekent dat je alleen bij de Kelvin-temperatuurschaal met temperatuurverhoudingen kunt werken. Bijvoorbeeld:

• 40 K is twee keer zo heet als 20 K
• 40° C is niet twee keer zo heet als 20° C

Het absolute en betekenisvolle nulpunt maakt het mogelijk om de waarden te vermenigvuldigen, te delen of de kwadrateren. Het rationiveau heeft altijd de voorkeur (indien mogelijk), omdat je zo de meeste berekeningen kunt uitvoeren.

Voorbeelden van ratioschalen

Ratiovariabelen kunnen net als intervalvariabelen discreet of continu van aard zijn. Een discrete variabele wordt uitgedrukt in telbare, ronde (of hele) getallen (1, 2, 3, et cetera), terwijl een continue variabele elke waarde kan aannemen (bijvoorbeeld 1,59 en 4,5643).

Hoe analyseer je ratiodata?

Nadat je ratiodata hebt verzameld, kun je beschrijvende (descriptieve) en toetsende (inferentiële) statistieken verzamelen. In het geval van ratiodata kun je bijna alle statistische toetsen inzetten, omdat alle wiskundige bewerkingen zijn toegestaan.

Je kunt de volgende descriptieve statistieken verzamelen om je data samen te vatten:

• De frequentieverdeling in absolute getallen of percentages
• De modus, mediaan en het gemiddelde om de centrale tendens te vinden
• Het bereik, de standaarddeviatie en de variantie om de spreiding aan te geven

Verdeling (distribution)

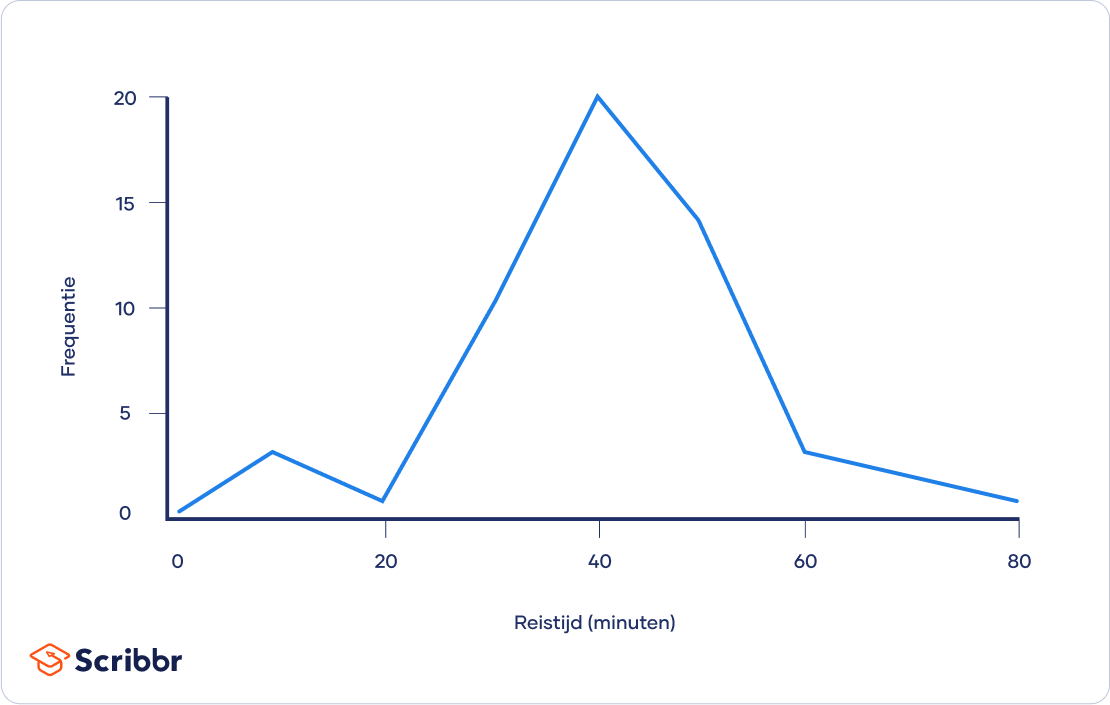
Je kunt een frequentieoverzicht maken met behulp van een tabel, om vervolgens de verdeling te visualiseren in een grafiek of diagram.

• Tabel
• Grafiek

Om je data te organiseren, vat je de waarden samen in een gegroepeerde frequentietabel. Zorg voor groepen met gelijke intervallen in de linkerkolom en plaats de frequenties in de rechterkolom.

Reistijd (minuten)	Frequentie
1 – 10	3
11 – 20	1
21 – 30	9
31 – 40	19
41 – 50	13
51 – 60	3
61 – 70	2
71 – 80	1

Om je data te visualiseren, zet je de waarden om in een grafiek. Je plaatst de groepen (intervallen) op de x-as en je plot de frequenties op de y-as. Hierdoor ontstaat een lijn door alle kruispunten van de x- en y-as.

Centrummaten (centrale tendens)

Aan de vorm van de grafieklijn kun je zien dat de gegevens bij benadering normaal verdeeld zijn. Daarom kun je zowel de modus (mode) als de mediaan (median) en het gemiddelde (mean) vaststellen om de centrale tendens te bepalen. De centrale tendens laat zien rond welke waarde de meeste waarden zich bevinden.

Het gemiddelde wordt meestal gezien als de beste maat voor de centrale tendens als de kwantitatieve data normaal verdeeld zijn. Dat komt doordat bij deze maat alle waarden uit de dataset worden meegenomen, in tegenstelling tot bij de modus of mediaan.

Spreidingsmaten (variability)

Het bereik (range), de standaarddeviatie (standard deviation) en de variantie (variance) laten de mate van spreiding zien. Het bereik is het makkelijkste om te berekenen, maar de standaarddeviatie en variantie geven meer waardevolle informatie.

Statistische toetsen

Nu je een overzicht hebt van de gegevens, kun je een geschikte statistische toets kiezen. Als de ratiodata normaal verdeeld zijn, kun je het beste een parametrische toets kiezen om je hypothese te toetsen.

Parametrische toetsen zijn krachtiger dan niet-parametrische toetsen, waardoor je betere conclusies kunt trekken over de gegevens. Je data moeten echter wel aan een aantal voorwaarden voldoen om parametrische toetsen te kunnen gebruiken.

De volgende parametrische toetsen worden het vaakst gebruikt om ratiodata te analyseren.

Ontvang feedback op taal, structuur, lay-out en bronvermelding

Professionele Scribbr-editors kijken je scriptie na op:

• Academisch taalgebruik
• Onduidelijke zinnen
• Grammaticale fouten
• Interpunctie
• Verboden woorden

Bekijk het voorbeeld

Veelgestelde vragen

Wat zijn de vier meetniveaus?

Meetniveaus laten zien hoe precies variabelen worden gemeten. Er zijn vier meetniveaus (of meetschalen) die van laag naar hoog kunnen worden gerangschikt.

• Nominaal: De data kunnen alleen worden gecategoriseerd (geen rangorde).
• Ordinaal: De data kunnen worden gecategoriseerd en gerangschikt.
• Interval: De data kunnen worden gecategoriseerd en gerangschikt en er zijn gelijke intervallen tussen de categorieën.
• Ratio: De data kunnen worden gecategoriseerd en gerangschikt, de intervallen zijn gelijk, en er is een absoluut of betekenisvol nulpunt.

Hoe bepaal ik welk meetniveau ik moet gebruiken?

Sommige variabelen gaan gepaard met een vaststaand meetniveau. Zo worden gender of etniciteit altijd op nominaal niveau gemeten, omdat je de categorieën niet kunt rangschikken.

Bij andere variabelen kun je het meetniveau wel kiezen. De variabele “studenteninkomen” kan bijvoorbeeld op ordinaal of rationiveau worden gemeten.

• Op ordinaal niveau zou je vijf groepen kunnen creëren met een bepaald bereik (bijvoorbeeld 0 – 499, 500 – 799, 800 – 1099, 1100 – 1999 en 2000 – 2299). Participanten kruisen dan het juiste bereik aan.
• Op rationiveau zou je naar het exacte inkomen vragen.

Als je kunt kiezen, is het beter om op rationiveau te meten, zodat je de data op meer manieren kunt analyseren. Hoe hoger je meetniveau, hoe preciezer de data.

Wat is het verschil tussen interval- en ratiodata?

Hoewel interval– en ratiodata beide kunnen worden gecategoriseerd, gerangschikt en gelijke afstanden hebben tussen aangrenzende waarden (gelijke intervallen), hebben alleen ratiodata een absoluut of betekenisvol nulpunt.

De temperatuur in Celsius of Fahrenheit is een voorbeeld van een intervalschaal, omdat nul niet de laagst mogelijke temperatuur is. Je kunt namelijk ook nog te maken hebben met min-temperaturen. Een Kelvin-temperatuurschaal is een voorbeeld van een ratioschaal, omdat nul het absolute nulpunt is. Er zijn geen min-temperaturen.