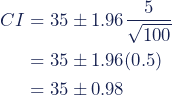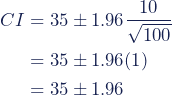Betrouwbaarheidsinterval Berekenen | Formules & Voorbeelden
Het betrouwbaarheidsinterval (confidence interval) is het waardebereik waarbinnen je geschatte waarde naar verwachting een bepaald percentage van de keren ligt als je het experiment of de steekproef hetzelfde zou herhalen.
Als je een schatting maakt in de statistiek (bijvoorbeeld voor een samenvattende of teststatistiek), is er altijd onzekerheid over die schatting omdat het getal gebaseerd is op een steekproef van de populatie die je bestudeert.
Inhoudsopgave
- Wat is een betrouwbaarheidsinterval?
- Betrouwbaarheidsinterval berekenen
- Betrouwbaarheidsinterval voor het gemiddelde van normaal verdeelde data
- Betrouwbaarheidsinterval voor proporties
- Betrouwbaarheidsinterval voor niet normaal verdeelde data
- Betrouwbaarheidsinterval rapporteren
- Valkuil van een betrouwbaarheidsinterval
- Veelgestelde vragen over betrouwbaarheidsintervallen berekenen
Wat is een betrouwbaarheidsinterval?
Een betrouwbaarheidsinterval is het gemiddelde van je schatting plus of min de variatie in die schatting. Dit is het bereik van waarden waartussen je verwacht dat je schatting zal vallen als je je test opnieuw doet, binnen een bepaald betrouwbaarheidsniveau.
Betrouwbaarheid is een andere manier om waarschijnlijkheid te beschrijven. Als je bijvoorbeeld een betrouwbaarheidsinterval met een betrouwbaarheidsniveau van 95% kiest, betekent dit dat je ervan overtuigd bent dat de schatting 95 van de 100 keer tussen de bovenste en onderste waarden van het betrouwbaarheidsinterval zal vallen.
Je gewenste betrouwbaarheidsniveau is normaal gesproken 1 min de alfawaarde (α) die je voor je statistische toets hebt gebruikt:
Betrouwbaarheidsniveau = 1 – α
Als je een alfawaarde van 0,05 gebruikt voor statistische significantie, dan is je betrouwbaarheidsniveau 1 – 0.05 = 0.95, of 95%.
Wanneer gebruik je een betrouwbaarheidsinterval?
Je kunt betrouwbaarheidsintervallen berekenen voor allerlei soorten statistische schattingen, waaronder:
- Proporties (verhoudingen)
- Populatiegemiddelden
- Verschillen tussen populatiegemiddelden en proporties
- Schattingen van de variatie tussen groepen
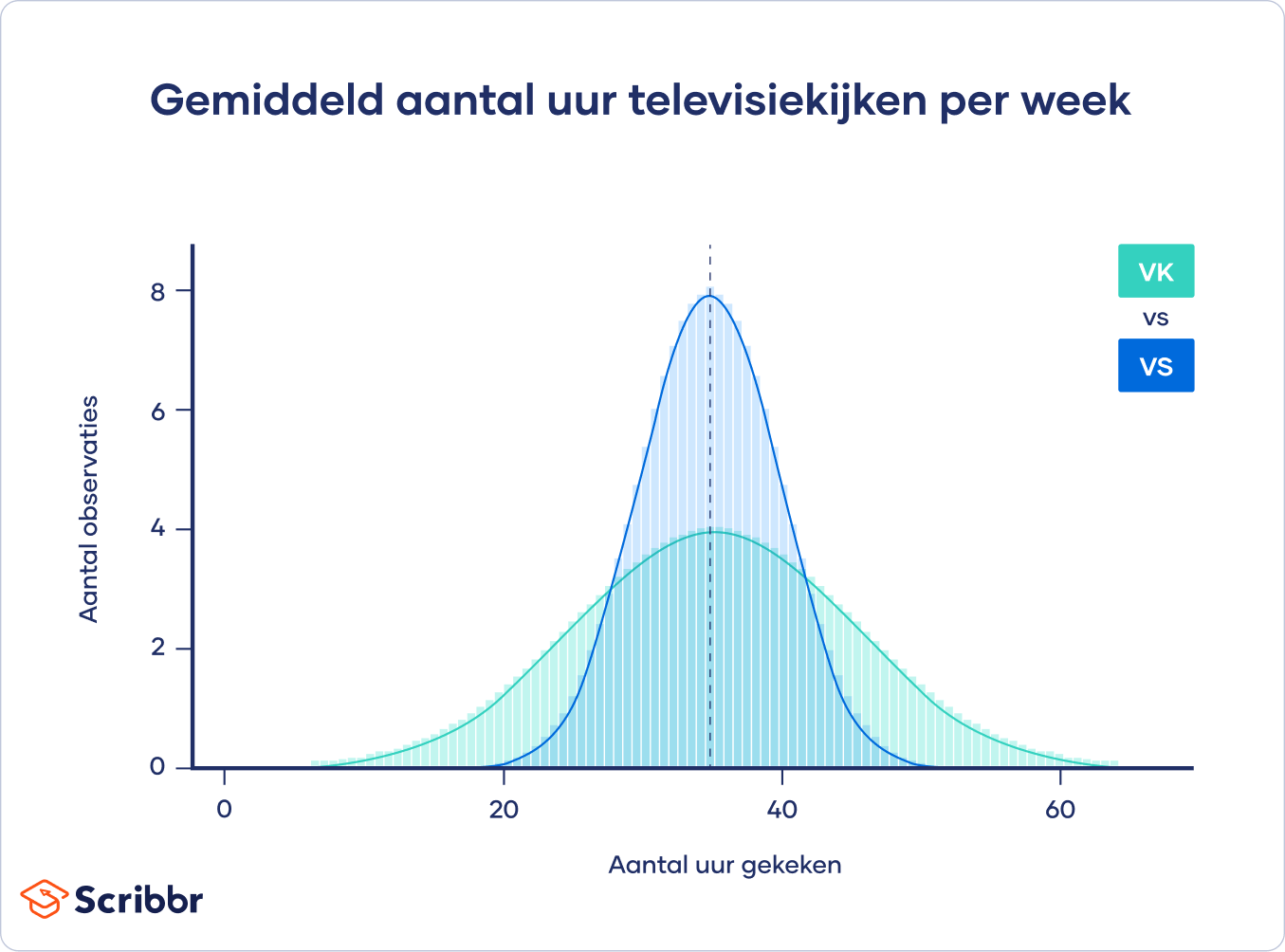
Dit zijn allemaal puntschattingen die geen informatie geven over de variatie rondom de waarde. Betrouwbaarheidsintervallen geven informatie over de variatie rondom een puntschatting.
Hoewel beide groepen dezelfde puntschatting hebben (het gemiddelde aantal uren televisiekijken), zal de Britse schatting een breder betrouwbaarheidsinterval hebben dan de Amerikaanse schatting omdat er meer variatie in de data zit.
Lees waarom zo veel studenten Scribbr inschakelen
Betrouwbaarheidsinterval berekenen
De meeste statistische programma’s zullen ook het betrouwbaarheidsinterval geven als je een statistische analyse uitvoert.
Als je zelf een betrouwbaarheidsinterval wilt berekenen, moet je het volgende weten:
- De puntschatting waarvoor je het betrouwbaarheidsinterval opstelt;
- De kritieke waarden voor de teststatistiek;
- De standaarddeviatie van de steekproef;
- De steekproefgrootte.
Zodra je deze dingen weet, kun je het betrouwbaarheidsinterval voor je schatting berekenen met de formule voor het betrouwbaarheidsinterval die geschikt is voor jouw data.
Puntschatting
De puntschatting van je betrouwbaarheidsinterval is de statistische schatting die je maakt (e.g., populatiegemiddelde, verschil tussen populatiegemiddelden, proporties, variatie tussen groepen).
De kritieke waarde bepalen
Kritieke waarden geven aan hoeveel standaarddeviaties je van het gemiddelde verwijderd moet zijn om het gewenste betrouwbaarheidsniveau van je betrouwbaarheidsinterval te bereiken.
Er zijn drie stappen om de kritieke waarde te vinden.
- Kies je alfawaarde α
De alfawaarde is de drempelwaarde voor statistische significantie. De meest gebruikte alfawaarde is 0.05, maar 0.1, 0.01 en 0.001 worden soms ook gebruikt. Je kunt het beste naar gepubliceerde artikelen uit je vakgebied kijken om te beslissen welke alfawaarde je gebruikt.
- Beslis of je een eenzijdig of tweezijdig interval nodig hebt
Waarschijnlijk wil je een tweezijdig interval gebruiken, tenzij je een eenzijdige t-test (one-tailed t-test) uitvoert. Voor een tweezijdig interval deel je je alfa door 2 om de alfawaarde voor de boven- en ondergrenzen te vinden.
- Zoek de kritieke waarde op die overeenkomt met je alfawaarde
Als je data normaal verdeeld zijn of als je een grote steekproef (n > 30) hebt die bij benadering normaal verdeeld is, kun je de z-verdeling gebruiken om je kritieke waarden te vinden.
Voor een z-statistiek worden de meest voorkomende waarden in onderstaande tabel weergeven:
| Betrouwbaarheidsniveau | 90% | 95% | 99% |
|---|---|---|---|
| Alfa voor eenzijdig BI | 0.1 | 0.05 | 0.01 |
| Alfa voor tweezijdig BI | 0.05 | 0.025 | 0.005 |
| z-statistiek | 1.64 | 1.96 | 2.57 |
Let op: BI = betrouwbaarheidsinterval (of CI = confidence interval in het Engels).
Als je een kleine dataset (n ≤ 30) gebruikt die bij benadering normaal verdeeld is, gebruik je de t-verdeling.
De t-verdeling volgt dezelfde vorm als de z-verdeling maar corrigeert voor kleine steekproefgroottes. Voor de t-verdeling moet je je vrijheidsgraden kennen (steekproefgrootte min 1).
Bekijk deze t-tabel om je t-statistiek te vinden. Het betrouwbaarheidsniveau en de p-waarden voor zowel eenzijdige als tweezijdige toetsen zijn toegevoegd, zodat je de benodigde waarde kunt vinden.
Voor normale verdelingen, zoals de t-verdeling en de z-verdeling, is de kritieke waarde aan beide kanten van het gemiddelde gelijk.
Voor een tweezijdig 95%-betrouwbaarheidsinterval is de alfawaarde 0.025. De kritieke waarde die met deze alfawaarde overeenkomt is 1.96.
Dit betekent dat je de boven- en ondergrens van het betrouwbaarheidsinterval op +1.96 en -1.96 standaardafwijkingen van het gemiddelde kunt vaststellen.
De standaarddeviatie bepalen
De meeste statistische programma’s zullen een functie hebben om de standaarddeviatie te berekenen. Om deze handmatig te berekenen, moet je eerst de steekproefvariantie weten en hiervan de vierkantswortel nemen.
- Vind de steekproefvariantie
De steekproefvariantie wordt gedefinieerd als de som van de gekwadrateerde verschillen van het gemiddelde, ook wel bekend als de gemiddelde kwadratische fout (mean-squared-error, of MSE):
Om de MSE te bepalen, trek je het steekproefgemiddelde af van elke waarde in de dataset, kwadrateer je het resulterende getal en deel je dat getal door n – 1 (steekproefgrootte min 1).
Vervolgens tel je al deze getallen bij elkaar op om de totale steekproefvariantie (s2) te krijgen. Voor grotere steekproeven is het het makkelijkst om dit in Excel te doen.
- Vind de standaarddeviatie
De standaarddeviatie van je schatting (s) is gelijk aan de vierkantswortel van de steekproefvariantie (s2):
- √100 = 10 voor de Britse schatting.
- √25 = 5 voor de Amerikaanse schatting.
Steekproefgrootte
De steekproefgrootte is het aantal observaties in je dataset.
Betrouwbaarheidsinterval voor het gemiddelde van normaal verdeelde data
Normaal verdeelde data vormen een klokvorm als ze op een grafiek worden uitgezet, met het steekproefgemiddelde in het midden en de rest van de data ongeveer gelijk verdeeld aan beide kanten van het gemiddelde.
Het betrouwbaarheidsinterval voor data die de standaardnormale verdeling volgen is:
Waarbij:
- CI = het betrouwbaarheidsinterval (confidence interval)
= het populatiegemiddelde
- Z*= de kritieke waarde van de z-verdeling
- σ = de standaarddeviatie van de populatie
= de vierkantswortel van de populatiegrootte
Het betrouwbaarheidsinterval voor de t-verdeling volgt dezelfde formule, maar je vervang Z* door t*.
In het echte leven weet je nooit de echte waarden voor de populatie (tenzij je een volledige populatie kunt onderzoeken). In plaats daarvan vervang je daarom de waarden van de populatie door de waarden van de steekproef, zodat de formule als volgt wordt:
Waarbij:
= het steekproefgemiddelde
- s = de standaarddeviatie van de steekproef
Om het 95%-betrouwbaarheidsinterval te berekenen, gebruik je de waarden voor de formule.
Voor Amerika:
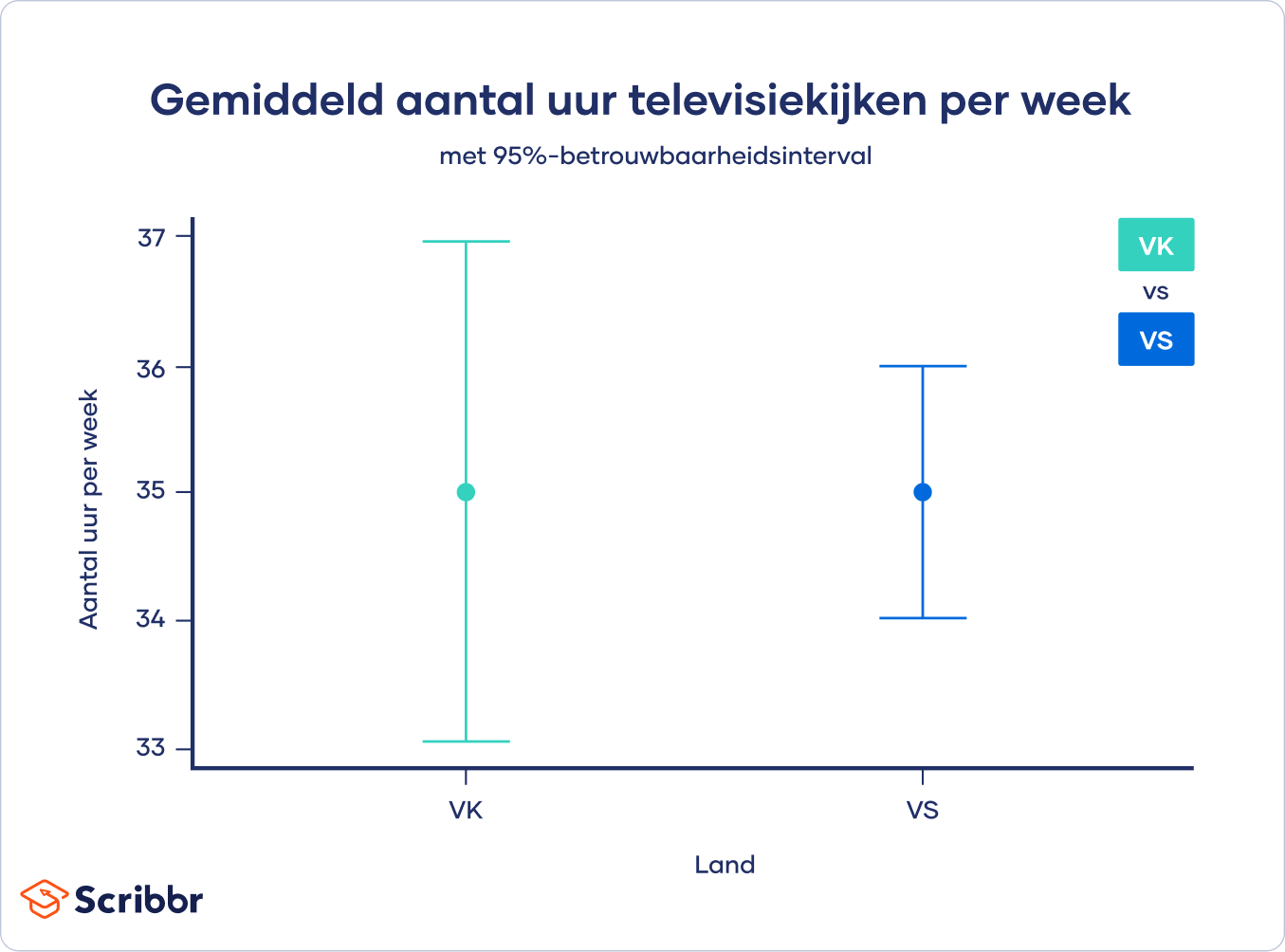
Voor Amerika zijn de boven- en ondergrens van het 95%-betrouwbaarheidsinterval 34.02 en 35.98.
Voor het Verenigd Koninkrijk:
Voor het Verenigd Koninkrijk zijn de boven- en ondergrens van het 95%-betrouwbaarheidsinterval 33.04 en 36.98.
Betrouwbaarheidsinterval voor proporties
Het betrouwbaarheidsinterval voor een proportie volgt hetzelfde patroon als het betrouwbaarheidsinterval voor gemiddelden, maar in plaats van de standaarddeviatie gebruik je de steekproefproportie en vermenigvuldig je deze met 1 min de proportie:
Waarbij:
= de proportie in je steekproef (e.g., het deel van respondenten dat aangaf überhaupt televisie te kijken)
- Z* = de kritieke waarde van de z-verdeling
- n = de steekproefgrootte
Lees waarom zo veel studenten Scribbr inschakelen
Betrouwbaarheidsinterval voor niet normaal verdeelde data
Als je het betrouwbaarheidsinterval rondom het gemiddelde van data die niet normaal verdeeld zijn wilt berekenen, heb je twee opties:
- Je kunt een verdeling vinden die overeenkomt met de vorm van je data en die verdeling gebruiken om je betrouwbaarheidsinterval te berekenen.
- Je kunt je data transformeren zodat ze bij een normale verdeling passen, en dan het betrouwbaarheidsinterval van de getransformeerde data vinden.
Datatransformaties zijn heel gebruikelijk in de statistiek, bijvoorbeeld als je data een logaritmische curve volgen maar je ze wilt gebruiken naast lineaire data. Je moet alleen niet vergeten om je data weer terug te transformeren als je de boven- en ondergrens van je betrouwbaarheidsinterval berekent.
Betrouwbaarheidsinterval rapporteren
Betrouwbaarheidsintervallen worden soms vermeld in onderzoekspapers, hoewel onderzoekers vaker de standaardafwijking van hun schatting rapporteren.
Als je het betrouwbaarheidsinterval wilt of moet rapporteren, is het belangrijk dat je de boven- en ondergrens van het betrouwbaarheidsinterval vermeld.
Betrouwbaarheidsintervallen worden vaak gebruikt in grafieken. Bij het weergeven van verschillen tussen groepen of bij het plotten van een lineaire regressie vermelden onderzoekers vaak het betrouwbaarheidsinterval om een de variatie rondom de schatting te visualiseren.
Valkuil van een betrouwbaarheidsinterval
Betrouwbaarheidsintervallen worden soms geïnterpreteerd als het waardebereik waarbinnen de “werkelijke waarde” van je schatting ligt.
Dit is niet het geval. Het betrouwbaarheidsinterval kan je niet vertellen hoe waarschijnlijk het is dat je de echte waarde van je schatting hebt gevonden, omdat de schatting gebaseerd is op de steekproef en niet op de hele populatie.
Het betrouwbaarheidsinterval vertelt je alleen binnen welk waardebereik je je waarde kan verwachten als je je steekproef opnieuw doet of je experiment op precies dezelfde manier uitvoert.
Hoe nauwkeuriger je steekproeftrekking of hoe realistischer je onderzoek, hoe groter de kans dat je betrouwbaarheidsinterval de werkelijke waarde van je schatting bevat. Maar deze nauwkeurigheid wordt dus bepaald door je onderzoeksmethoden en niet door de statistieken die je berekent nadat je je data hebt verzameld.
Veelgestelde vragen over betrouwbaarheidsintervallen berekenen
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Scharwächter, V. (2022, 13 juli). Betrouwbaarheidsinterval Berekenen | Formules & Voorbeelden. Scribbr. Geraadpleegd op 7 juli 2025, van https://www.scribbr.nl/statistiek/betrouwbaarheidsinterval/