Normale verdeling onderzoeken, begrijpen en interpreteren

De normale verdeling is een kansverdeling die beschrijft hoe data verspreid zijn. Normaal verdeelde data hebben de volgende eigenschappen:

• Observaties rond het gemiddelde zijn het waarschijnlijkst
• Hoe verder waardes van het gemiddelde af liggen, hoe onwaarschijnlijker het is deze waarden te observeren
• Waardes boven en onder het gemiddelde zijn even waarschijnlijk.

Wanneer is een normale verdeling belangrijk?

De aanname van een normale verdeling wordt bij veel statistische toetsen gemaakt. Bij het uitvoeren van een t-toets of anova is de aanname dat de data normaal verdeeld zijn. Bij een regressieanalyse nemen we aan dat fouttermen normaal verdeeld zijn.

De aanname van een normale verdeling is vooral belangrijk bij steekproeven kleiner dan 30 observaties. Bevat jouw steekproef meer dan 30 observaties dan kun je volgens de Centrale Limietstelling aannemen dat aan de aanname van normaliteit wordt voldaan.

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

Hoe ziet een normale verdeling eruit?

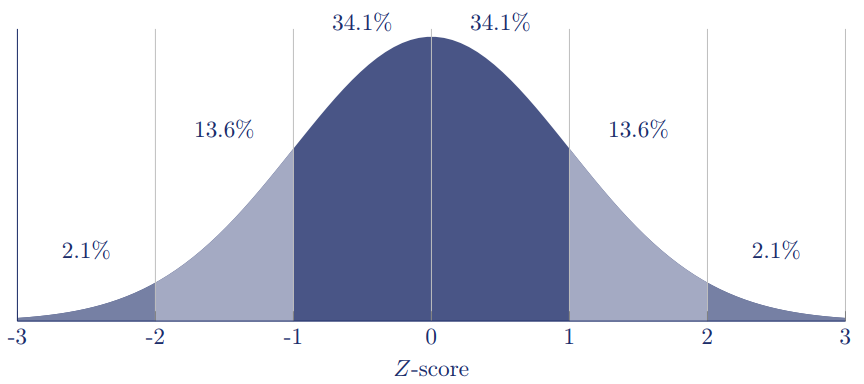
Er zijn twee parameters die bepalen hoe de normale verdeling eruitziet: het gemiddelde en de standaarddeviatie. Het onderstaande figuur laat zien wat de waarschijnlijkheid is voor observaties binnen drie standaarddeviaties van het gemiddelde.

Binnen één standaarddeviatie ligt 68,2% van de observaties (34,1% + 34,1%), binnen twee standaarddeviaties 95,2% en binnen drie standaarddeviaties 99,6%.

Voorbeeld van een normaal verdeelde variabele:
Stel dat de variabele SAT-score normaal verdeeld is met een gemiddelde van 1075 en een standaarddeviatie van 200. Een SAT-score van 200 punten boven het gemiddelde (1275) is dan even waarschijnlijk als het observeren van een score 200 punten onder het gemiddelde (875). De verwachting is dat 68% van de respondenten in steekproef tussen de 875 en 1275 scoort.

Testen voor normale verdeling met SPSS

Download het SPSS-bestand om met de data uit het voorbeeld te oefenen.

Om te onderzoeken of je variabele normaal verdeeld is, kun je in SPSS verschillende plots maken of statistische toetsen uitvoeren. Klik in de menubalk op:

• Analyze
• Descriptive Statistics
• Explore

In het scherm dat nu verschijnt, voeg je de variabele lengte toe aan de ‘dependent list’ en de variabele geslacht aan de ‘factor list’. Bij ‘Plots…’ vink je ‘Normality Plots with tests’ aan. Klik op Continue en vervolgens op OK om de normaliteitstoets uit te voeren.

In de output vind je de resultaten van de algemene Kolmogorov-Smirnov en de voor normaliteit specifieke Shapiro-Wilk-toets. De nulhypothese is dat de data normaal verdeeld zijn. Een significantie kleiner dan 0,05 duidt er dus op dat het onwaarschijnlijk is dat de data normaal verdeeld zijn. De Shapiro-Wilk-toets is over het algemeen strenger en kan dus het beste worden aangehouden.

Niet normaal verdeeld, wat nu?

Als je variabele niet normaal verdeeld is, kun je kijken of je de data kunt transformeren. Het kan namelijk zijn dat een variabele zelf niet normaal verdeeld is, maar het logaritme of het kwadraat wel. Wanneer ook dit niet het geval is, kun je niet-parametrische toetsen gebruiken zoals de Wilcoxon- of Mann-Whitney-toets in plaats van de t-toets.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Veelgestelde vragen

Waarom is het belangrijk dat je data normaal verdeeld zijn?

Veel statistische toetsen, zoals een t-toets of ANOVA, kunnen alleen geldige resultaten opleveren als sprake is van een normale verdeling. Als je data scheef verdeeld zijn, kan het voorkomen dat je resultaten niet valide zijn.

De aanname van een normale verdeling is vooral belangrijk bij steekproeven kleiner dan 30 observaties. Als je steekproef meer dan 30 observaties bevat, dan kun je volgens de centrale limietstelling (central limit theorem) aannemen dat aan de aanname van normaliteit wordt voldaan.

Wat is een normale verdeling?

Er zijn twee parameters die bepalen hoe de normale verdeling eruitziet: het gemiddelde en de standaarddeviatie.

• Binnen één standaarddeviatie ligt 68,2% van de observaties (34,1% + 34,1%), binnen twee standaarddeviaties 95,2% en binnen drie standaarddeviaties 99,6%.
• De centrummaten (gemiddelde, modus en mediaan) hebben bij een normale verdeling dezelfde waarde.
• De data zijn symmetrisch verdeeld, zonder skewness (zero skew).

 

Wat doe je als je data niet normaal verdeeld zijn?

Als je variabele niet normaal verdeeld is, kun je kijken of je de data kunt transformeren. Het kan namelijk zijn dat een variabele zelf niet normaal verdeeld is, maar het logaritme of het kwadraat wel.

Als ook dit niet het geval is, kun je niet-parametrische toetsen gebruiken, zoals de Wilcoxon- of Mann-Whitney-toets, in plaats van de t-toets.