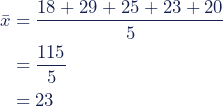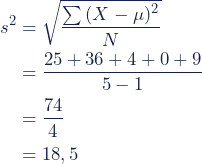Standaarddeviatie (Voorbeelden) | Berekenen, Interpreteren & Rapporteren

De standaarddeviatie of standaardafwijking geeft de mate van spreiding aan in bepaalde data. Het geeft aan hoezeer de geobserveerde waardes afwijken van het gemiddelde.

Stel dat je de leeftijden van vijf studenten hebt verzameld. De standaarddeviatie geeft dan een beeld van de leeftijdsverschillen tussen deze vijf studenten.

Een kleine standaarddeviatie duidt erop dat de studenten uit dezelfde (leeftijds)groep komen.

Standaardafwijking berekenen

Je kunt de standaardafwijking met de hand berekenen of met behulp van onze standaarddeviatie calculator hieronder.

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

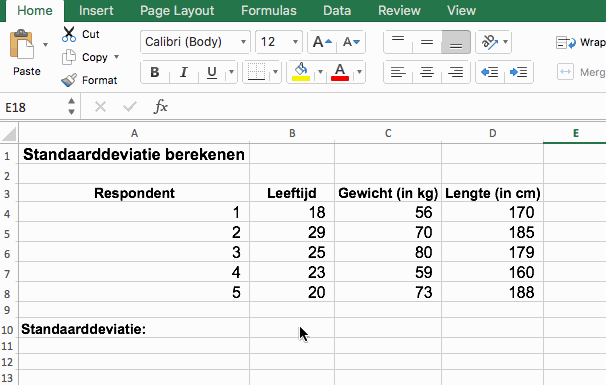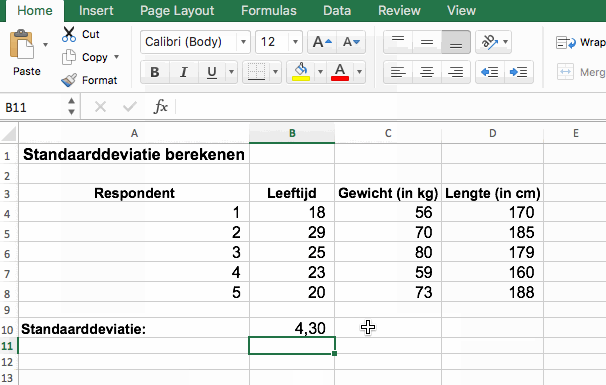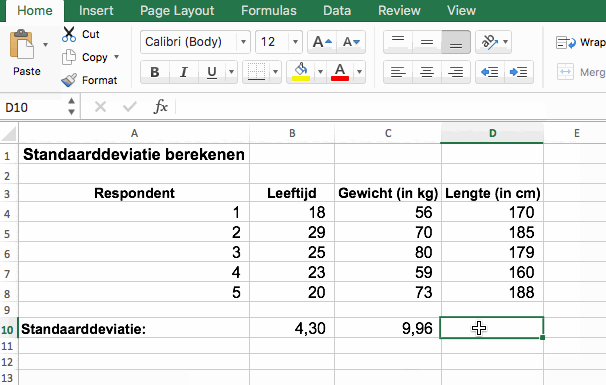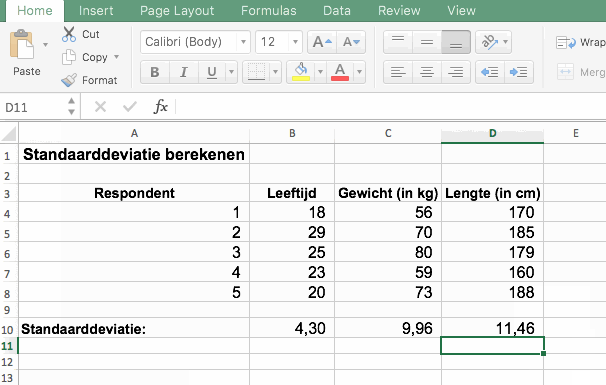
Standaarddeviatie berekenen met Excel of Google Sheets

Ga in een lege cel staan en vul de formule =STDEV.S() in. Tussen de haakjes selecteer je de gegevens waarna Excel de standaarddeviatie zal teruggeven. De .S achter STDEV laat Excel weten dat het hier om een steekproef gaat.

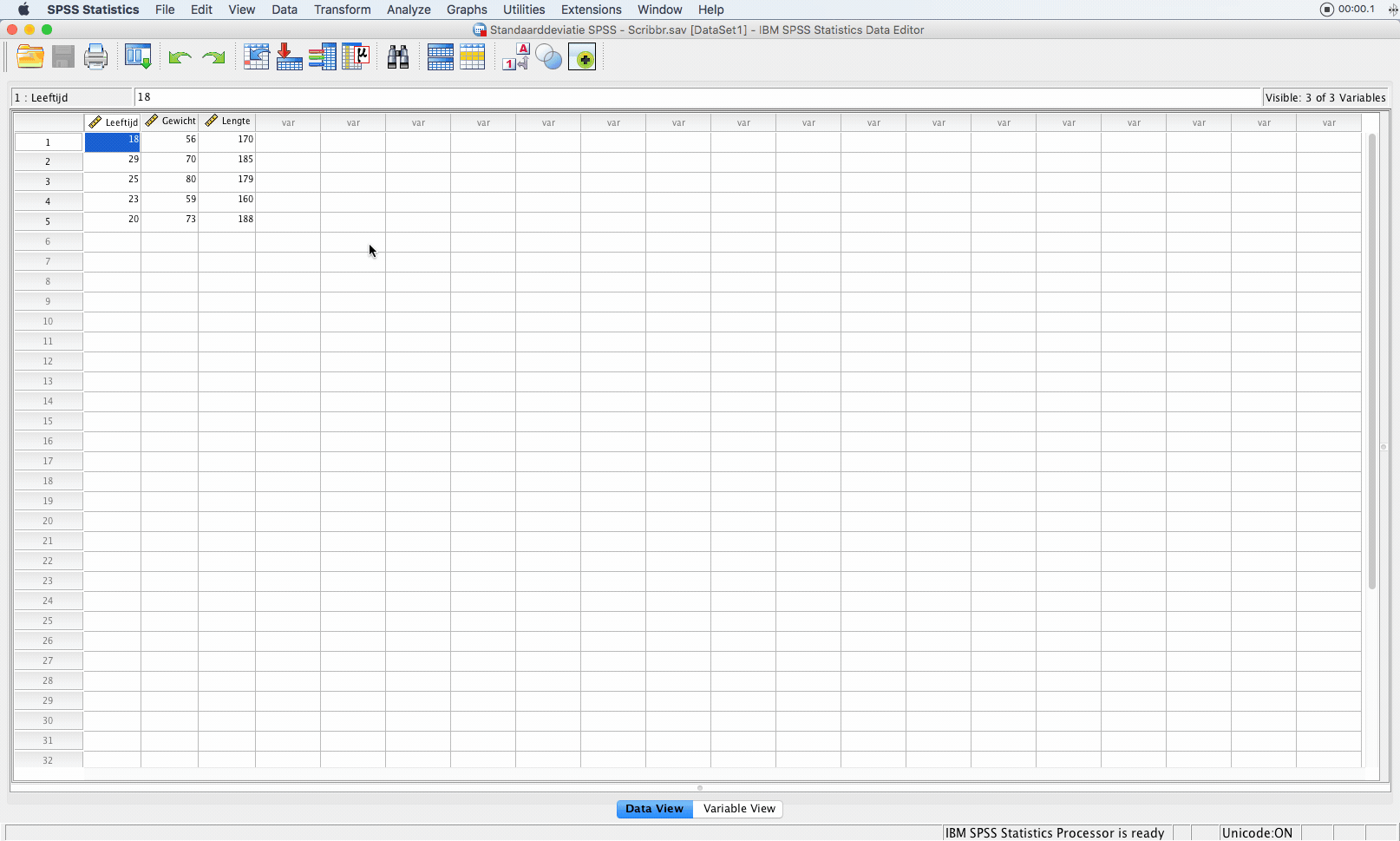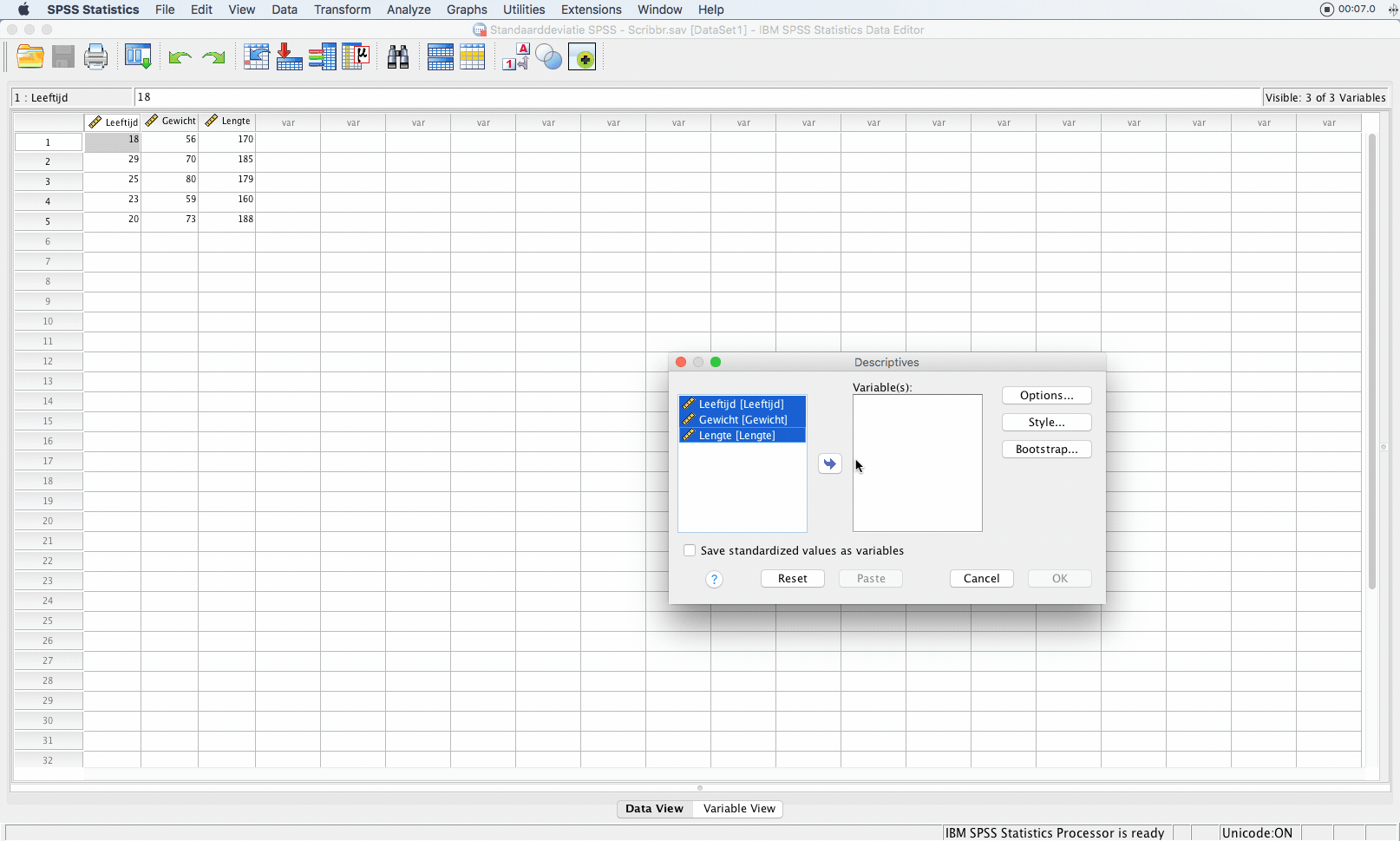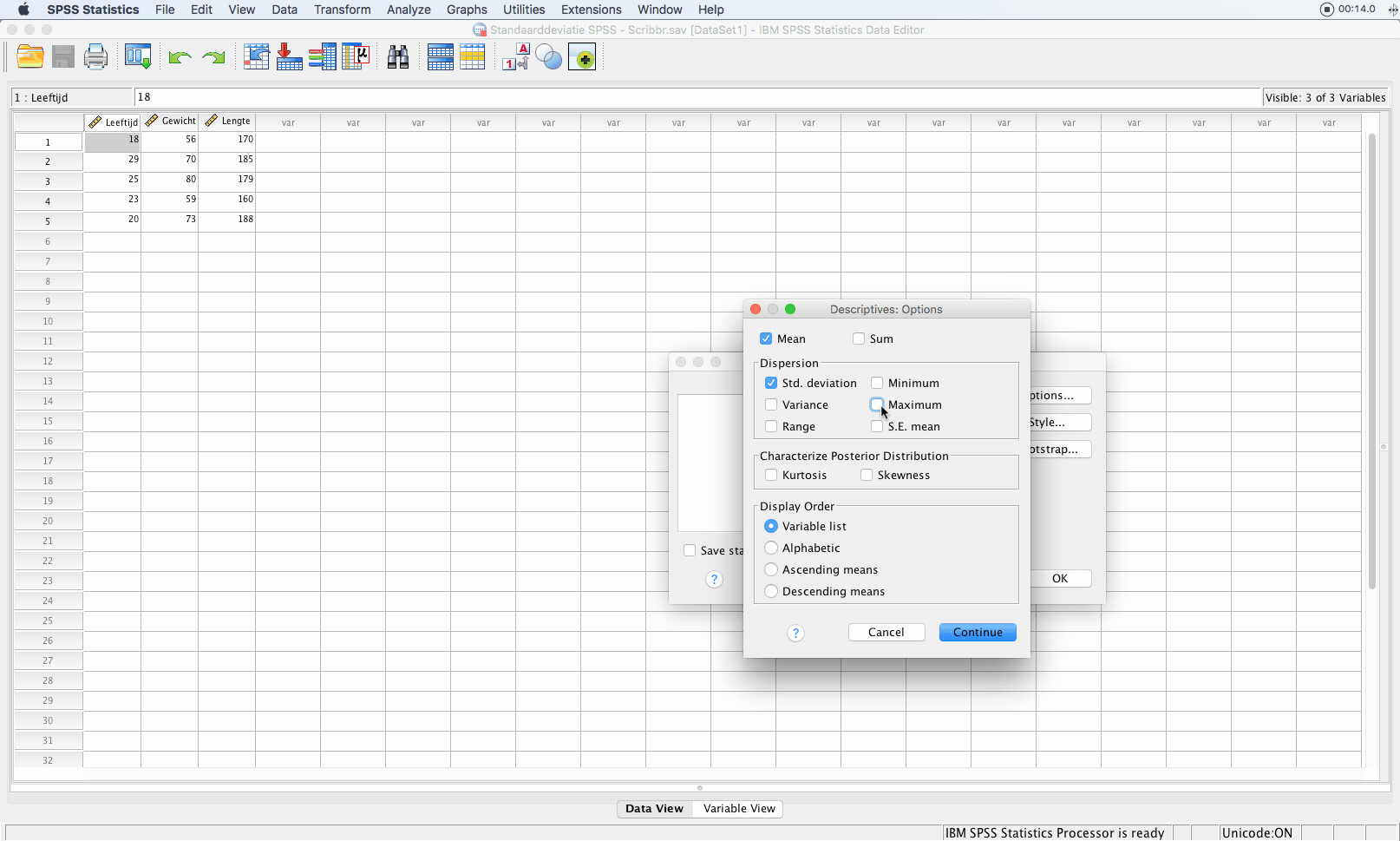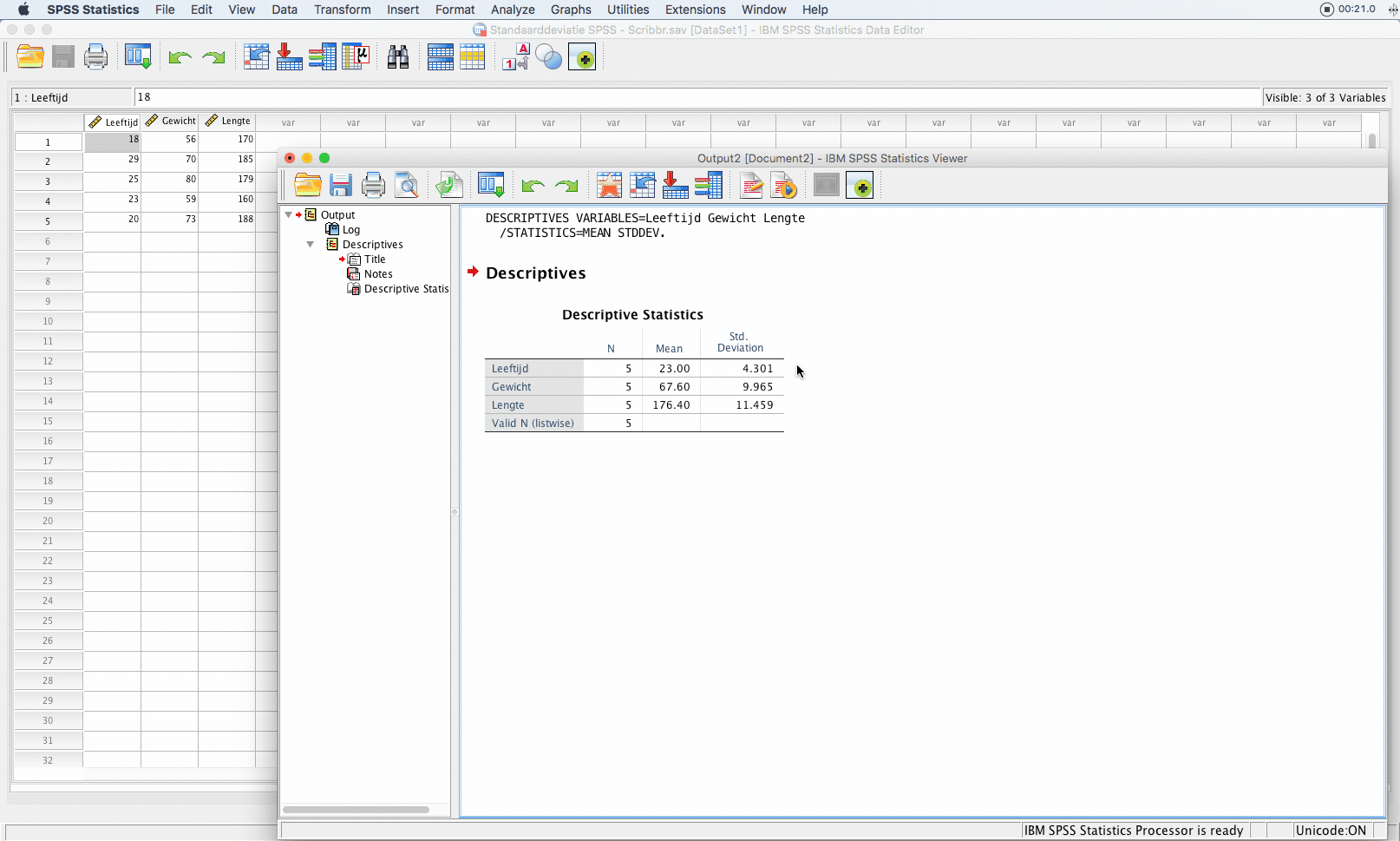
Standaarddeviatie berekenen met SPSS

Om de standaarddeviatie te bereken met SPSS klik je in de menubalk op:

• Analyze
• Descriptive Statistics
• Descriptives.

Er verschijnt een scherm waarin je variabelen (leeftijd, gewicht en lengte) selecteert die je wilt analyseren.

Klik vervolgens op ‘options…’ en kijk of ‘std. deviation’ is aangevinkt. Je kunt ook het gemiddelde (mean) aanvinken. Klik vervolgens op ‘continue’ en ‘ok’ om de analyse uit te voeren.

Wanneer gebruik je de standaarddeviatie?

In je methodologie beschrijf je vaak de kenmerken van je steekproef. Zo informeer je de lezer over wie aan je onderzoek heeft meegedaan. Je rapporteert de gemiddelde leeftijd, het geslacht en andere relevante kenmerken van de respondenten.

Een andere plek waar de standaarddeviatie vaak terugkomt is het resultatenhoofdstuk of bij het testen voor een normale verdeling van je data.

Standaarddeviatie rapporteren

De standaarddeviatie wordt in formules vaak aangeduid met de Griekse letter ‘σ’ (sigma). Echter, als je het hebt over de standaarddeviatie van een steekproef (in plaats van de hele populatie) gebruik je de letter ‘s’ in formules. In de lopende tekst kan je het beste de afkorting ‘SD’ gebruiken.

Voorbeeldzinnen die je kunt gebruiken zijn:

• De meeste geënquêteerde studenten zijn vrij jong (M = 23,3; SD = 4,30)
• De gemiddelde leeftijd van de studenten is 23,3 jaar (SD = 4,30)

Let op dat de afkortingen ‘M’ en ‘SD’ volgens de APA-stijl cursief gedrukt worden. Daarnaast gebruik je in het Nederlands komma’s voor een decimaal getal (23,3) en puntkomma’s om het gemiddelde en de standaardafwijking te scheiden. In het Engels gebruik je punten in een decimaal getal (23.00) en komma’s om te scheiden.

Meer informatie hierover vind je in ons artikel over de schrijfwijze van statistische resultaten volgens de APA-stijl.

Formule standaarddeviatie

Er bestaan twee formules om de standaarddeviatie te berekenen.

1. Standaarddeviatie van de hele populatie berekenen:
   
2. Standaarddeviatie van een steekproef berekenen:
   

De symbolen hebben de volgende betekenis:

= Som van alles dat tussen de haakjes volgt.
 = De observatie
= Populatiegemiddelde
= Steekproefgemiddelde
N = Populatiegrootte
n = Steekproefgrootte

Handmatig de standaarddeviatie berekenen

Om de standaarddeviatie handmatig te berekenen, doorloop je de volgende stappen:

1. Bereken het gemiddelde
2. Bereken de afwijking van iedere waarde tot het gemiddelde en kwadrateer deze
3. Deel deze gekwadrateerde afwijkingen door het aantal observaties minus één
4. Neem de wortel van de variantie om de standaarddeviatie te krijgen

Stel dat je vijf studenten hebt gevraagd naar hun leeftijd. Wat is dan de standaarddeviatie (ofwel spreiding) in deze waardes?

Stap 1: Gemiddelde berekenen

Tel de leeftijden bij elkaar op en deel dit door het aantal respondenten om het gemiddelde te berekenen:

Stap 2: Afwijking tot het gemiddelde berekenen en kwadrateren

Bereken de afwijking van het gemiddelde. Dus de leeftijden – gemiddelde .
Vervolgens kwadrateer je deze waarde (.

Stap 3: Delen door het aantal observaties minus één

Als je de gekwadrateerde afwijkingen optelt en deze vervolgens deelt door het aantal respondenten minus één krijg je de variantie.

Waarom -1? Omdat anders de standaarddeviatie onderschat wordt. Dit doe je altijd wanneer je data analyseert van een steekproef.

Stap 4: Wortel variantie trekken

Een variantie van 18,5 is lastig te interpreteren. Wat zegt dit nu precies over de spreiding rond het gemiddelde? Precies om deze reden willen we de standaarddeviatie weten. Om dit te berekenen neem je de wortel van de variantie, dus √ 18,5 = 4,30.

Ervan uitgaande dat de data normaal verdeeld is, betekent dit dat 68% van de respondenten (1 standaarddeviatie) tussen de 18,7 en 27,3 jaar oud is (gemiddelde +/- standaarddeviatie van 4,30).

Veelgestelde vragen

Wat is de standaarddeviatie?

De standaarddeviatie (standard deviation of s) is de gemiddelde hoeveelheid variabiliteit in je dataset. Deze maat vertelt je hoe ver iedere score gemiddeld van het gemiddelde verwijderd is. Des te groter de standaarddeviatie, des te meer variabel je dataset is.

Hoe bereken je de standaarddeviatie?

Er zijn zes stappen om de standaarddeviatie te berekenen (al kun je deze maat in Excel of SPSS automatisch laten berekenen).

1. Maak een lijst van alle scores en vind het gemiddelde.
2. Trek het gemiddelde af van iedere score om de afstand (afwijking) tot het gemiddelde te berekenen.
3. Bereken voor iedere afwijking het kwadraat.
4. Tel alle gekwadrateerde afwijkingen bij elkaar op.
5. Deel de som van de gekwadrateerde afwijkingen door N – 1.
6. Trek de wortel van het gevonden nummer bij stap 5.

Wat is het verschil tussen beschrijvende en toetsende statistiek?

Met beschrijvende statistiek (ook wel descriptieve statistiek genoemd) vat je de kenmerken van een dataset samen. Met toetsende statistiek (ook wel inferentiële of verklarende statistiek genoemd) toets je een hypothese of bepaal je of je data generaliseerbaar zijn naar een bredere populatie.

Wat zijn de drie belangrijkste beschrijvende statistieken?

De drie belangrijkste beschrijvende statistieken hebben betrekking op de frequentieverdeling, centrale tendens en variabiliteit van de dataset.

• Verdeling (distribution) verwijst naar de frequentie waarmee bepaalde antwoorden voorkomen.
• Centrummaten (measures of central tendency) geven je het gemiddelde voor iedere vraag.
• Spreidingsmaten (measures of variability) laten je de mate van spreiding in de dataset zien.

Wat is standaardafwijking?

Standaardafwijking is een ander woord (synoniem) voor standaarddeviatie. De woorden betekenen dus hetzelfde.

Standaardafwijking of standaarddeviatie geeft de mate van spreiding weer in bepaalde data.