Centrale Limietstelling (Central Limit Theorem) | Formule
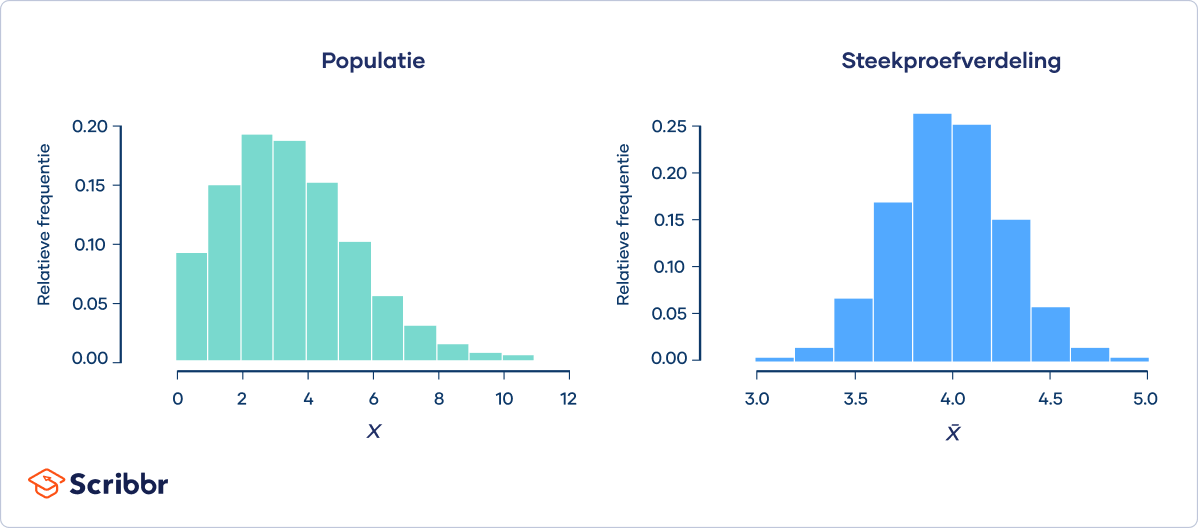
De centrale limietstelling (central limit theorem) stelt dat de gemiddelden van steekproeven altijd normaal verdeeld zullen zijn als je steekproeven van voldoende omvang neemt uit een populatie, zelfs als die populatie niet normaal verdeeld is.
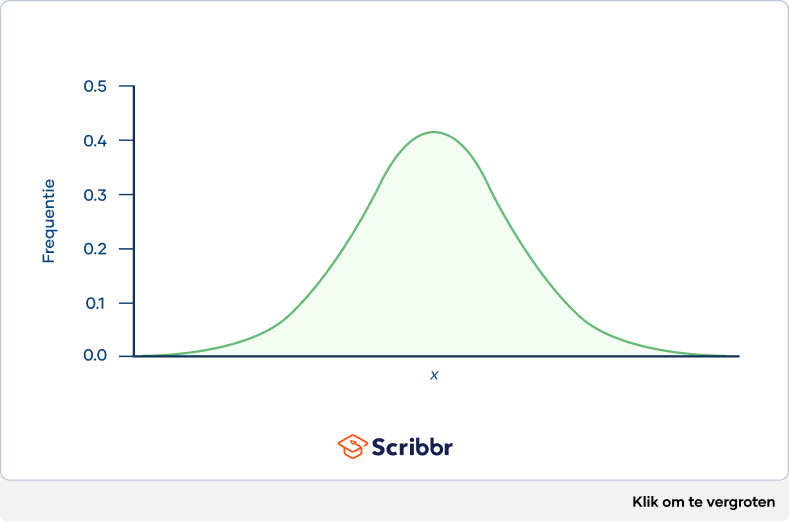
Op het rechterplaatje zie je dat de steekproefgemiddelden een normale verdeling volgen, zoals wordt voorspeld door de centrale limietstelling.
Inhoudsopgave
- Wat is de centrale limietstelling?
- Formule centrale limietstelling
- Steekproefgrootte en de centrale limietstelling
- Voorwaarden centrale limietstelling
- Belang van de centrale limietstelling
- Voorbeeld centrale limietstelling
- Oefenvragen
- Veelgestelde vragen over de centrale limietstelling (central limit theorem)
Wat is de centrale limietstelling?
De centrale limietstelling maakt gebruik van het concept steekproefverdeling. De steekproefverdeling is de kansverdeling van een statistiek voor een groot aantal steekproeven uit de populatie.
Om de steekproefverdeling beter te begrijpen, kan het helpen om een experiment voor te stellen:
- Stel dat je een aselecte steekproef trekt uit een populatie en een statistiek berekent voor deze steekproef, zoals het gemiddelde.
- Vervolgens trek je opnieuw een aselecte steekproef uit een populatie en bereken je hiervan weer het gemiddelde.
- Dit proces herhaal je heel vaak, waardoor je uiteindelijk een groot aantal steekproefgemiddelden krijgt. Elk gemiddelde hoort bij één steekproef.
De verdeling van de steekproefgemiddelden is een voorbeeld van een steekproefverdeling.
De centrale limietstelling zegt dat de steekproefverdeling van het gemiddelde altijd normaal verdeeld zal zijn, mits de steekproefgrootte groot genoeg is. Het maakt hiervoor niet uit of de verdeling van de populatie normaal, Poisson, binomiaal of anders verdeeld is.
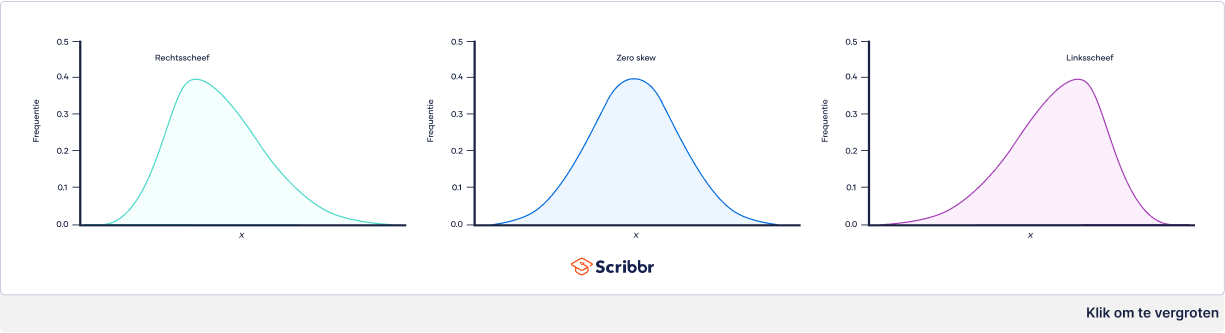
Een normale verdeling is een symmetrische, klokvormige verdeling met steeds minder waarnemingen naarmate de waarden verder van het middelpunt van de verdeling afliggen.
Lees waarom zo veel studenten Scribbr inschakelen
Formule centrale limietstelling
Gelukkig is het niet nodig om herhaaldelijk een steekproef uit de populatie te trekken om achter de vorm van de steekproefverdeling te komen. De parameters van de steekproefverdeling van het gemiddelde worden bepaald door de parameters van de populatie:
- Het gemiddelde van de steekproefverdeling is het gemiddelde van de populatie.
- De standaarddeviatie van de steekproefverdeling is de standaarddeviatie van de populatie, gedeeld door de vierkantswortel van de steekproefgrootte.
Je kunt de steekproefverdeling van het gemiddelde met deze notatie beschrijven:
Waarbij:
- X̄ = de steekproefverdeling van de steekproefgemiddelden
- ~ = een symbool dat staat voor “volgt de verdeling”
- N = de normale verdeling
- µ = het gemiddelde van de populatie
- σ = de standaardafwijking van de populatie
- n = de steekproefgrootte
Steekproefgrootte en de centrale limietstelling
De steekproefgrootte (n) is het aantal waarnemingen dat voor elke steekproef uit de populatie wordt getrokken. De steekproefgrootte is voor alle steekproeven gelijk.
De steekproefgrootte beïnvloedt de steekproefverdeling van het gemiddelde op twee manieren:
-
Steekproefgrootte en normaliteit
Hoe groter de steekproefgrootte, hoe beter de steekproefverdeling een normale verdeling zal volgen.
Als de steekproefgrootte klein is, is de steekproefverdeling van het gemiddelde soms niet-normaal verdeeld. Dat komt omdat de centrale limietstelling alleen opgaat als de steekproefgrootte “voldoende groot” is.
Over het algemeen wordt een steekproefgrootte van 30 als voldoende groot beschouwd.
- Als n < 30, is de centrale limietstelling niet van toepassing. De steekproefverdeling zal dan een soortgelijke verdeling volgen als die van de populatie. Daarom zal de steekproefverdeling dan alleen normaal verdeeld zijn als de populatie ook normaal verdeeld is.
- Als n > 30, is de centrale limietstelling wel van toepassing. De steekproefverdeling zal bij benadering een normale verdeling volgen.
-
Steekproefgrootte en standaarddeviaties
De steekproefgrootte beïnvloedt de standaarddeviatie van de steekproefverdeling. De standaarddeviatie of standaardafwijking is een maat voor de spreiding of variabiliteit van de verdeling (i.e., hoe breed of smal de verdeling is).
- Als n klein is, is de standaarddeviatie groot. Er is veel spreiding in de gemiddelden van de steekproeven omdat ze geen exacte schattingen zijn van het gemiddelde van de populatie.
- Als n groot is, is de standaarddeviatie klein. Er is niet veel spreiding in de gemiddelden van de steekproeven omdat ze precieze schattingen zijn van het gemiddelde van de populatie.
Voorwaarden centrale limietstelling
De centrale limietstelling stelt dat de steekproefverdeling van het gemiddelde altijd een normale verdeling zal volgen onder de volgende voorwaarden:
- De steekproefgrootte is voldoende groot. Aan deze voorwaarde wordt meestal voldaan als de steekproefgrootte n ≥ 30 is.
- De steekproeven zijn onafhankelijke en identiek verdeelde willekeurige variabelen (independent and identically distributed random variables, ook wel i.i.d. genoemd). Aan deze voorwaarde wordt meestal voldaan als de steekproeven aselect zijn getrokken.
- De verdeling van de populatie heeft een eindige variantie. De centrale limietstelling is niet van toepassing op verdelingen met een oneindige variantie, zoals de Cauchy-verdeling. De meeste verdelingen hebben een eindige variantie.
Belang van de centrale limietstelling
De centrale limietstelling is één van de meest belangrijke statistische stellingen. Dankzij de centrale limietstelling kunnen uitspraken worden gedaan over de vaak onbekende verdeling van de populatie, zelfs bij een niet-normale verdeling.
De centrale limietstelling stelt namelijk dat de steekproefverdeling van het gemiddelde altijd normaal verdeeld moet zijn, waardoor deze achterhaald kan worden én ons iets kan vertellen over de populatieparameters.
Voorbeeld centrale limietstelling
Om de centrale limietstelling beter te begrijpen, kan het helpen de stelling op echte verdelingen toe te passen.
Continue kansverdeling
Stel dat je geïnteresseerd bent in de leeftijd waarop mensen met pensioen gaan in Nederland.
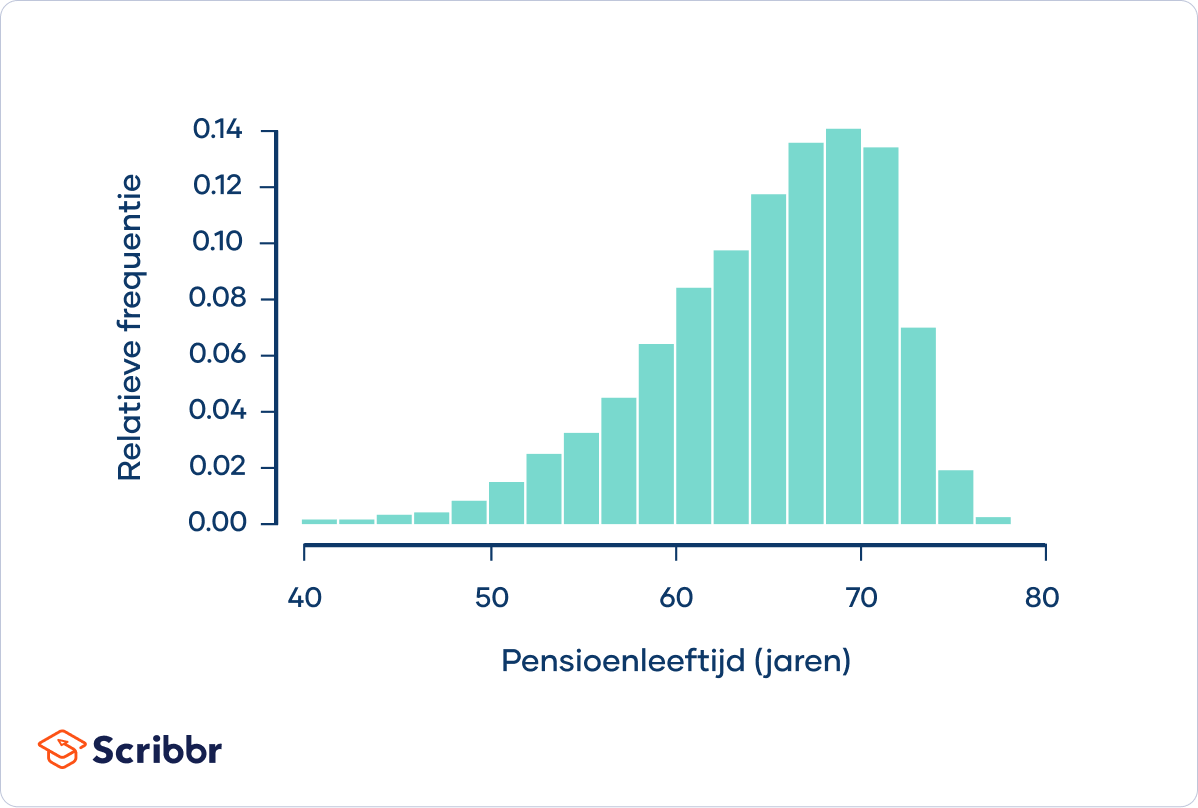
Je populatie bestaat uit gepensioneerde Nederlanders, en de verdeling van de populatie zou er ongeveer zo uit kunnen zien:
De pensioenleeftijd volgt een linksscheve verdeling. De meeste mensen gaan binnen ongeveer vijf jaar na de gemiddelde pensioenleeftijd van 65 jaar met pensioen. Er is echter een “lange staart” met minder voorkomende leeftijden van de mensen die veel jonger met pensioen gaan, bijvoorbeeld op hun 50e of zelfs op hun 40e. De populatie heeft een standaarddeviatie van 6 jaar.
Stel dat je een kleine steekproef uit de populatie neemt. Je selecteert willekeurig vijf gepensioneerden en vraagt hen op welke leeftijd zij met pensioen zijn gegaan.
| 68 | 73 | 70 | 62 | 63 |
Het gemiddelde van de steekproef is een schatting van het populatiegemiddelde, maar het is misschien geen hele nauwkeurige schatting, aangezien de steekproefgrootte slechts 5 is.
Gemiddelde = 67.2 jaar
Stel dat je deze procedure 10 keer herhaalt, waarbij je steekproeven neemt van 5 gepensioneerden, en het gemiddelde van elke steekproef berekent. Dit is een steekproefverdeling van het gemiddelde.
| 60.8 | 57.8 | 62.2 | 68.6 | 67.4 | 67.8 | 68.3 | 65.6 | 66.5 | 62.1 |
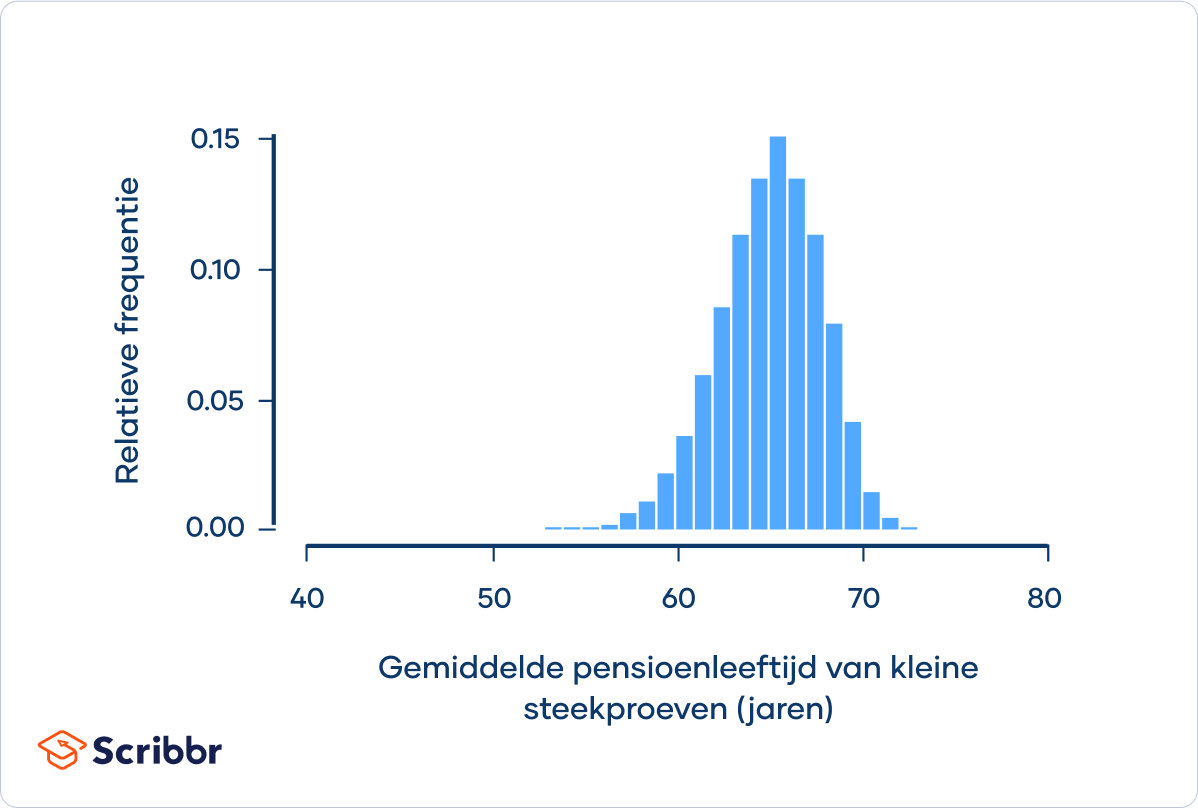
Als je deze procedure heel vaak herhaalt, zal de histogram van de steekproefgemiddelden er uiteindelijk ongeveer zo uit komen te zien:
Hoewel deze steekproefverdeling normaler verdeeld is dan de populatie, is de verdeling nog steeds een beetje linksscheef.
Merk ook op dat de spreiding van de steekproefverdeling kleiner is dan de spreiding van de populatie.
De centrale limietstelling stelt dat de steekproefverdeling van het gemiddelde altijd een normale verdeling zal volgen als de steekproefgrootte voldoende groot is. Deze steekproefverdeling is niet normaal verdeeld omdat de steekproefgrootte niet voldoende groot is.
Stel je nu voor dat je een grote steekproef uit de populatie neemt. Je selecteert willekeurig 50 gepensioneerden en vraagt ze op welke leeftijd ze met pensioen zijn gegaan.
| 73 | 49 | 68 | 72 | 71 | 65 | 60 | 69 | 61 | 62 |
| 75 | 66 | 63 | 66 | 68 | 76 | 68 | 54 | 74 | 68 |
| 60 | 72 | 63 | 57 | 64 | 65 | 59 | 72 | 52 | 52 |
| 72 | 69 | 62 | 68 | 64 | 60 | 65 | 53 | 69 | 59 |
| 68 | 67 | 71 | 69 | 70 | 52 | 62 | 64 | 68 |
Het gemiddelde van de steekproef is een schatting van het populatiegemiddelde. Het is een nauwkeurige schatting, omdat de steekproef voldoende groot is.
Je kunt deze procedure weer vaak herhalen door meer steekproeven van de populatie te nemen en het gemiddelde van elke steekproef te berekenen.
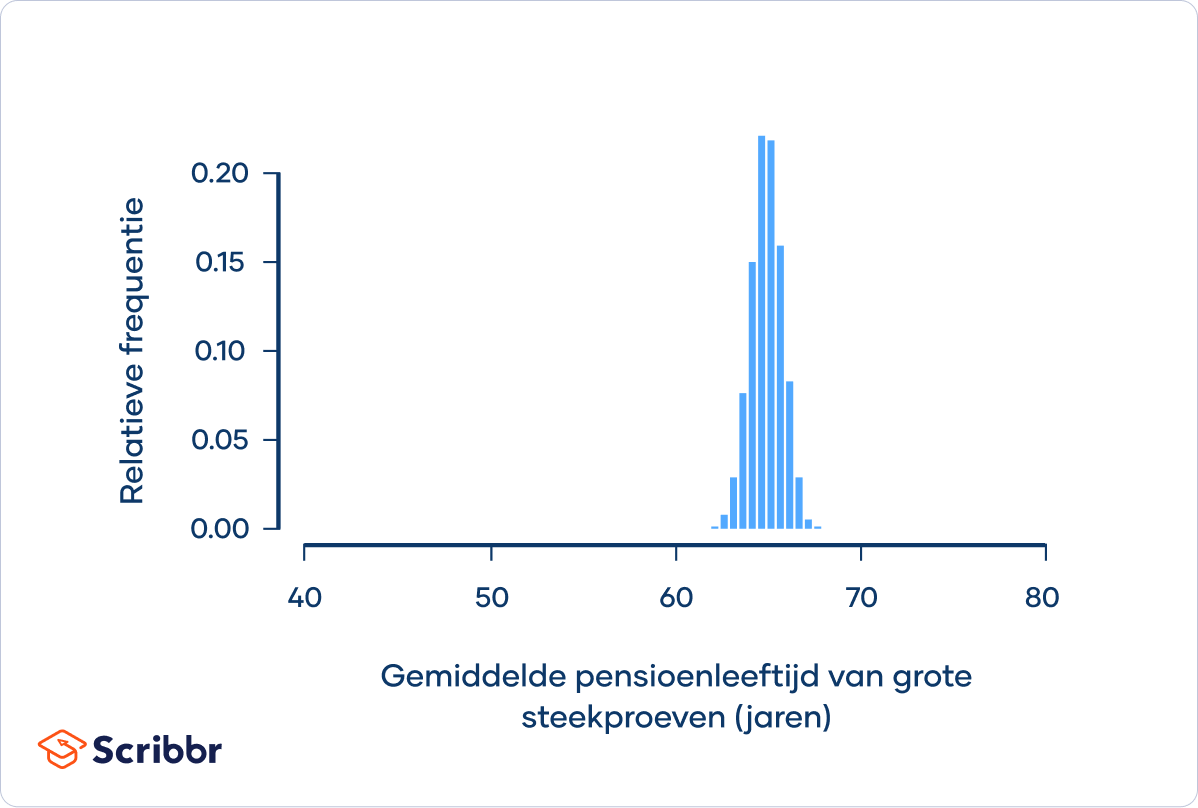
In het histogram kun je zien dat de steekproefverdeling normaal verdeeld is, zoals wordt voorspeld door de centrale limietstelling.
De standaarddeviatie van deze steekproefverdeling is 0.85 jaar, wat minder is dan de spreiding van de kleine steekproefverdeling, en veel minder dan de spreiding van de populatie. Als je de steekproefgrootte verder zou vergroten, zou de spreiding nog kleiner worden.
Je kunt de formule van de centrale limietstelling gebruiken om de steekproefverdeling te beschrijven:
µ = 65
σ = 6
n = 50
Discrete kansverdeling
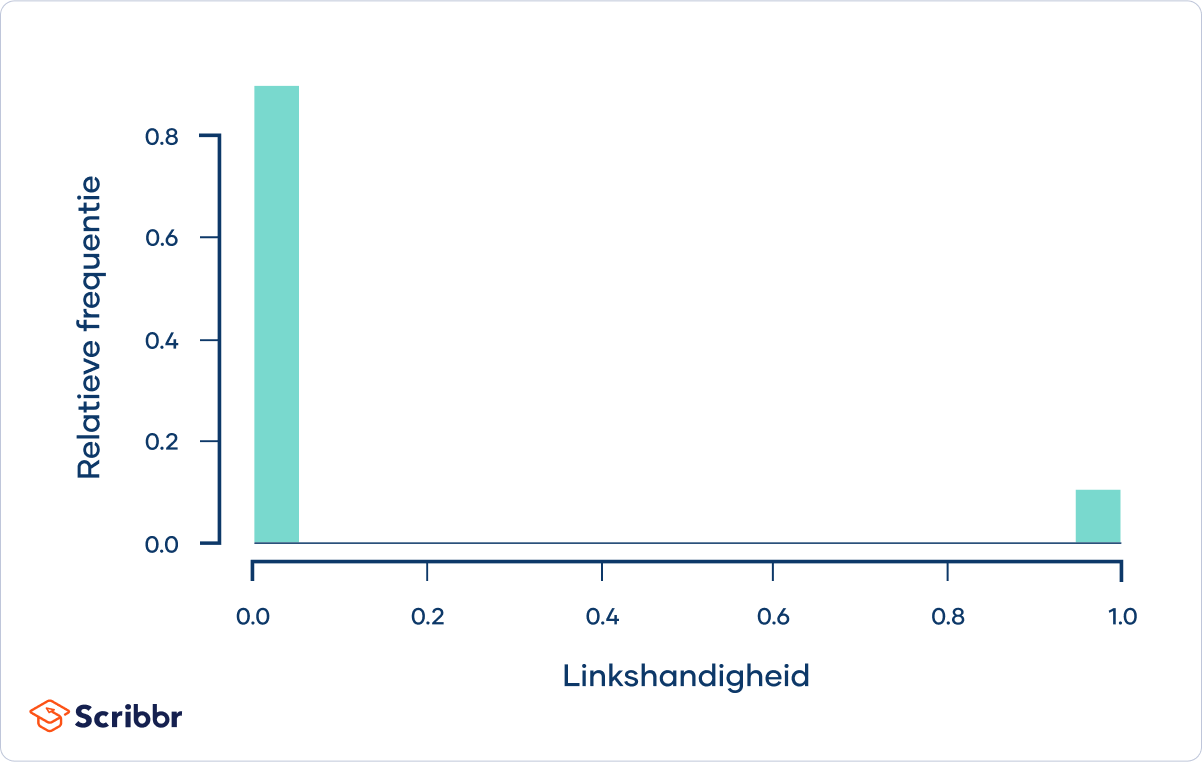
Ongeveer 10% van de mensen is linkshandig. Als we een waarde van 1 toekennen aan linkshandigheid en een waarde van 0 aan rechtshandigheid, dan ziet de kansverdeling van linkshandigheid voor de populatie van alle mensen eruit als volgt:
Het populatiegemiddelde is het percentage linkshandigen (0.1). De standaarddeviatie van de populatie is 0.3.
Stel dat je een willekeurige steekproef van vijf mensen neemt en hen vraagt of ze linkshandig zijn.
| 0 | 0 | 0 | 1 | 0 |
Het gemiddelde van de steekproef is een schatting van het populatiegemiddelde, maar het is misschien geen hele nauwkeurige schatting, aangezien de steekproefgrootte 5 is.
Gemiddelde = 0.2
Stel dat je deze procedure 10 keer herhaalt, waarbij je steekproeven neemt van vijf mensen, en het gemiddelde van elke steekproef berekent. Dit is een steekproefverdeling van het gemiddelde.
| 0 | 0 | 0.4 | 0.2 | 0.2 | 0 | 0.4 | 0 |
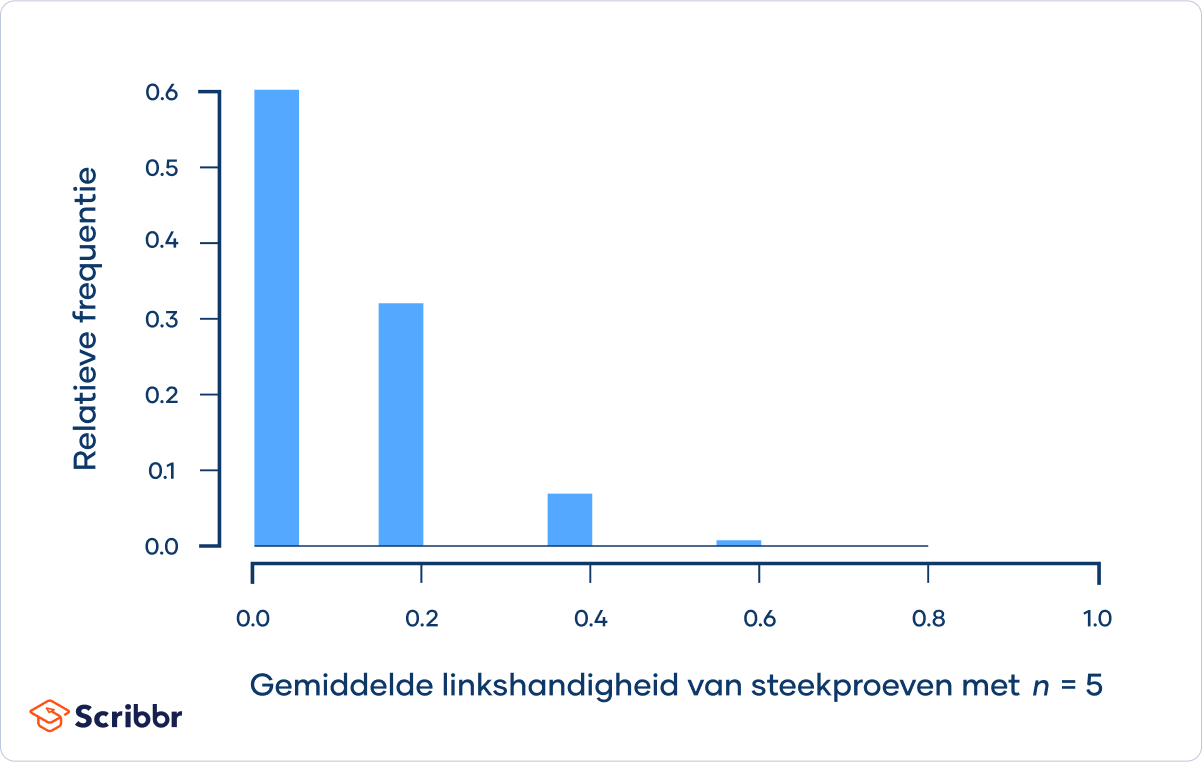
Als je deze procedure heel vaak herhaalt, zal het histogram van de steekproefgemiddelden er uiteindelijk ongeveer zo uit komen te zien:
De steekproefverdeling is niet normaal verdeeld, omdat de steekproefgrootte niet voldoende groot is om te voldoen aan de voorwaarden voor de centrale limietstelling.
Naarmate de steekproefgrootte toeneemt, gaat de steekproefverdeling steeds meer op een normale verdeling lijken, en neemt de spreiding af:
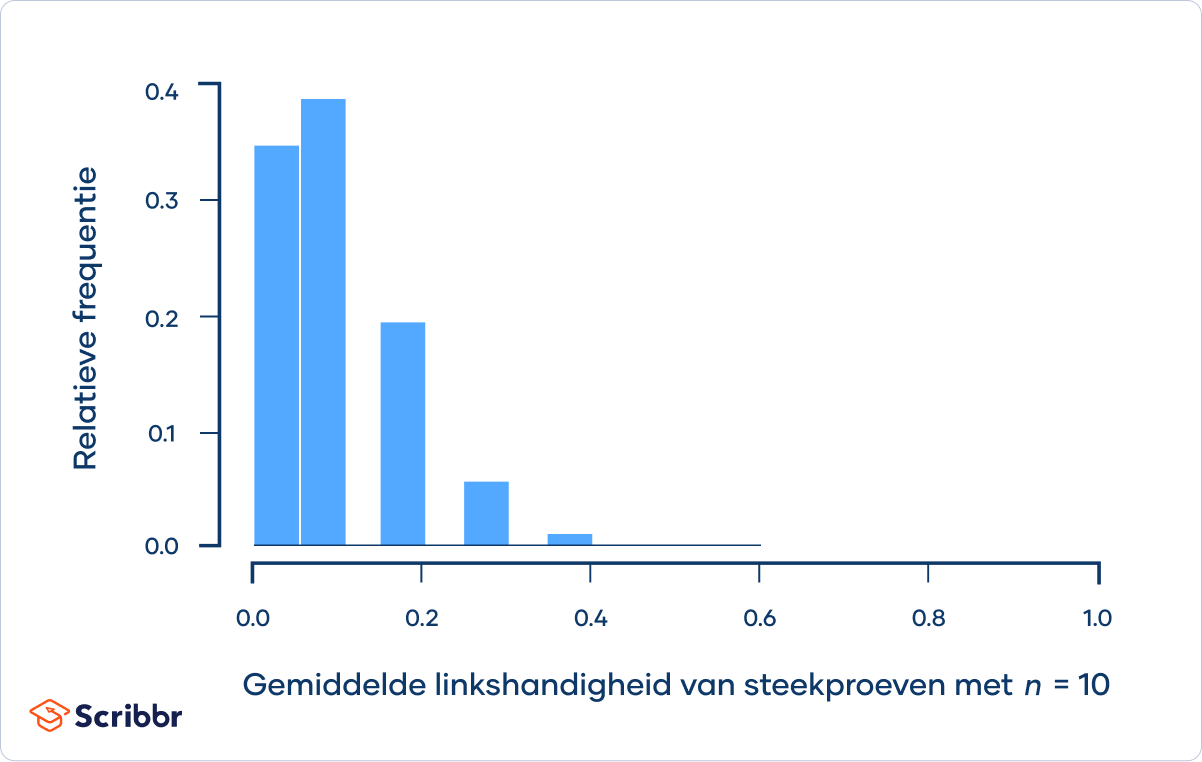
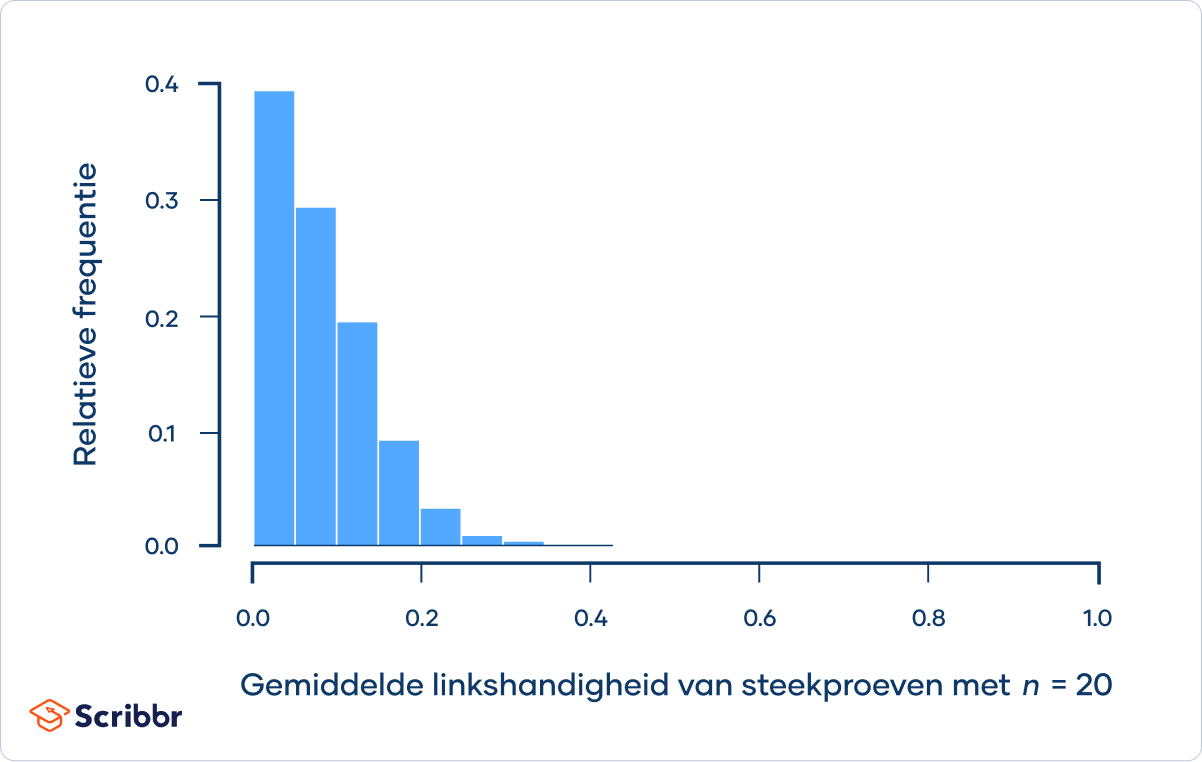
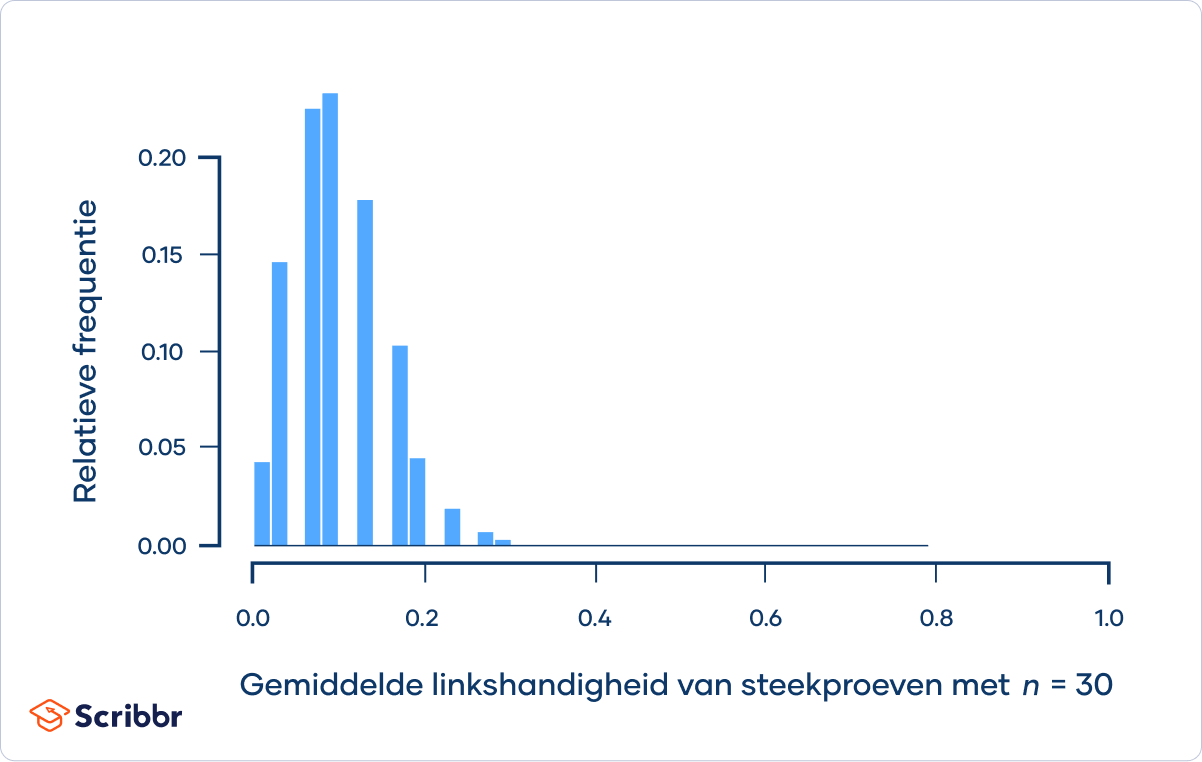
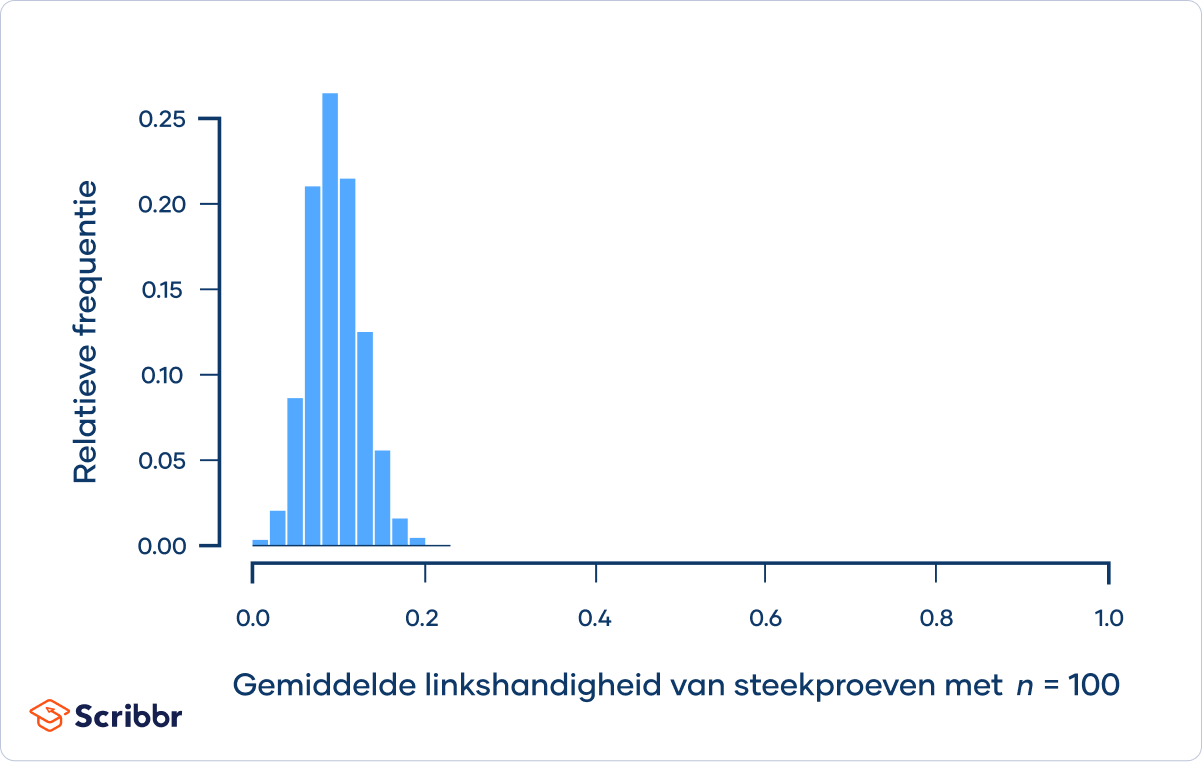
De steekproefverdeling van het gemiddelde voor steekproeven met n = 30 benadert de normale verdeling. Als de steekproef verder wordt uitgebreid tot n = 100, zie je dat de steekproefverdeling een normale verdeling volgt.
Je kunt de formule van de centrale limietstelling gebruiken om de steekproefverdeling voor n = 100 te beschrijven:
µ = 0.1
σ = 0.3
n = 100
Oefenvragen
Veelgestelde vragen over de centrale limietstelling (central limit theorem)
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Scharwächter, V. (2022, 16 augustus). Centrale Limietstelling (Central Limit Theorem) | Formule. Scribbr. Geraadpleegd op 2 juli 2025, van https://www.scribbr.nl/statistiek/centrale-limietstelling/