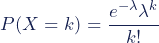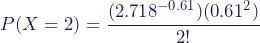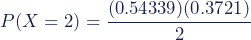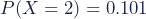Poissonverdeling (Poisson Distribution) | Formule & Voorbeelden
Een Poissonverdeling (Poisson distribution) is een discrete kansverdeling. De verdeling weergeeft de kans dat een gebeurtenis zich een bepaald aantal keren (k) binnen een bepaald tijds- of ruimte-interval voordoet.
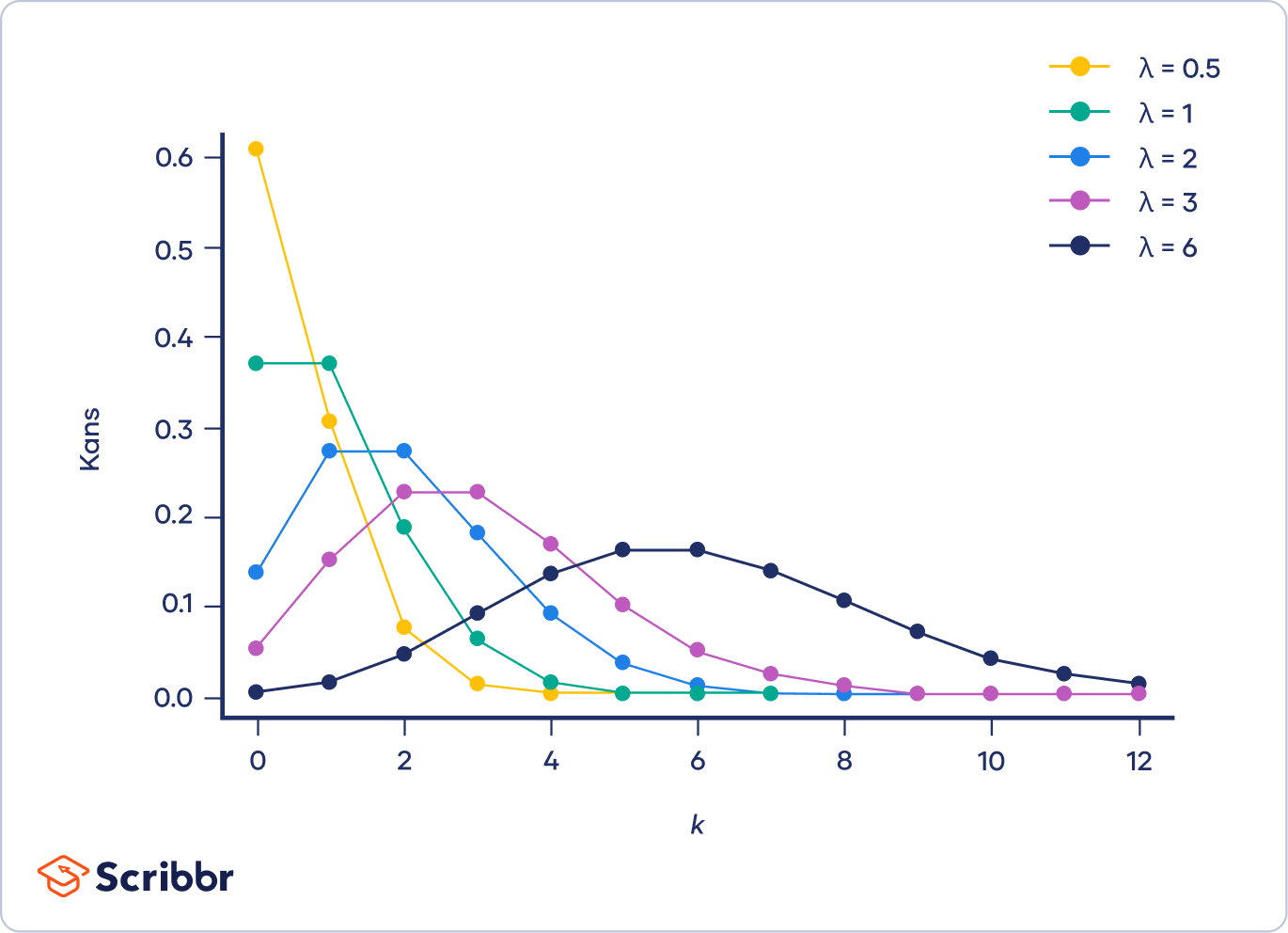
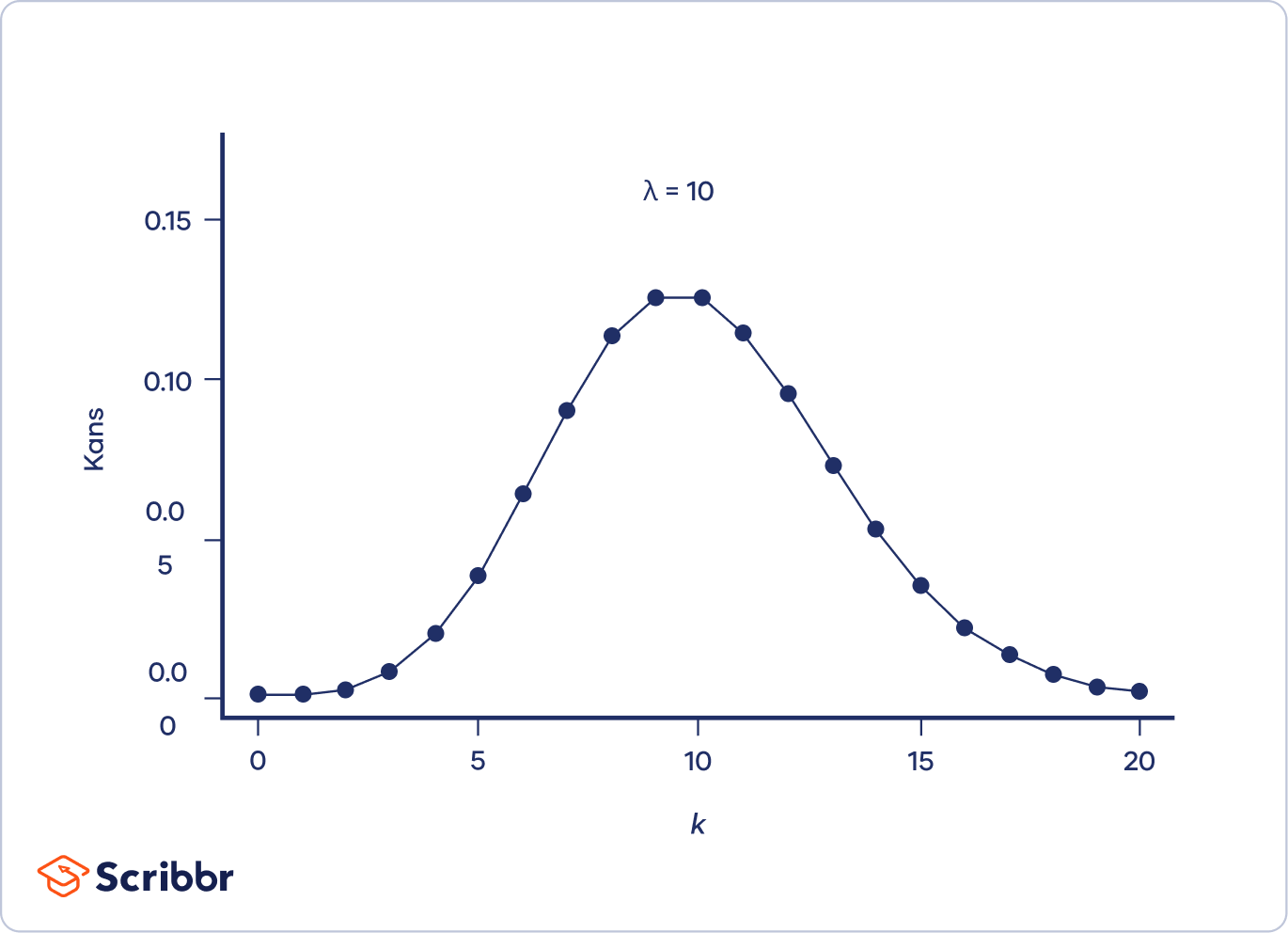
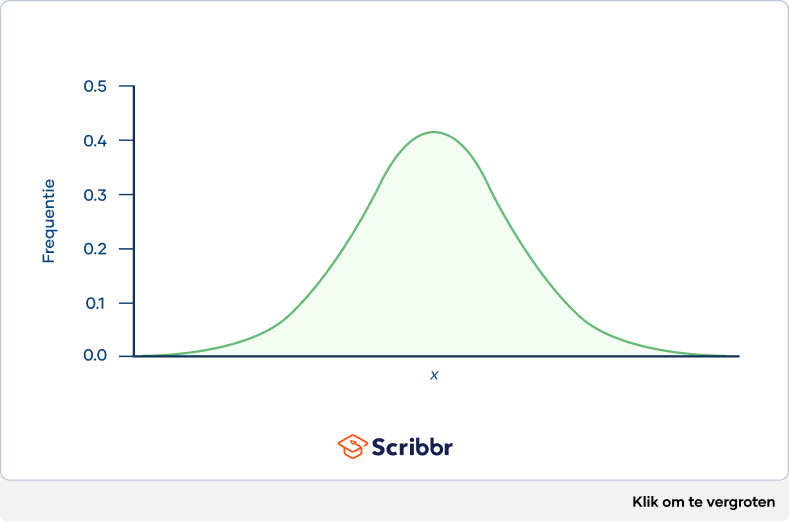
De Poissonverdeling heeft slechts één parameter, λ (lambda), die het gemiddelde aantal gebeurtenissen representeert. De onderstaande grafiek toont voorbeelden van Poissonverdelingen met verschillende waarden van λ.
Wat is een Poissonverdeling?
Een Poissonverdeling is een discrete kansverdeling, wat betekent dat deze de kans geeft op een discrete (i.e., telbare) uitkomst. Voor Poissonverdelingen is de discrete uitkomst het aantal keren dat een gebeurtenis zich voordoet, weergegeven door k.
Je kunt een Poissonverdeling gebruiken om het aantal gebeurtenissen te voorspellen of te verklaren dat binnen een bepaald tijds- of ruimte-interval optreedt. “Gebeurtenissen” (events) kunnen van alles zijn: van ziektegevallen tot klantenaankopen tot meteoorinslagen. Het interval kan een specifieke tijd of ruimte zijn, zoals 10 dagen of 5 vierkante centimeter.
Je kunt een Poissonverdeling gebruiken als:
- Individuele gebeurtenissen willekeurig en onafhankelijk van elkaar gebeuren. Dit betekent dat de waarschijnlijkheid van één gebeurtenis geen invloed heeft op de waarschijnlijkheid van een andere gebeurtenis.
- Je het gemiddelde aantal gebeurtenissen kent dat zich binnen een bepaald tijds- of ruimte-interval voordoet. Dit getal heet λ (lambda) en wordt verondersteld constant te zijn.
Als gebeurtenissen een Poissonverdeling volgen, is λ het enige dat je moet weten om de kans te berekenen dat een gebeurtenis een bepaald aantal keren optreedt.
Voorbeelden van Poissonverdelingen
In het algemeen zijn Poissonverdelingen vaak geschikt voor teldata. Teldata zijn samengesteld uit waarnemingen die niet-negatieve, gehele getallen zijn (i.e., getallen die worden gebruikt om te tellen, zoals 0, 1, 2, 3, 4, enzovoorts).
Sterfgevallen door paardenschoppen
Eén van de eerste toepassingen van de Poissonverdeling was van statisticus Ladislaus Bortkiewicz. Eind 1800 onderzocht hij de toevallige sterfgevallen door de schop van een paard van soldaten in het Pruisische leger. Hij analyseerde 20 jaar aan data voor 10 legerkorpsen, wat overeenkomt met 200 jaar waarnemingen van één korps.
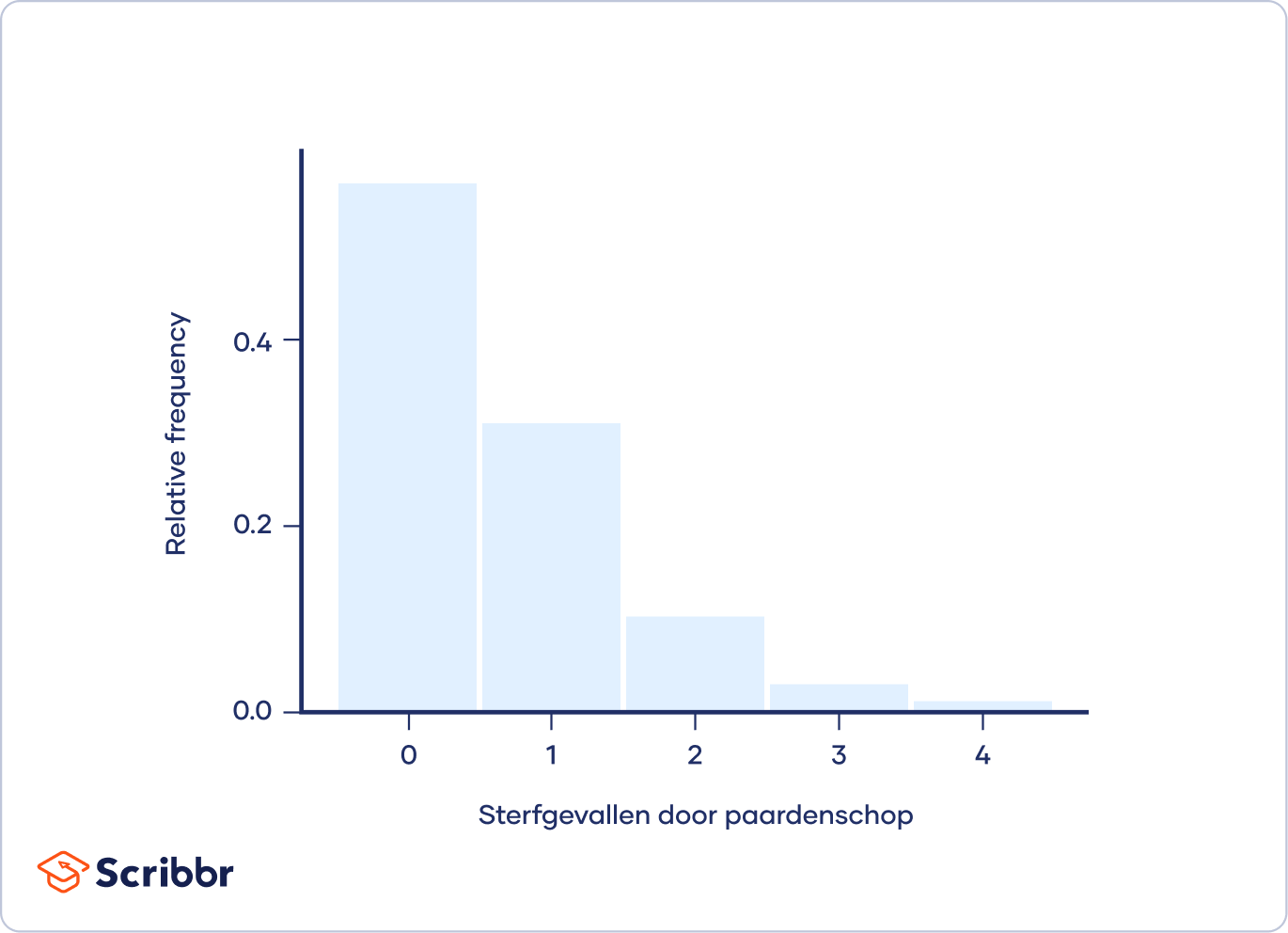
Het onderstaande histogram toont gesimuleerde data die lijken op wat Bortkiewicz heeft waargenomen:
Hij stelde vast dat gemiddeld 0.61 soldaten per korps per jaar stierven door schoppen van paarden. De meeste jaren stierven er echter geen soldaten door paardentrappen. Aan de andere kant van het spectrum waren er in een tragisch jaar vier soldaten in hetzelfde korps die stierven door paardenschoppen.
In moderne terminologie:
- Een sterfgeval door een paardenschop is een “gebeurtenis” (event).
- Het tijdsinterval is een jaar.
- Het gemiddelde aantal gebeurtenissen per tijdsinterval, λ, is 0.61.
- Het aantal sterfgevallen door paardenschoppen in een bepaald jaar is k.
De legerkorpsen die Bortkiewicz observeerde waren een steekproef uit de populatie van alle Pruisische legerkorpsen. Door de willekeurige steekproefmethode volgen steekproeven zelden perfect een kansverdeling. Het aantal sterfgevallen door paardenschoppen in de steekproef volgt bij benadering een Poissonverdeling, waardoor we redelijkerwijs kunnen afleiden dat de populatie een Poissonverdeling volgt.
Andere voorbeelden van Poissonverdelingen
Sinds de tijd van Bortkiewicz zijn Poissonverdelingen gebruikt om vele andere dingen te beschrijven. Een Poissonverdeling kan bijvoorbeeld worden gebruikt om de volgende onderwerpen te verklaren of te voorspellen:
- Whatsapp-berichten per uur
- Mannelijke grizzlyberen per hectare
- Machinestoringen per jaar
- Websitebezoekers per maand
- Griepgevallen per jaar
Grafieken kansdichtheidsfuncties
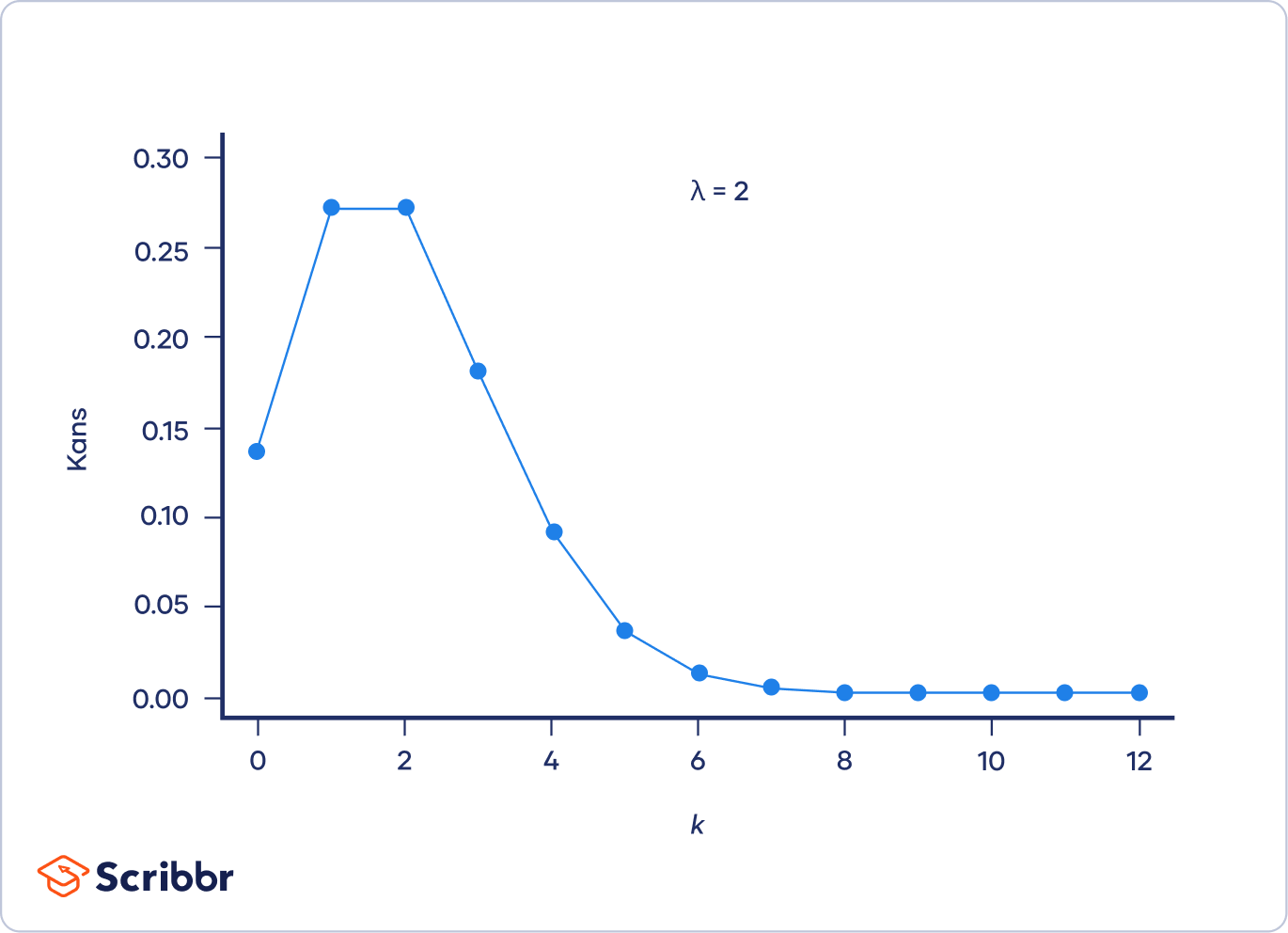
Een Poissonverdeling kan visueel worden voorgesteld als een grafiek van de kansdichtheidsfunctie (kansmassafunctie). Een kansdichtheidsfunctie is een functie die een discrete kansverdeling beschrijft.
Het meest waarschijnlijke aantal gebeurtenissen wordt voorgesteld door de piek van de verdeling – de modus.
- Als λ een niet-geheel getal is, is de modus het dichtstbijzijnde gehele getal dat kleiner is dan λ.
- Als λ een geheel getal is, zijn er twee modussen: λ en λ-1.
Als λ laag is, is de verdeling rechts van de piek veel langer dan links (i.e., de verdeling is rechtsscheef).
Naarmate λ toeneemt, lijkt de verdeling meer en meer op een normale verdeling. Als λ 10 of meer is, is een normale verdeling een goede benadering van de Poissonverdeling.
Gemiddelde en variantie van een Poissonverdeling
De Poissonverdeling heeft slechts één parameter, genaamd λ.
- Het gemiddelde van een Poissonverdeling is λ.
- De variantie van een Poissonverdeling is ook λ.
In de meeste verdelingen wordt het gemiddelde weergeven door µ (mu) en de variantie door σ² (sigma kwadraat). Omdat deze twee parameters bij een Poissonverdeling gelijk zijn, wordt hier het λ-symbool gebruikt om beide weer te geven.
Formule Poissonverdeling
De kansdichtheidsfunctie van de Poissonverdeling is:
Waarbij:
= een willekeurige variabele met een Poissonverdeling
= het aantal keren dat een gebeurtenis zich voordoet
) = de kans dat een gebeurtenis zich k keer voordoet
= de constante van Euler (ongeveer 2.718)
= het gemiddelde aantal keren dat een gebeurtenis optreedt
- ! = de factoriële functie
Berekening

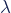

De kans dat er in 1898 precies twee soldaten in het VIIe legerkorps zijn omgekomen is 0.101.
Oefenvragen
Veelgestelde vragen over Poissonverdeling (Poisson distribution)
- Wat betekent “e” in de formule van de Poissonverdeling?
-
De e in de formule van de Poissonverdeling staat voor het getal 2.718. Dit getal wordt de constante van Euler genoemd. Je kunt e simpelweg vervangen door 2.718 als je een kans van de Poissonverdeling berekent. De constante van Euler is een heel nuttig getal en is vooral belangrijk in de wiskunde.
- Wat betekent lambda (λ) in de formule van de Poissonverdeling?
-
In de formule van de Poissonverdeling is lambda (λ) het gemiddelde aantal gebeurtenissen binnen een bepaald tijds- of ruimte-interval. Bijvoorbeeld: λ = 0.748 overstromingen per jaar.
- Wat is het verschil tussen een normale verdeling en een Poissonverdeling?
-
Deze tabel geeft een overzicht van de belangrijkste verschillen tussen een normale verdeling en een Poissonverdeling:
Kenmerk Normaal Poisson Continu of discreet Continu Discreet Parameter Gemiddelde (µ) en standaarddeviatie (σ) Lambda (λ) Vorm Klokvorm Afhankelijk van λ Symmetrie Symmetrisch Asymmetrisch (rechtsscheef). Naarmate λ toeneemt, neemt de asymmetrie af. Bereik −∞ tot ∞ 0 tot ∞ Als het gemiddelde van een Poissonverdeling groot is (> 10), kan deze worden benaderd door een normale verdeling. tromingen per jaar.
- Wat is een normale verdeling?
-
Er zijn twee parameters die bepalen hoe de normale verdeling eruitziet: het gemiddelde en de standaarddeviatie.
- Binnen één standaarddeviatie ligt 68,2% van de observaties (34,1% + 34,1%), binnen twee standaarddeviaties 95,2% en binnen drie standaarddeviaties 99,6%.
- De centrummaten (gemiddelde, modus en mediaan) hebben bij een normale verdeling dezelfde waarde.
- De data zijn symmetrisch verdeeld, zonder skewness (zero skew).
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Scharwächter, V. (2022, 24 augustus). Poissonverdeling (Poisson Distribution) | Formule & Voorbeelden. Scribbr. Geraadpleegd op 9 december 2024, van https://www.scribbr.nl/statistiek/poisson-verdeling/