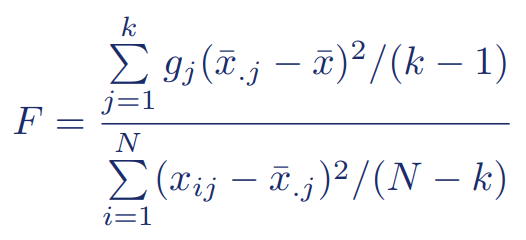ANOVA Uitvoeren en Interpreteren (Stappenplan met GIF's)

ANOVA staat voor Analysis of Variance, oftewel variantieanalyse, en wordt gebruikt om gemiddelden van meer dan twee groepen met elkaar te vergelijken. Het is een uitbreiding van de t-toets, die het gemiddelde van maximaal twee groepen met elkaar vergelijkt.

Voorbeeld: Je wilt weten of er een verschil in lengte bestaat tussen voetballers, turners, en volleyballers. Je vraagt aan al deze sporters hun lengte en gebruikt vervolgens een ANOVA om te kijken of de gemiddelde lengte van de groepen sporters verschilt.

Soorten ANOVA

Er bestaan verschillende soorten ANOVA. Welke je gebruikt hangt af van je data en je conceptueel model. One-way-ANOVA en two-way-ANOVA worden het meest gebruikt.

One-way-ANOVA

Je gebruikt een one-way-ANOVA als één groepsvariabele de groepen bepaalt en er maar één afhankelijke variabele is.

Voorbeeld: Je vergelijkt de gemiddelde lengte van verschillende typen sporters, zoals voetballers, turners en volleyballers. Het type sport dat iemand beoefent, is in dit geval de enige groepsvariabele en lengte is de enige afhankelijke variabele.

Two-way-ANOVA

Gebruik een two-way-ANOVA (ook wel factorial ANOVA) als je twee of meer groepsvariabelen in je conceptueel model hebt.

Voorbeeld: Je vergelijkt de gemiddelde lengte van verschillende typen sporters én hun geslacht. Er wordt dan niet alleen getest of het gemiddelde verschilt voor volleyballers en turners en voetballers, maar ook voor mannen en vrouwen, én voor mannelijke volleyballers en vrouwelijke volleyballers.

Multivariate ANOVA (MANOVA)

Gebruik een multivariate ANOVA (ook wel MANOVA) als je meerdere afhankelijke variabelen gebruikt. Je kunt deze ANOVA zowel gebruiken met een als meerdere groepsvariabelen.

Voorbeeld: Je wilt niet alleen niet alleen de gemiddelde lengte, maar ook het gemiddelde gewicht van verschillende groepen sporters vergelijken.

Je zou eventueel meerdere losse ANOVA’s kunnen uitvoeren. Dan wordt echter de kans op een type I fout (onterecht aannemen dat er wel verschillen tussen groepen bestaan) groter. Gebruik dus altijd de MANOVA als je meerdere afhankelijke variabelen hebt.

Repeated measures ANOVA

Je gebruikt een repeated measures ANOVA als je dezelfde groep respondenten meerdere malen onderzoekt (within-subjects design).

Voorbeeld: Je meet de gemiddelde lengte van respondenten in 2008, 2013, en 2018. Je vergelijkt dan de gemiddelde lengte van dezelfde persoon over een bepaalde periode om te kijken of deze verandert.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Voorwaarden ANOVA

Bij het uitvoeren van een ANOVA is het belangrijk om te controleren of aan een aantal voorwaarden is voldaan. Als er niet aan deze voorwaarden voldaan wordt dan kan het zijn dat je ten onrechte bepaalde conclusies trekt. De voorwaarden voor ANOVA zijn:

• De afhankelijke variabele wordt gemeten op ratio- of intervalniveau.
• De data per groep zijn verkregen uit een aselecte en willekeurige steekproef.
• De varianties voor elke groep zijn gelijk (homoscedasticiteit). Dit is te controleren met de ‘homogeneity of variance-test’ welke later wordt toegelicht.
• Binnen iedere groep bestaat een normale verdeling.

ANOVA uitvoeren met SPSS

Om de variantieanalyse (ANOVA) uit te voeren kun je het programma SPSS gebruiken. Lees of bekijk de GIF voor de stappen die je moet volgen. Download het SPSS-bestand om met de data uit het voorbeeld te oefenen.

Alleen de stappen voor het uitvoeren van een one-way-ANOVA en two-way-ANOVA zijn uitgewerkt. Om een MANOVA of repeated measures ANOVA uit te voeren, kun je het beste de stappen voor de two-way-ANOVA volgen. Deze komen grotendeels overeen.

ANOVA-output interpreteren

Nadat de analyse is uitgevoerd krijg je SPSS-output terug. Deze verschilt voor de one-way-ANOVA en de two-way-ANOVA. Navigeer tussen de twee tabs om de output te bekijken.

• One-way-ANOVA
• Two-way-ANOVA

One-way-ANOVA interpreteren

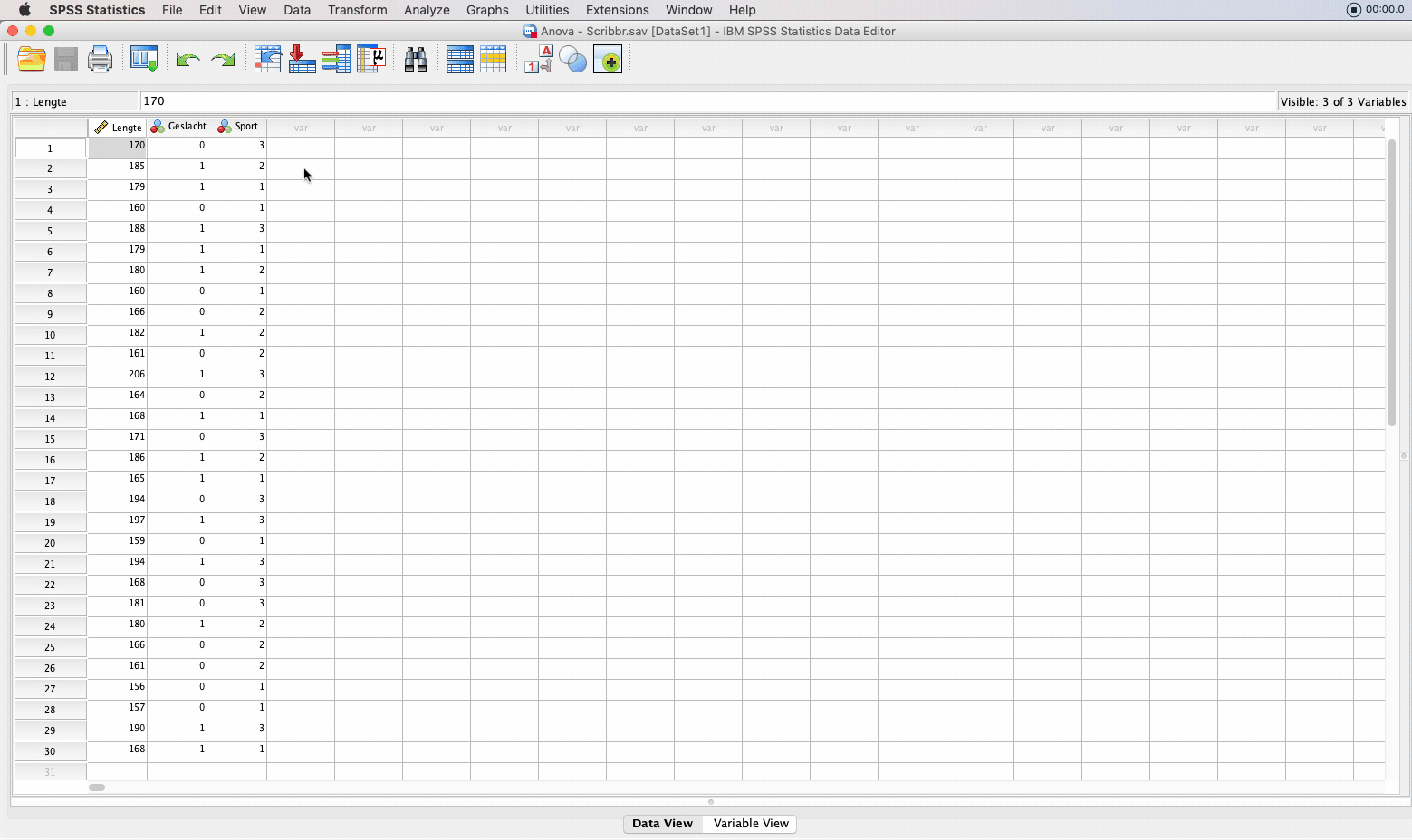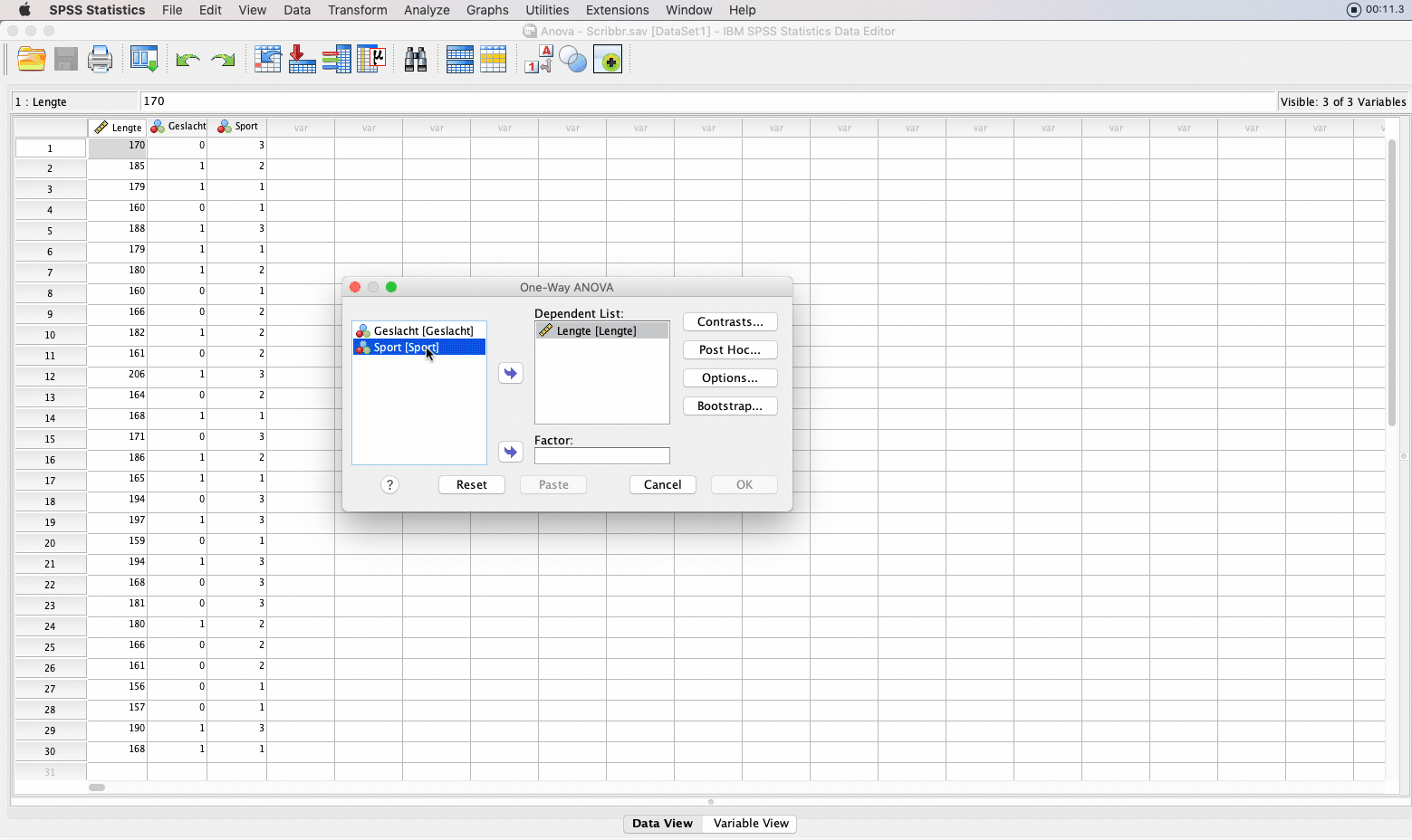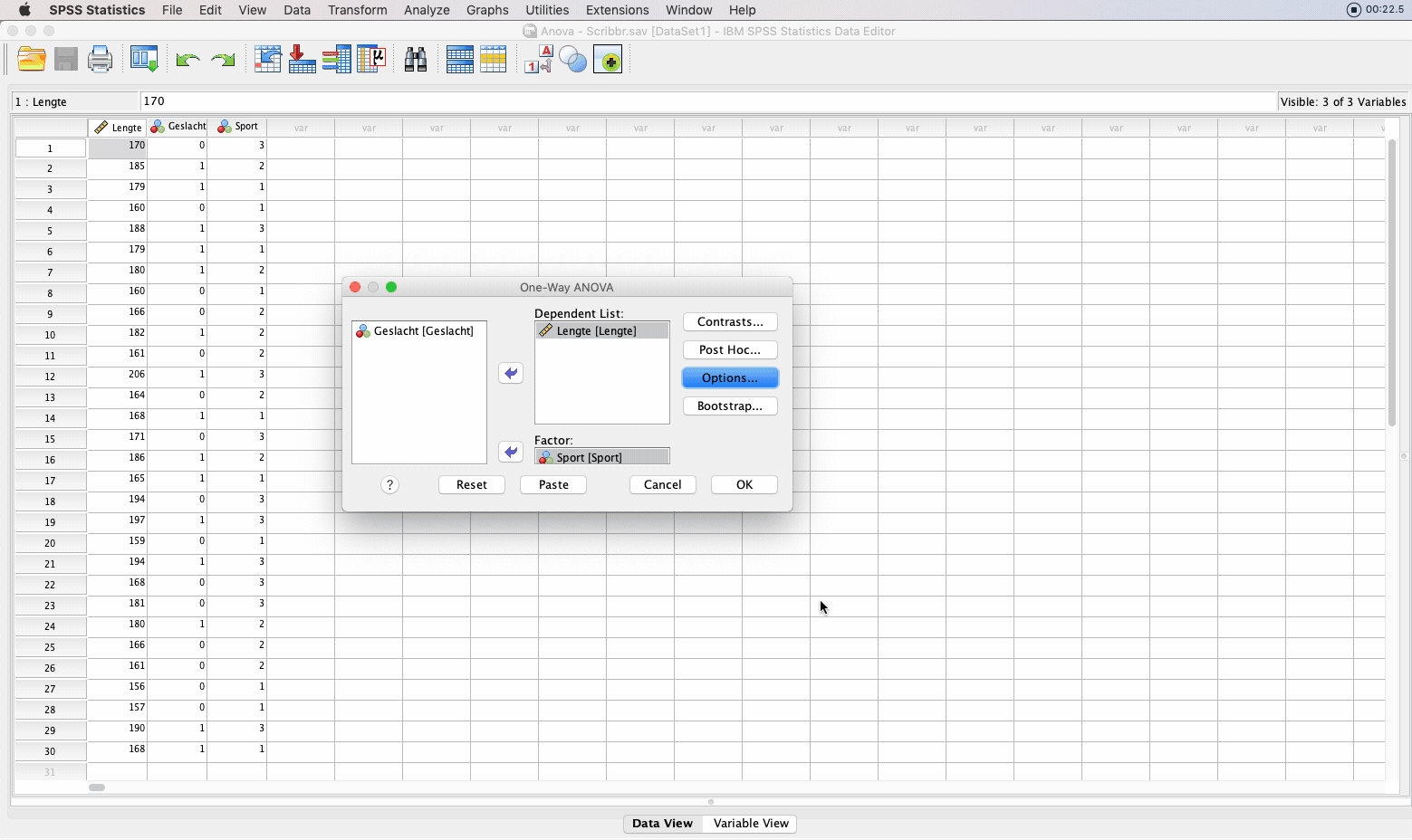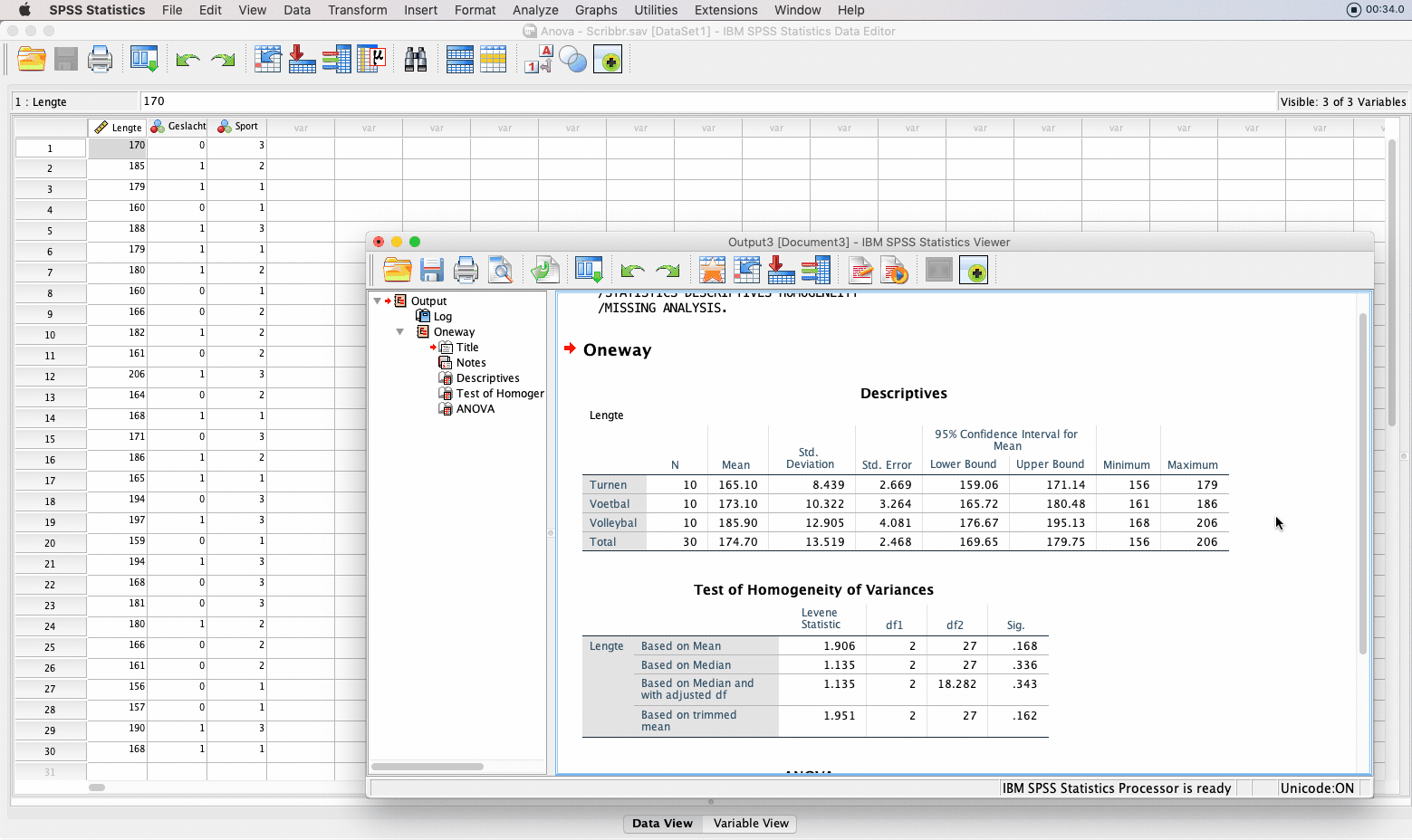
Als je ervoor hebt gekozen om ook voor gelijke varianties te testen krijg je twee tabellen: Test of homogeneity of variances’ en ‘ANOVA’.

Test of Homogeneity of Variances

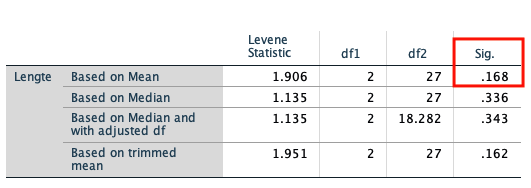
Op basis van de ‘test of homogeneity of variances’ kunnen we concluderen of aan de voorwaarde van gelijke varianties voor de verschillende groepen is voldaan. Je kijkt hierbij naar de Sig.-waarde van de rij ‘Based on Mean’. Is deze waarde groter dan ,050 dan zijn de varianties gelijk.

Als de varianties niet gelijk zijn voor de verschillende groepen dan is het beter om te kijken naar een robuuste test zoals de Welch of Brown-Forsythe, in plaats van de ANOVA.

ANOVA

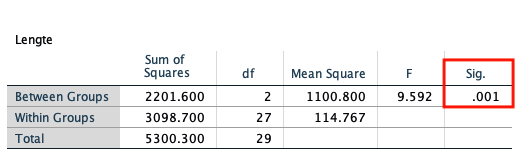
De tweede tabel is de ANOVA-tabel. Hier wordt getoetst of een significant deel van de variantie verklaard wordt door de groepsvariabele. Hiervoor wordt een F-toets uitgevoerd met vrijheidsgraden 2 (het aantal groepen (3) minus één) en 27 (het aantal observaties (30) minus het aantal groepen(3)).

De kans om een waarde van 9.592 of groter te observeren met deze vrijheidsgraden is .001, zoals af te lezen in de ‘Sig.’-kolom. Daarom kunnen we hier concluderen dat de groepsgemiddelden van elkaar verschillen.

De Sum of Squares geeft aan hoeveel van de variantie tussen (between) en binnen (within) de groepen zit. Hoe meer van de variantie tussen de groepen zit, hoe beter de groepen lengte voorspellen.

Two-way-ANOVA

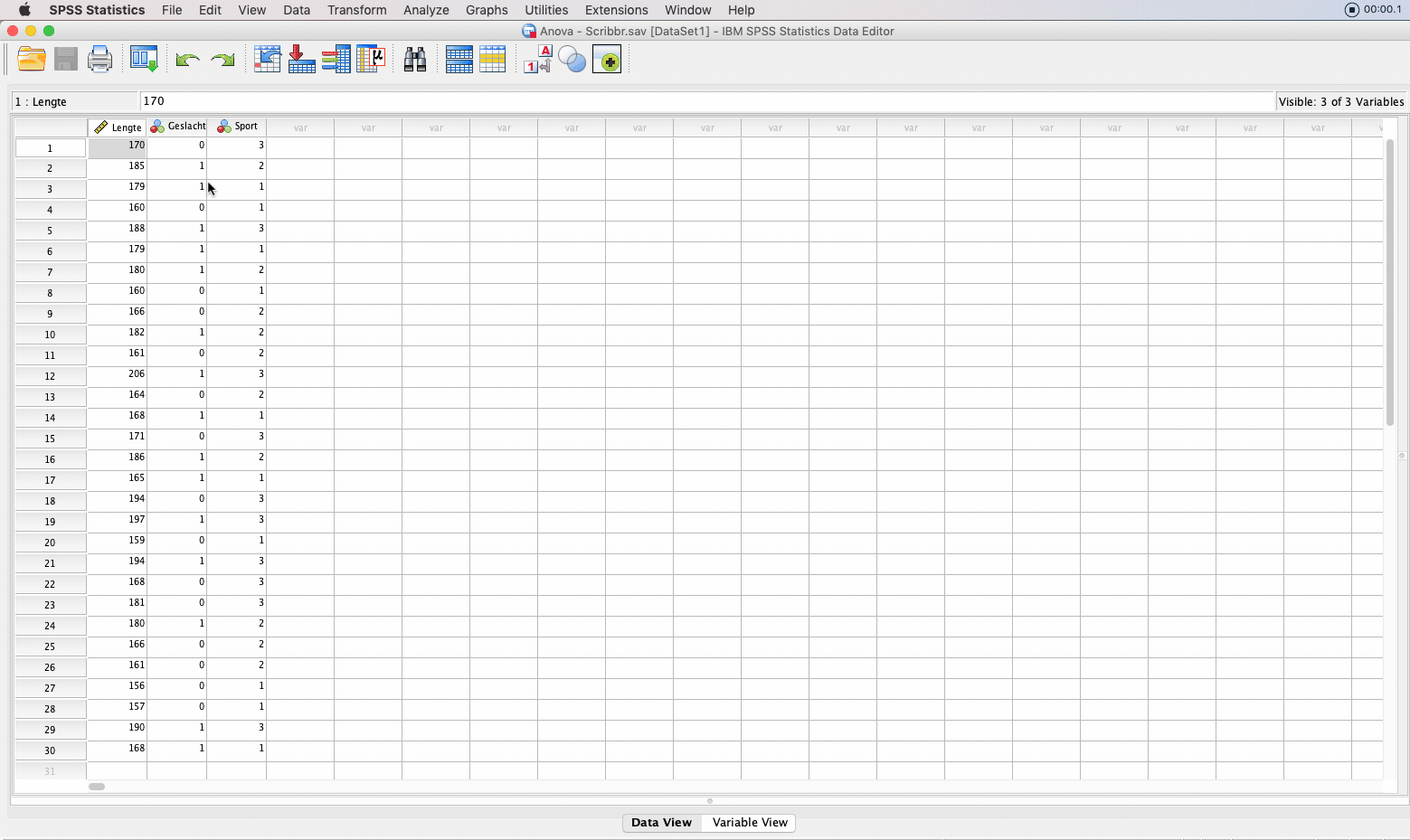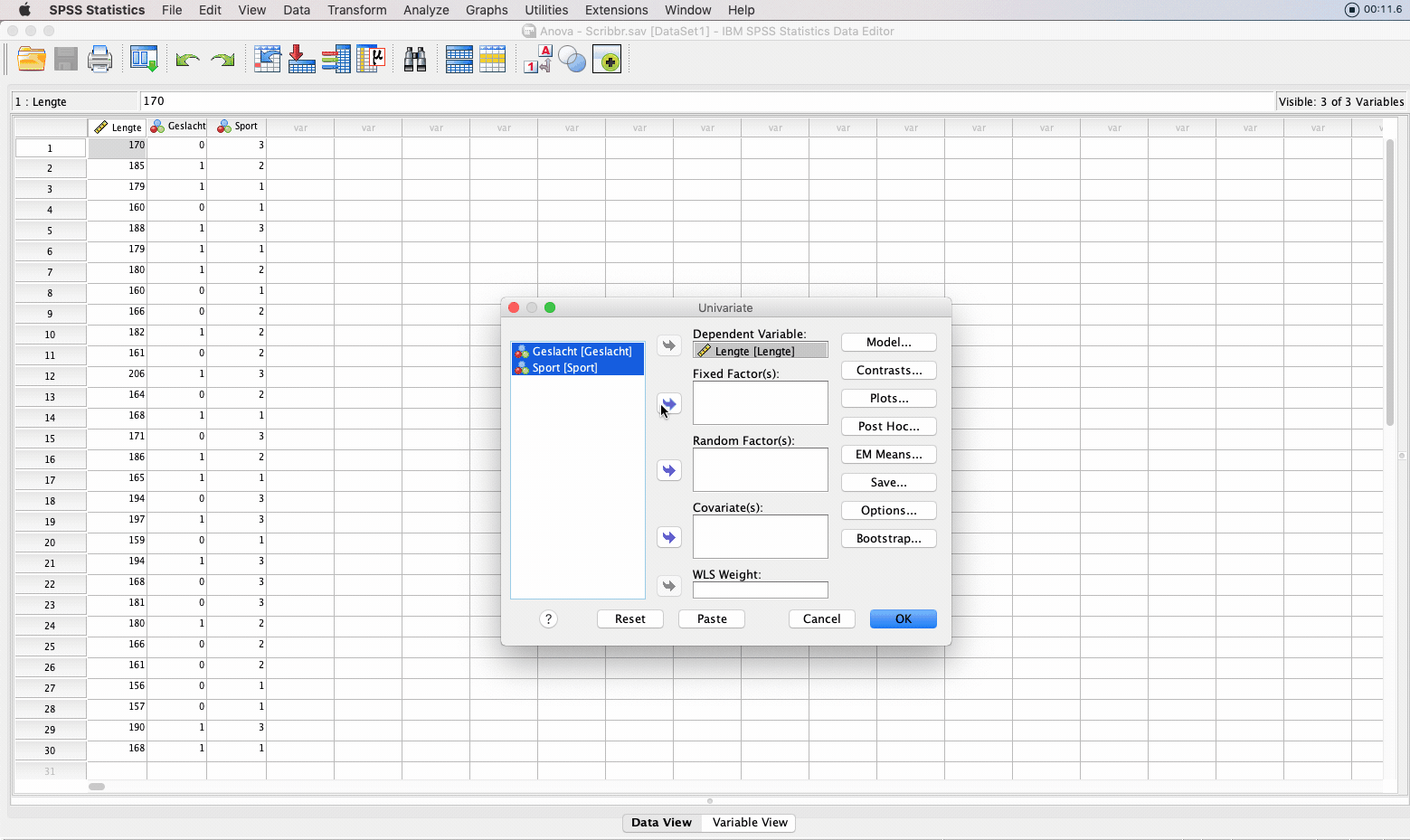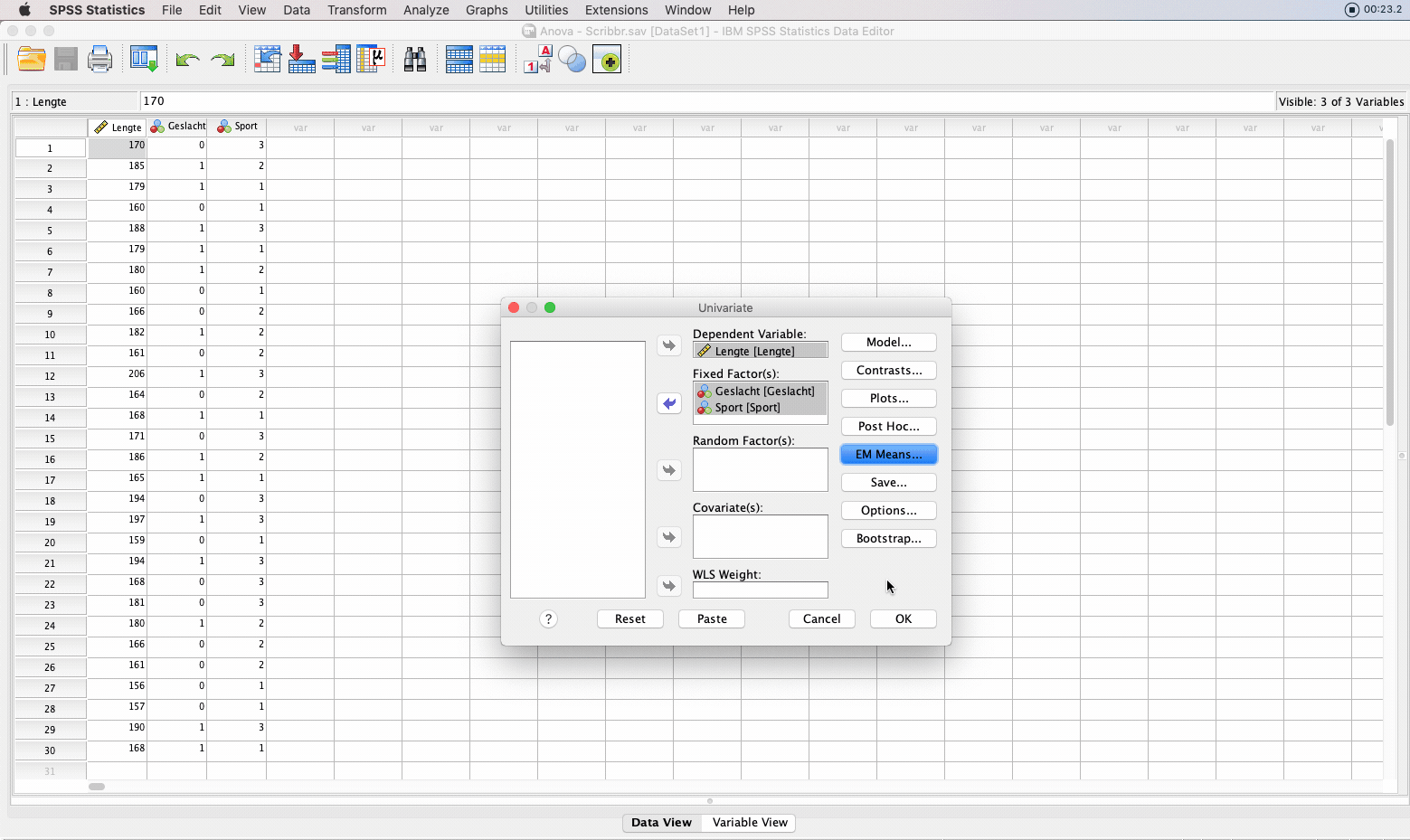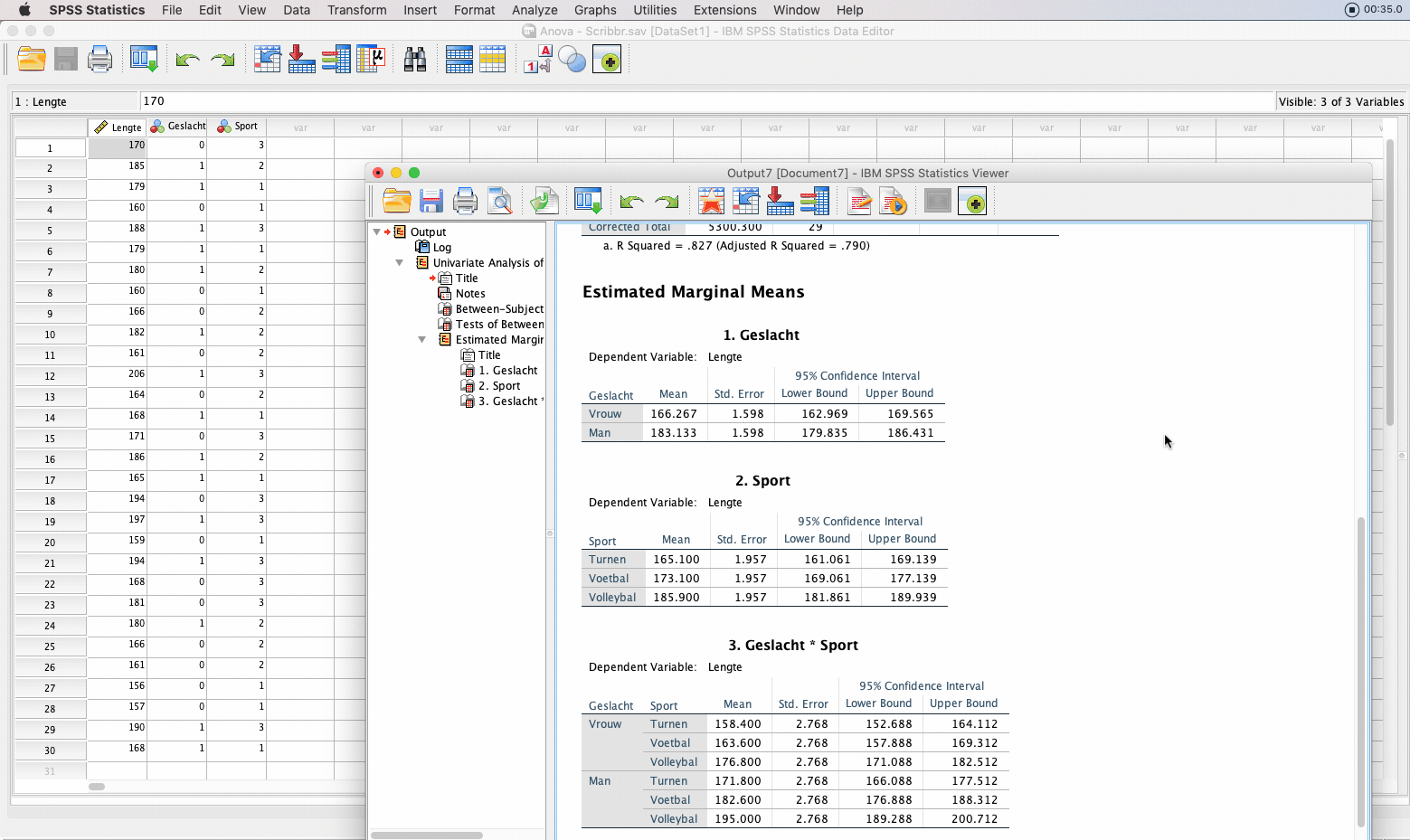
De output van de two-way-ANOVA bestaat uit een aantal tabellen met beschrijvende statistiek, zoals de gemiddelden voor elke groep. De belangrijkste tabel is de onderstaande ‘Tests of between-subjects effects’.

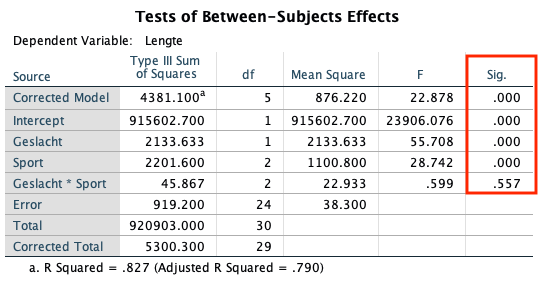
Er wordt getoetst of een significant deel van de variantie verklaard wordt door de groepsvariabelen. Hiervoor wordt een F-toets uitgevoerd met vrijheidsgraden 5 (het aantal groepen sporters (3) maal het aantal geslachten (2) minus één) en 24 (het aantal observaties (30) minus het aantal groepen sporters (3) maal het aantal geslachten (2)).

De kans om een waarde van 22.878 of groter te observeren met deze vrijheidsgraden is kleiner dan .001, zoals af te lezen in de ‘Sig.’-kolom. Daarom kunnen we hier concluderen dat de groepsgemiddelden van elkaar verschillen.

Zowel tussen de verschillende geslachten als tussen de sporters zijn er significante verschillen in de gemiddelde lengte, maar er is geen significant interactie-effect van geslacht op sport. Dat wil zeggen dat het verschil tussen sporters in lengte niet wordt beïnvloed door hun geslacht.

Post-hoc-tests

Je weet nu dat sommige groepen significant van elkaar verschillen. Om te weten welke groepen significant verschillen, kun je post-hoc-tests uitvoeren.

Dit doe je door opnieuw de ANOVA uit te voeren en op ‘Post Hoc’ te klikken. Je moet vervolgens kiezen tussen testen voor gelijke en ongelijke varianties.

Wanneer de varianties gelijk zijn wordt ‘Tukey’ vaak gebruikt. Wanneer de assumptie voor gelijke varianties niet is aangenomen dan wordt ‘Games-Howell’ vaak gebruikt. In onze dataset zijn de varianties gelijk bij de one-way-ANOVA (niet bij de two-way-ANOVA) en gebruiken we dus ‘Tukey’.

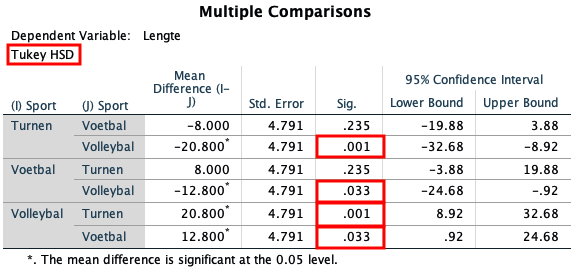
Je ziet nu dat er een extra tabel is toegevoegd aan de SPSS-output, namelijk de onderstaande ‘Post Hoc Tests’-tabel. Bekijk de Sig.-kolom en zoek naar de verschillen die significant zijn (p < .050).

De gemiddelde lengte verschilt significant tussen turners en volleyballers (p = .001) en tussen voetballers en volleyballers (p = .033). De gemiddelde lengte van voetballers en turners verschilt niet significant.

Resultaten ANOVA rapporteren

De resultaten van je ANOVA rapporteer je in het resultatenhoofdstuk van je scriptie. Je rapporteert de F-waarde met vrijheidsgraden en de bijbehorende significantie. Ook rapporteer je indien van toepassing de resultaten van de post-hoc-test. Enkele voorbeeldzinnen:

Er is een significant verschil in de gemiddelde lengte van de drie groepen sporters (F (2.27) = 9.952; p = .001). De post-hoc-Tukey-toets toont significante verschillen in lengte tussen volleyballers en voetballers (p = .033), en volleyballers en turners (p = .001). Er is geen significant verschil in lengte tussen turners en voetballers (p = .235).

Een ANOVA laat zien dat er een significant verschil in lengte is tussen de personen die verschillende sporten beoefenen, F (2.27) = 9.952; p = .001. Volleyballers zijn significant langer dan voetballers (p = .033) en turners (p = .001). Tussen turners en voetballers is geen significant verschil in lengte gevonden (p = .235).

Formule F-waarde

Hoewel programma’s als SPSS de ANOVA voor je kunnen uitvoeren, kan het soms ook handig zijn om zelf de formule te kennen. Stel dat er k groepen van groepsgrootte g zijn, dan is de F-waarde voor de one-way-ANOVA:

Hierbij staat g_j voor de groepsgrootte van groep j, en x̄_.j voor het gemiddelde van groep j.
Het aantal vrijheidsgraden van de F-waarde is gelijk aan de delers van teller en noemer, dus( k – 1) en (N – k).

Veelgestelde vragen

Wat is een ANOVA en waarvoor wordt de toets gebruikt?

ANOVA staat voor Analysis of Variance, oftewel variantieanalyse, en wordt gebruikt om gemiddelden van meer dan twee groepen met elkaar te vergelijken. Het is een uitbreiding van de t-toets, die het gemiddelde van maximaal twee groepen met elkaar vergelijkt.

Wat is een one-way ANOVA?

Je gebruikt een one-way-ANOVA wanneer één groepsvariabele (onafhankelijke variabele) de groepen bepaalt en er maar één afhankelijke variabele is.

Voorbeeld: Je vergelijkt de gemiddelde lengte van verschillende typen sporters, zoals voetballers, turners en volleyballers. Het type sport dat iemand beoefent, is in dit geval de enige groepsvariabele en lengte is de enige afhankelijke variabele.

Wat is een two-way ANOVA?

Je gebruikt een two-way-ANOVA (ook wel factorial ANOVA) als je twee of meer groepsvariabelen (onafhankelijke variabelen) in je conceptueel model hebt.

Voorbeeld: Je vergelijkt de gemiddelde lengte van verschillende typen sporters én hun gender. Er wordt dan niet alleen getest of het gemiddelde verschilt voor volleyballers en turners en voetballers, maar ook voor mannen, vrouwen en mensen met een ander gender, én of er eventuele interactie-effecten zijn.

Wat is een multivariate ANOVA (MANOVA)?

Je gebruikt een multivariate ANOVA (ook wel MANOVA) als je meerdere afhankelijke variabelen gebruikt. Je kunt deze ANOVA zowel gebruiken met één als meerdere groepsvariabelen (onafhankelijke variabelen).

Voorbeeld: Je wilt niet alleen niet alleen de gemiddelde lengte, maar ook het gemiddelde gewicht van verschillende groepen sporters vergelijken.

Je kunt beter een MANOVA uitvoeren dan meerdere losse ANOVA’s, om het risico op een Type I-fout te voorkomen.

Wat is een repeated measures ANOVA?

Je gebruikt een repeated measures ANOVA als je dezelfde groep respondenten meerdere malen onderzoekt (within-subjects design)

Voorbeeld: Je meet de gemiddelde lengte van respondenten in 2008, 2013, en 2018. Je vergelijkt dan de gemiddelde lengte van dezelfde persoon over een bepaalde periode om te kijken of deze verandert.