Interkwartielafstand (interquartile range) | Uitleg & voorbeelden

De interkwartielafstand (interquartile range) is een descriptieve statistiek die informatie geeft over de spreiding van de middelste helft van een verdeling. Deze maat behoort tot de vier meest gebruikte spreidingsmaten (measures of variability).

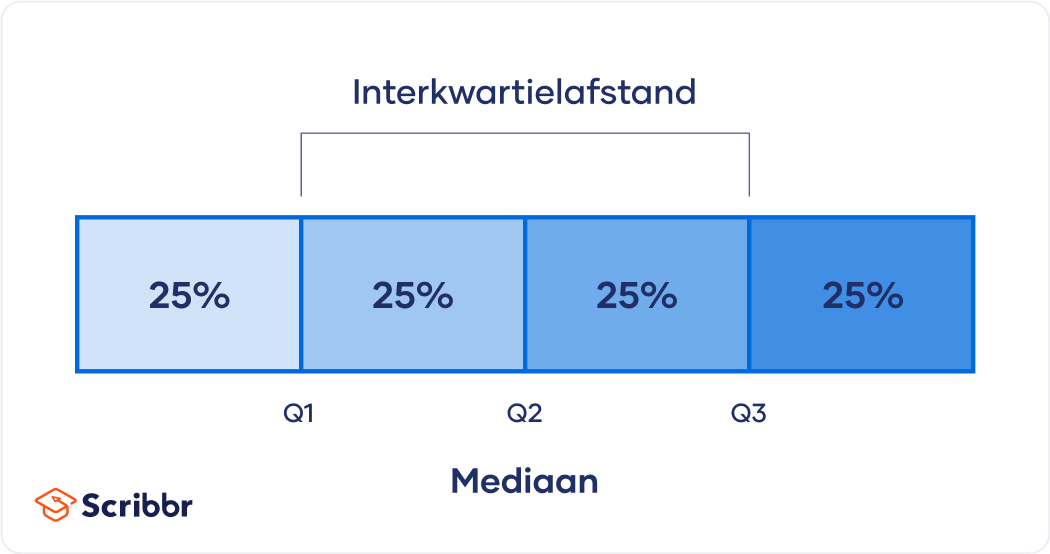
Iedere verdeling waarbij de waarden zijn gerangschikt van laag naar hoog kan worden verdeeld in vier gelijke delen (kwartielen). De interkwartielafstand (IQR) bevat het tweede en derde kwartiel, wat neerkomt op het middelste deel of de “middelste helft” van je dataset.

Het bereik (de range) geeft informatie over de spreiding in de gehele dataset, terwijl de interkwartielafstand gelijk is aan het bereik van de middelste helft.

Interkwartielafstand berekenen

Je kunt de interkwartielafstand met de hand berekenen of met behulp van onze interkwartielafstand calculator hieronder.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Bereken de interkwartielafstand

Je kunt de interkwartielafstand berekenen door de Q1-waarde van de Q3-waarde af te trekken:

Formule	Uitleg
	IQR = interkwartielafstand Q3 = 3e kwartiel (75e percentiel) Q1 = 1e kwartiel (25e percentiel)

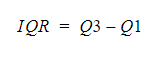Q1 is de grenswaarde waaronder 25% van de verdeling ligt, terwijl Q3 de grenswaarde is waaronder 75% van de verdeling ligt.

Je kunt Q1 zien als de mediaan van de eerste helft van de verdeling en Q3 als de mediaan van de tweede helft van de verdeling.

Methoden om de interkwartielafstand te bepalen

Hoewel er maar één formule is, zijn er verschillende methoden om de kwartielen te bepalen. Iedere methode levert een andere waarde op voor de interkwartielafstand.

In dit artikel bespreken we twee van de meest gebruikte methoden. Het verschil tussen de methoden is de manier waarop de mediaan wordt gebruikt.

Exclusieve methode vs inclusieve methode

Voor de exclusieve methode sluit je de mediaan uit om Q1 en Q3 te bepalen, terwijl je mediaan meeneemt in de berekening bij de inclusieve methode.

De procedure om de mediaan te vinden is afhankelijk van het aantal waarden in de dataset (een even of oneven aantal).

• Als je een oneven aantal waarden hebt, is de mediaan de middelste waarde in je dataset. Je kunt in dit geval kiezen tussen de inclusieve en exclusieve methode.
• Als je een even aantal waarden hebt, zijn er twee waarden in het midden, en is de mediaan het gemiddelde van die twee waarden. In dit geval is het gebruikelijker om de exclusieve methode te gebruiken.

De exclusieve interkwartielafstand is altijd groter dan de inclusieve interkwartielafstand.

Er is geen overeenstemming over de beste methode, maar meestal wordt gekeken naar de steekproefgrootte. De exclusieve methode is vaak geschikter voor grote steekproeven, terwijl de inclusieve methode beter is voor kleine steekproeven (vanwege het kleinere bereik).

Stappenplan voor de exclusieve methode

Om het stappenplan voor de exclusieve methode uit te leggen, gebruiken we twee voorbeelden: een dataset met een even aantal waarden en een dataset met een oneven aantal waarden.

Dataset met een even aantal waarden

We volgen het stappenplan aan de hand van een voorbeeld-dataset met 10 waarden.

Stap 1: Rangschik de waarden van laag naar hoog.
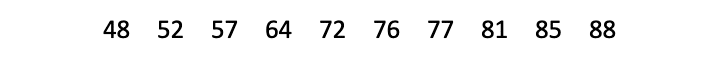Stap 2: Bepaal de mediaan en scheid de waarden onder en boven de mediaan.
Bij een dataset met een even aantal waarden is de mediaan het gemiddelde van de twee waarden in het midden, dus je kunt de dataset eenvoudig in twee helften verdelen.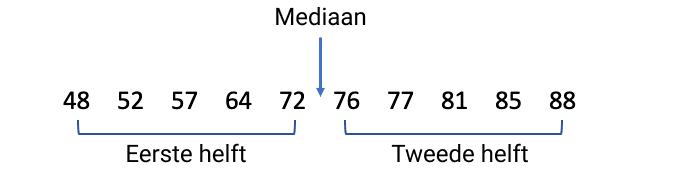
Stap 3: Bepaal Q1 en Q3.
Q1 is de mediaan van de eerste helft en Q3 is de mediaan van de tweede helft. Aangezien elk van deze helften een oneven aantal waarden heeft, is er slechts één waarde in het midden van elke helft.
Stap 4: Bereken de interkwartielafstand.

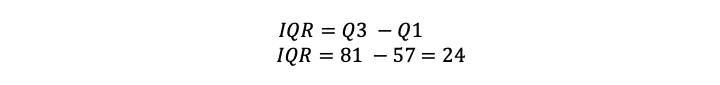Dataset met een oneven aantal waarden

In dit voorbeeld gebruiken we een dataset met 11 waarden.

Stap 1: Rangschik de waarden van laag naar hoog.
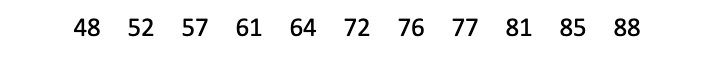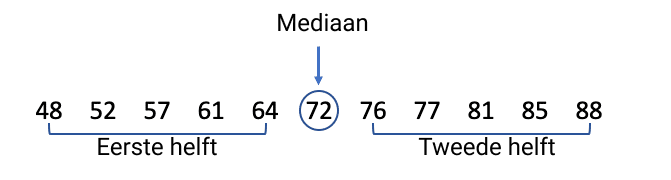
Stap 2: Bepaal de mediaan en scheid de waarden onder en boven de mediaan.
In een dataset met een oneven aantal waarden is de mediaan het getal in het midden van de lijst. De mediaan zelf is uitgesloten van beide helften: de ene helft bevat alle waarden onder de mediaan en de andere bevat alle waarden erboven.
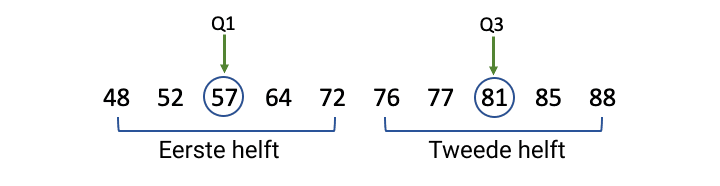
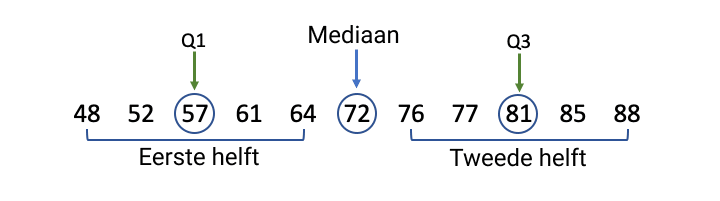
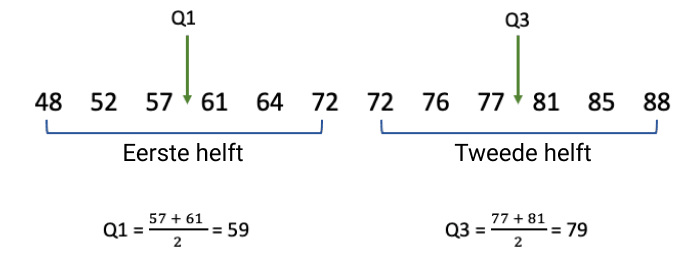
Stap 3: Bepaal Q1 en Q3.
Q1 is de mediaan van de eerste helft en Q3 is de mediaan van de tweede helft. Aangezien elk van deze helften een oneven aantal waarden heeft, is er slechts één waarde in het midden van elke helft.
Stap 4: Bereken de interkwartielafstand.

Ontvang feedback op taal, structuur, lay-out en bronvermelding

Professionele Scribbr-editors kijken je scriptie na op:

• Academisch taalgebruik
• Onduidelijke zinnen
• Grammaticale fouten
• Interpunctie
• Verboden woorden

Bekijk het voorbeeld

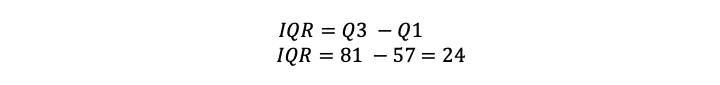Stappenplan voor de inclusieve methode

Het stappenplan voor de inclusieve methode is bijna hetzelfde als dat voor de exclusieve methode. Het verschil zit hem in de manier waarop de dataset in twee helften is verdeeld.

Stap 1: Rangschik de waarden van laag naar hoog.
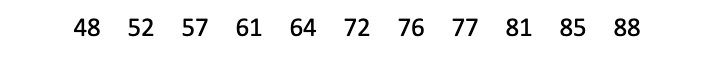Stap 2: Bepaal de mediaan.
De mediaan is de middelste waarde in de dataset.
Stap 2: Deel de lijst op in twee helften, waarbij de mediaan tot beide helften behoort.
De mediaan is de hoogste waarde in de eerste helft en de laagste waarde in de tweede helft.
Stap 3: Bepaal Q1 en Q3.
Q1 is de mediaan van de eerste helft en Q3 is de mediaan van de tweede helft. Aangezien de twee helften elk een even aantal waarden bevatten, zijn Q1 en Q3 het gemiddelde van de middelste waarden.
Stap 4: Bereken de interkwartielafstand.

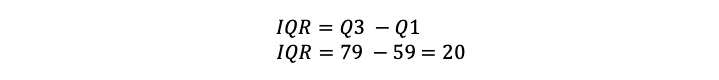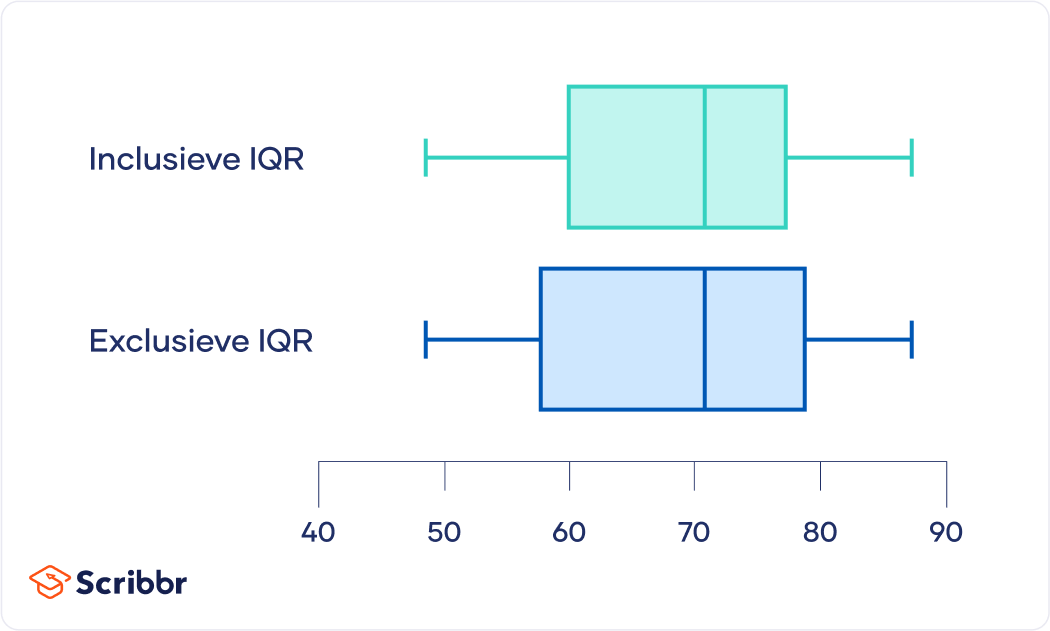
We kunnen aan deze voorbeelden zien dat het gebruik van de inclusieve methode een kleinere IQR geeft dan de exclusieve methode. Met dezelfde dataset is de exclusieve IQR 24 en de inclusieve IQR 20.

Wanneer gebruik je de interkwartielafstand?

De interkwartielafstand is een hele handige spreidingsmaat in het geval van scheve verdelingen. Voor deze verdelingen is de mediaan de beste centrummaat, omdat de mediaan precies de middelste waarde is (als de waarden van laag naar hoog zijn gerangschikt).

De mediaan en IQR kunnen inzicht geven in de clustering van waarden. Ook is de IQR geschikt voor datasets met uitbijters. De spreidingsmaat is gebaseerd op de middelste helft van de verdeling, waardoor deze minder gevoelig is voor extreme waarden (die zich aan de uiteinden bevinden).

Visualiseer de interkwartielafstand met boxplots

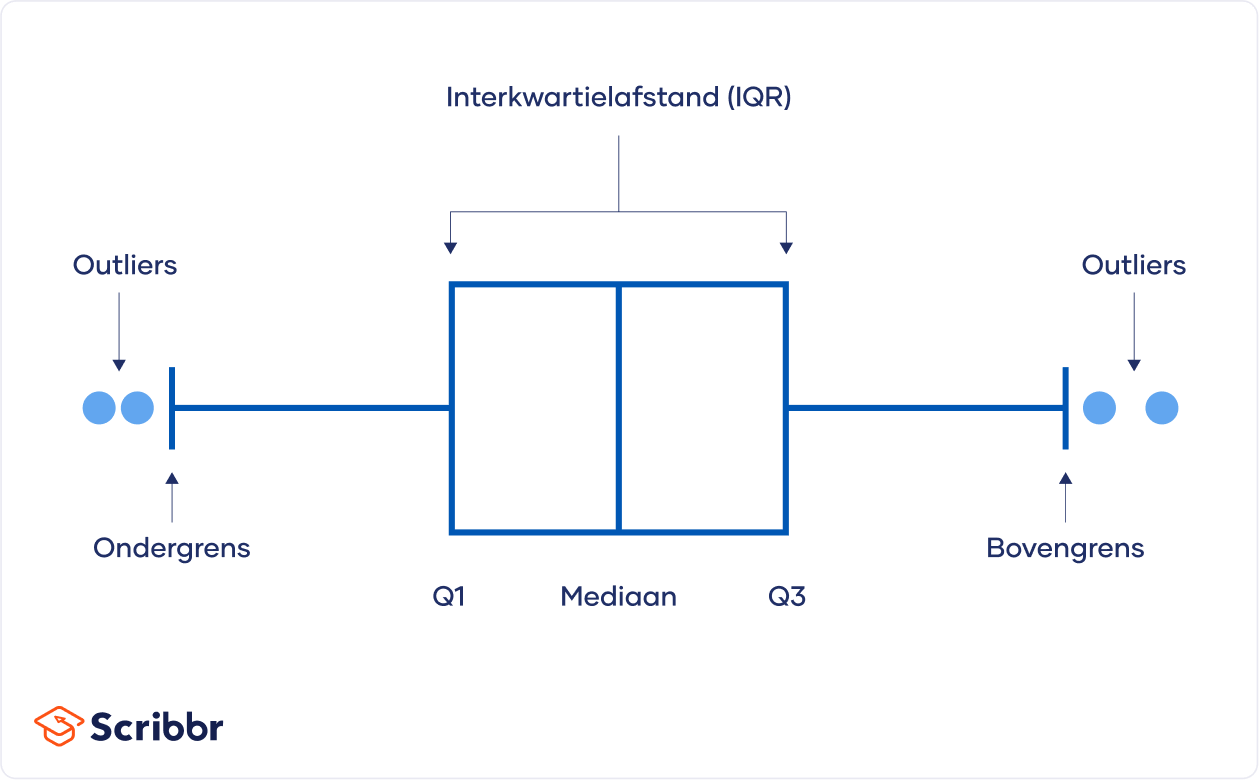
Een boxplot (ook wel een whisker plot genoemd) visualiseert een dataset met behulp van vijf samenvattende waarden:

• Laagste waarde
• Q1: 25e percentiel
• Mediaan
• Q3: 75e percentiel
• Hoogste waarde

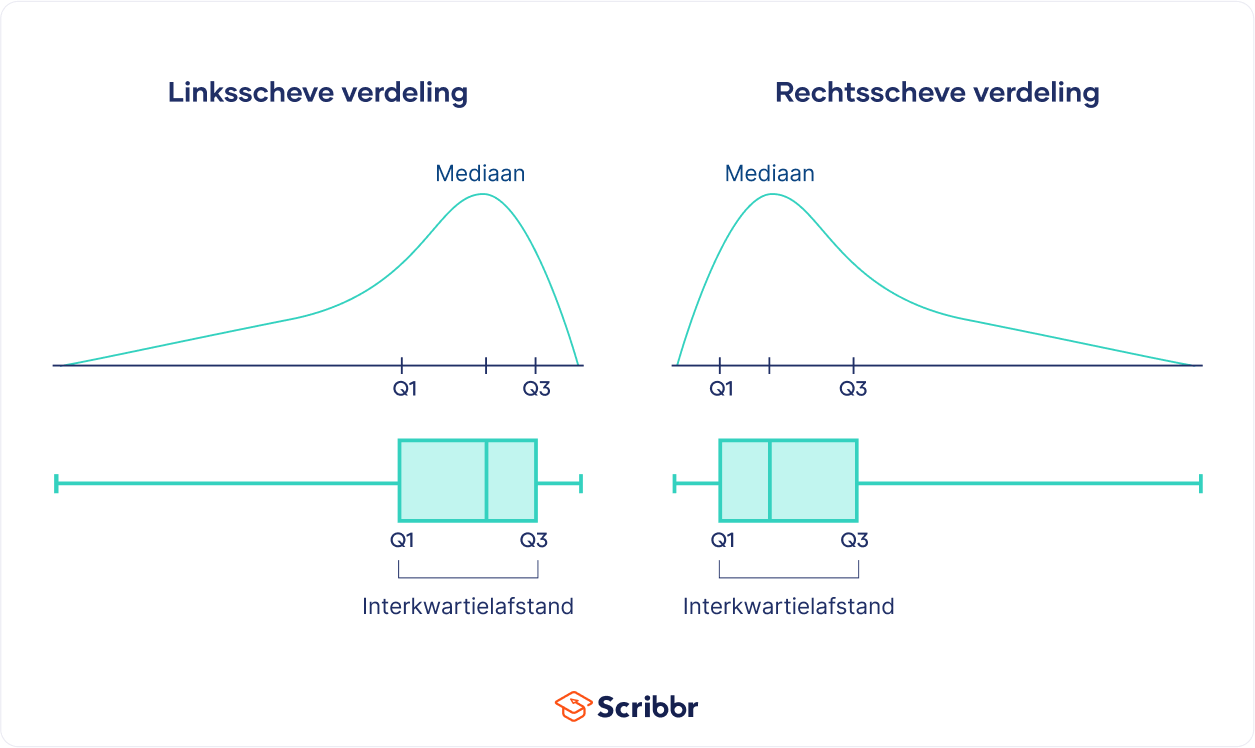
De verticale lijnen in de box staan voor Q1, de mediaan en Q3, terwijl de verticale lijnen aan de uiteinden (de “snorharen”) de hoogste en laagste waarden weergeven.

De breedte van de box geeft de interkwartielafstand weer. Een smallere box betekent dat er minder spreiding is, terwijl een bredere box betekent dat er meer spreiding is.

De box voor een inclusieve IQR is smaller dan een box voor een exclusieve IQR.

Boxplots zijn handig om de centrale tendens en spreiding van scheve verdelingen te visualiseren.

De plaatsing van de box op de horizontale lijn laat de richting van de scheve verdeling zien. Als de box dichter bij de rechterkant staat, is er sprake van een linksscheve of negatiefscheve verdeling. Als de box dichter bij de linkerkant staat, is er sprake van een rechtsscheve of positiefscheve verdeling.

Veelgestelde vragen

Wat is het verschil tussen het bereik en de interkwartielafstand?

Het bereik geeft je de spreiding van de gehele dataset, terwijl de interkwartielafstand je de spreiding van de middelste helft van de dataset geeft.

Wat zijn de vier meest gebruikte spreidingsmaten?

De spreiding (variability) wordt meestal bepaald met de volgende descriptieve statistieken:

• Bereik (range): het verschil tussen de hoogste en laagste waarde uit de dataset.
• Interkwartielafstand (interquartile range): het bereik van het middelste deel van de dataset.
• Standaarddeviatie (standard deviation): de gemiddelde afstand tussen iedere waarde in de dataset en het gemiddelde.
• Variantie (variance): de standaarddeviatie in het kwadraat.

Wanneer moet je de interkwartielafstand gebruiken?

De interkwartielafstand is de beste spreidingsmaat voor scheve verdelingen of datasets met uitbijters (ook wel uitschieters of outliers genoemd).

De maat is gebaseerd op waarden uit de middelste helft van de dataset, waardoor het onwaarschijnlijk is dat de interkwartielafstand wordt beïnvloed door extreme waarden.