Regressieanalyse uitvoeren, interpreteren en rapporteren

Regressieanalyse wordt gebruikt om het effect te bepalen van een (of meerdere) verklarende variabele(n), zoals lengte of leeftijd, op een afhankelijke variabele zoals gewicht.

Je kunt regressieanalyse gebruiken om:

1. Samenhang tussen twee variabelen te bepalen (leeftijd en waarde van een auto)
2. Verandering van de afhankelijke variabele te voorspellen (waarde van een auto naarmate deze ouder wordt)
3. Toekomstige waarde te voorspellen (waarde van een zes jaar oude auto)

Soorten regressieanalyse

Er bestaan meerdere soorten regressieanalyses, namelijk:

• Enkelvoudige regressie
• Meervoudige regressie
• Logistische regressie

Welke soort je gebruikt hangt af van het aantal variabelen dat je wilt testen en het meetniveau (nominaal, ordinaal, interval of ratio) waarop deze variabelen gemeten zijn. In dit artikel behandelen we alleen lineaire enkelvoudige en meervoudige regressie.

Deze soorten regressie kun je gebruiken voor één of meerdere verklarende variabelen en een afhankelijke variabele op interval of rationiveau.

Enkelvoudige regressie

Als je het effect van één verklarende (of onafhankelijke) variabele op een afhankelijke variabele wilt testen dan gebruik je enkelvoudige regressie.

Voorbeeld: Je wilt aan de hand van lengte (verklarende variabele X) iemands gewicht (afhankelijke variabele Y) voorspellen of verklaren.

Een enkelvoudige regressie kan worden uitgedrukt met de volgende vergelijking:

Y = α + βX + u

Deze vergelijking bestaat uit drie elementen:

1. Intercept (α) is het startpunt van de regressielijn; de zogenaamde ‘constante’. Dit betekent dat zelfs als de lengte 0 cm is, er nog wel een bepaald basisgewicht is.
2. Regressiecoëfficiënt (β) geeft de gemiddelde toename in Y (gewicht) aan wanneer de verklarende variabele X (lengte) met 1 (centimeter) toeneemt.
3. Foutterm (u) ofwel de storingsterm. Dit is het deel van de afhankelijke variabele dat niet verklaard kan worden door de verklarende variabele.

Meervoudige regressie

Meervoudige of multipele regressie is een uitbreiding van de enkelvoudige regressie waarbij twee of meer verklarende variabelen worden gebruikt om de afhankelijke variabele (Y) te voorspellen of verklaren.

Voorbeeld: Je wilt naast lengte ook geslacht gebruiken om iemands gewicht te voorspellen. In dit geval voeg je geslacht als tweede variabele X₂ toe.

De regressievergelijking ziet er nu als volgt uit:

Υ = α + β₁X₁ + β₂X₂ + u

Het enige verschil in deze vergelijking ten opzichte van de enkelvoudige regressie is dat er een tweede regressiecoëfficiënt (β) is toegevoegd voor de verklarende variabele ‘geslacht’.

Assumpties regressieanalyse

Om door middel van lineaire regressie tot een goede schatting van de regressiecoëfficiënten te komen, moet de data aan enkele voorwaarden voldoen.

• De relatie tussen de verklarende en afhankelijke variabelen is lineair
• De data zijn verkregen uit een willekeurige steekproef van de populatie
• De verklarende variabelen die je opneemt in de regressie hebben geen lineair verband
• Exogeniteit: de verwachte foutterm is nul
• Homoscedasticiteit: de variantie van de foutterm is gelijk voor alle waarden van de verklarende variabele.

Regressieanalyse uitvoeren met SPSS of Excel

Om een regressieanalyse uit te voeren kun je gebruikmaken van programma’s zoals SPSS en Excel. Met uitleg en een GIF lopen we door de stappen heen. Gebruik de tabs om te navigeren tussen de uitleg voor SPSS en Excel.

Regressieanalyse interpreteren

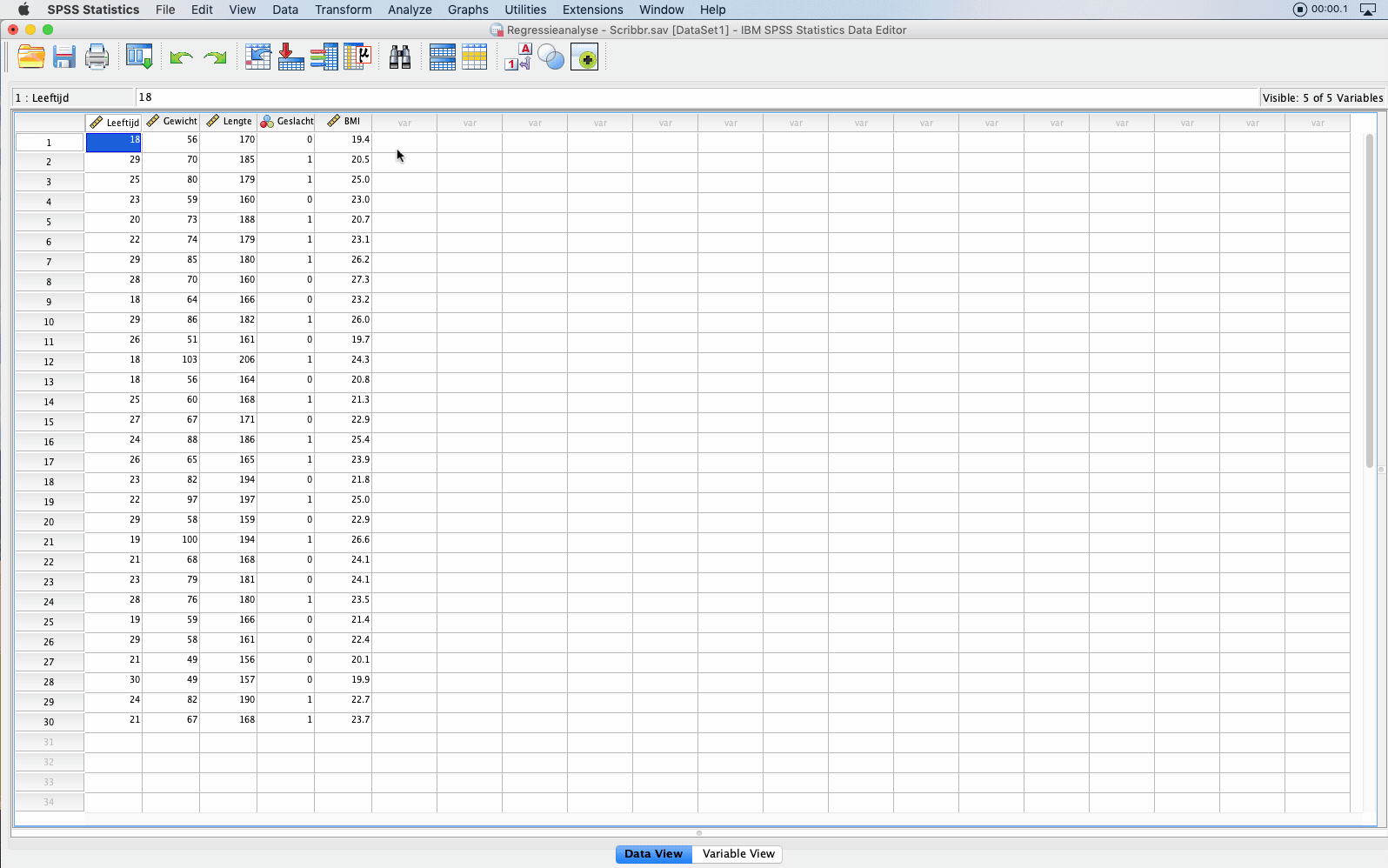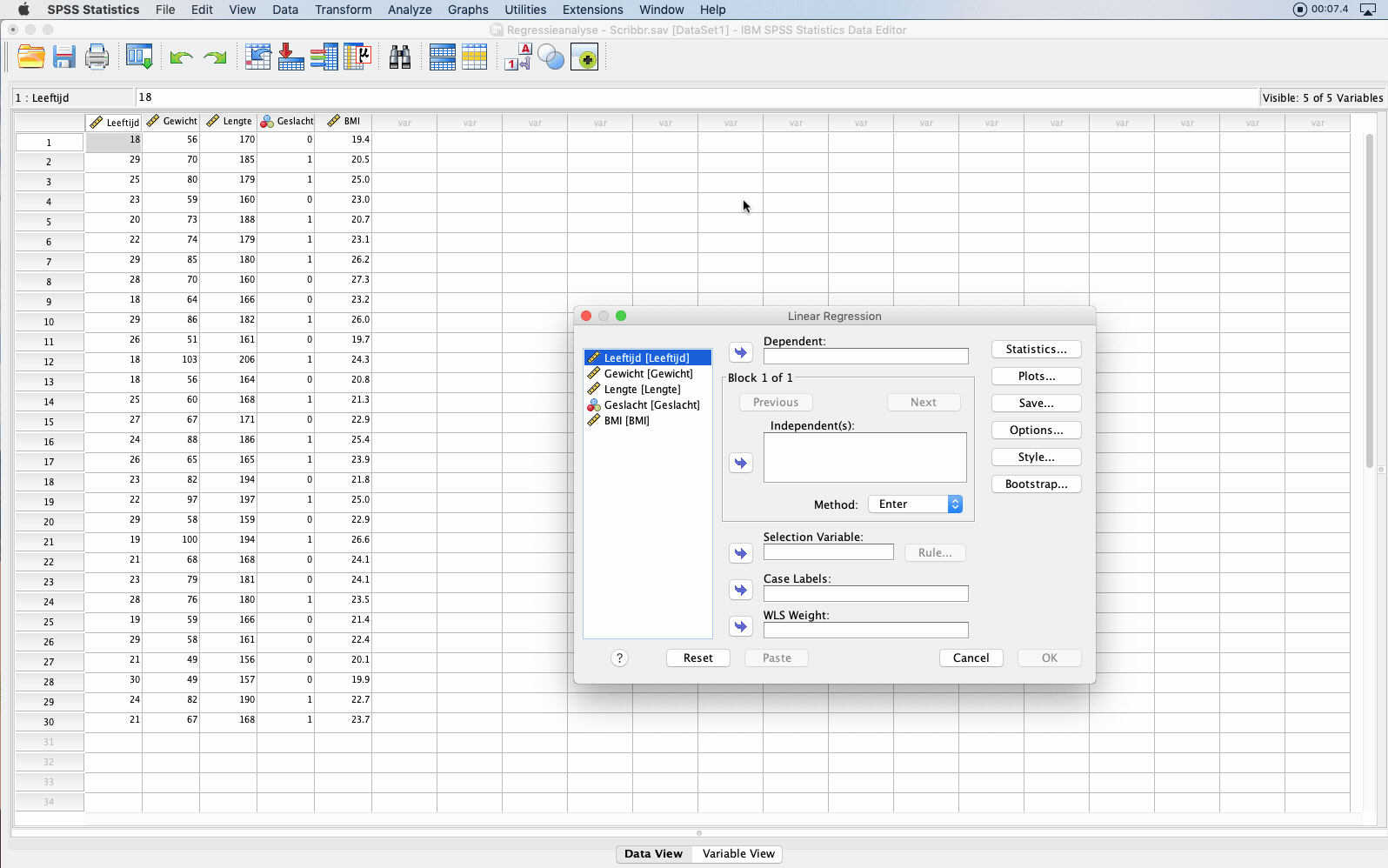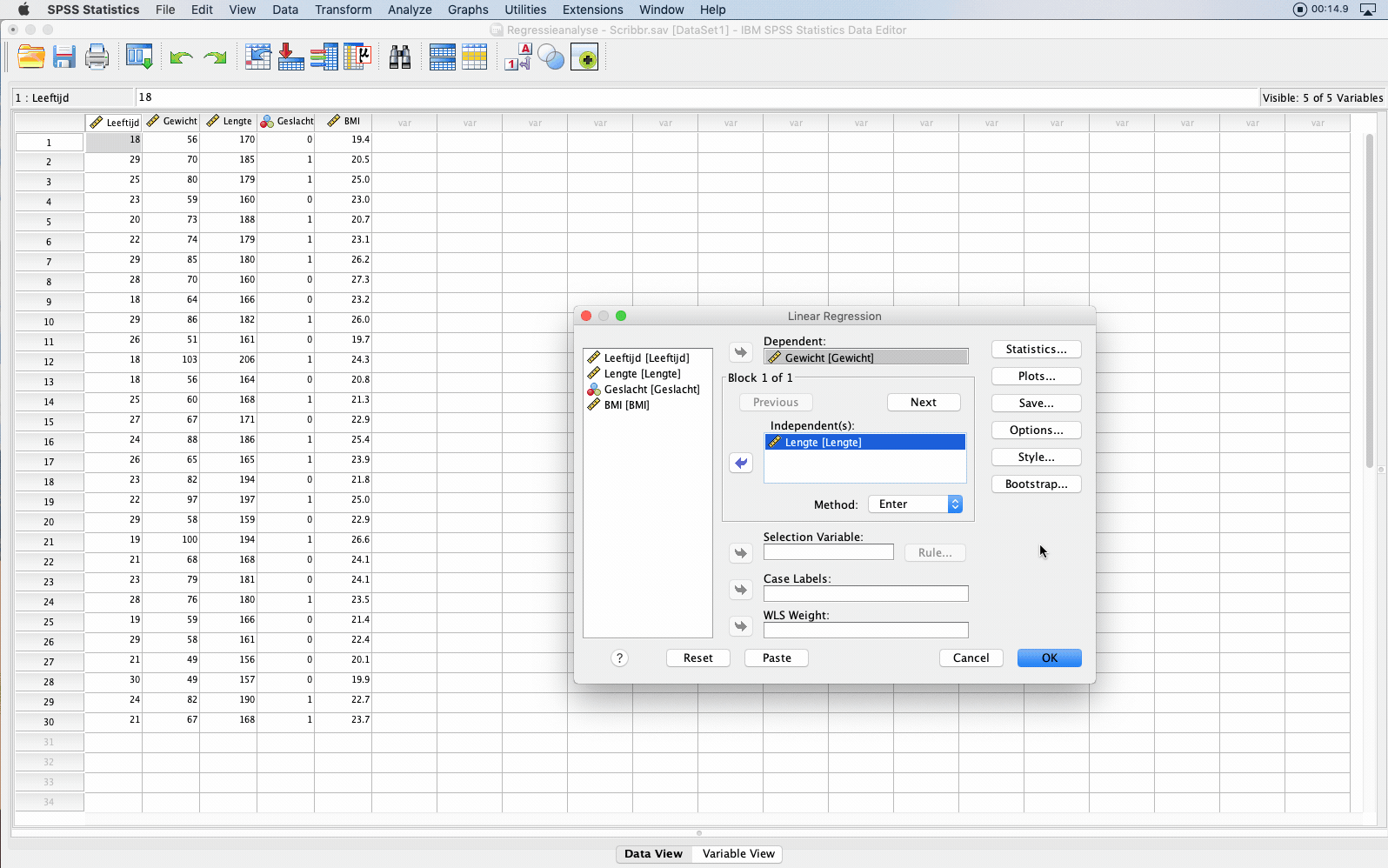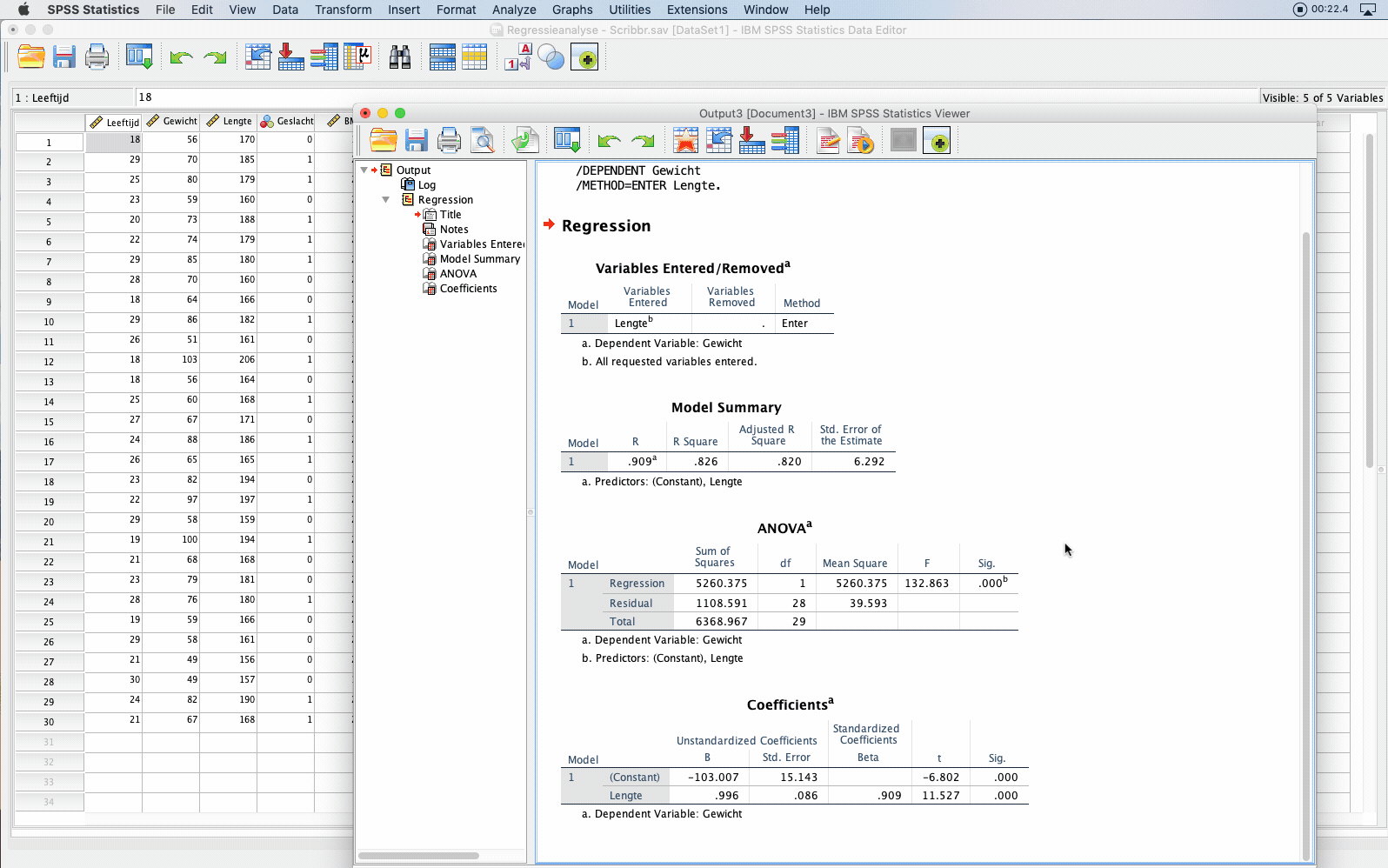
De output van een regressieanalyse bestaat uit drie onderdelen, namelijk de ‘model summary’, ‘ANOVA’ en ‘Coefficients’. Voor dit voorbeeld hebben we de SPSS-output genomen, maar deze lijkt erg op die van Excel.

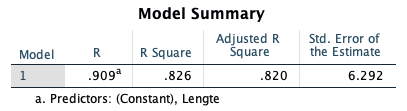
Het eerste blok, model summary, vermeldt de correlatiecoëfficiënt R en de determinatiecoëfficiënt R² . De correlatiecoëfficiënt is in dit voorbeeld zeer hoog, namelijk ,909.

De ‘R Squared’ geeft aan hoeveel van de variantie in de afhankelijke variabele (gewicht) verklaard wordt door de verklarende variabelen.

De R Squared heeft altijd een waarde tussen 0 en 1 waarbij 1 het best mogelijke model aangeeft waarbij alle variantie in de afhankelijke variabele verklaard wordt. In dit voorbeeld verklaart de variabele ‘lengte’ voor 82,6% iemands gewicht.

Als je een meervoudige regressie uitvoert kijk je naar de ‘Adjusted R Square’ in plaats van ‘R Square’ omdat meer verklarende variabelen altijd meer van de variantie kunnen verklaren. De adjusted R² corrigeert hiervoor.

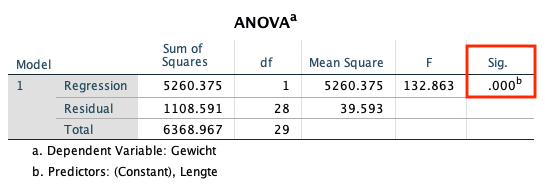
Het tweede blok, ANOVA, toetst de significantie van het regressiemodel. Dat laat zien hoe groot de kans is dat alle regressiecoëfficiënten in werkelijkheid nul zijn en de uitkomsten van deze analyse dus op toeval berusten.

Hiervoor wordt een F-toets uitgevoerd met vrijheidsgraden 1 (het aantal verklarende variabelen) en 28 (het aantal observaties minus het aantal verklarende variabelen minus één).

De kans om een waarde van 132,863 of groter te observeren met deze vrijheidsgraden is kleiner dan .001, zoals af te lezen in de ‘Sig.’-kolom. Daarom kunnen we concluderen dat dit regressiemodel significante verklarende variabelen bevat.

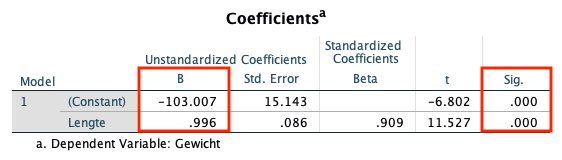
De ‘coefficients’-tabel geeft informatie over de grootte, de aard (plus of minus) en de significantie van het effect van de verklarende variabelen op de afhankelijke variabele.

De regressielijn volgt de vergelijking Gewicht  =  -103,007 + 0,996 * Lengte. Het geschatte gemiddelde effect van een toename van één centimeter in lengte is dus 996 gram.

Om te testen of dit effect significant is, wordt er een t-toets uitgevoerd. De kans om een waarde van 11,527 of groter te observeren is kleiner dan .0001, zoals af te lezen in de ‘Sig.’-kolom. Daarom is dit effect significant.

Voorbeeld: Een man van 180 cm lang wordt geschat op 76,27 kg.: -103,007 + 0,996 * 180 = 76,27 kg.

Bij meervoudige regressie is de regressiecoëfficiënt de gemiddelde toename van de afhankelijke variabele, terwijl de andere verklarende variabelen gelijk blijven.

Regressie rapporteren

De uitkomsten van de regressieanalyse rapporteer je in het resultatenhoofdstuk van je scriptie. Je rapporteert in ieder geval:

• De verklaarde variantie van je regressiemodel (R² of R Squared)
• De F-waarde en de significantie van je regressiemodel
• De regressiecoëfficiënt en zijn significantie

Je kunt een van de volgende zinnen gebruiken:

Een enkelvoudige regressie met gewicht als afhankelijke variabele en lengte als verklarende variabele is significant, F (1.28) = 132.86, p  < .001.

82,6% van de variantie in gewicht kon worden verklaard met lengte. De regressiecoëfficiënt van lengte was 0.996 en significant (t (28) = 11.53; p < .001).

Lengte is een significante voorspeller van gewicht. De voorspelde toename in gewicht is 996 gram per centimeter (β = 0.909; t (28) = 11.53; p < .001). Lengte verklaart ook een significant deel van de variantie in gewicht (R² = .826; F (1.28) = 132.86; p < .001).

Voor het rapporteren van statistische resultaten heeft de APA-stijl verschillende richtlijnen opgesteld. Zo weet je precies wanneer je symbolen of variabelen cursief, vet of romein schrijft en met hoeveel decimalen je de significantie rapporteert.

Veelgestelde vragen

Wat is een regressieanalyse en waarvoor wordt deze gebruikt?

Regressieanalyses worden gebruikt om het effect te bepalen van een (of meerdere) verklarende variabele(n), zoals lengte of leeftijd, op een afhankelijke variabele zoals gewicht.

Je kunt regressieanalyse gebruiken om:

1. Samenhang tussen twee variabelen te bepalen (leeftijd en waarde van een auto)
2. Verandering van de afhankelijke variabele te voorspellen (waarde van een auto naarmate deze ouder wordt)
3. Toekomstige waarde te voorspellen (waarde van een zes jaar oude auto)

Wanneer gebruik je een enkelvoudige regressieanalyse?

Je gebruikt een enkelvoudige regressieanalyse als je het effect van één verklarende (of onafhankelijke) variabele op een afhankelijke variabele wilt testen.

Voorbeeld: Je wilt aan de hand van lengte (verklarende variabele X) iemands gewicht (afhankelijke variabele Y) voorspellen of verklaren.

Een enkelvoudige regressie kan worden uitgedrukt met de volgende vergelijking:

Y = α + βX + u

Wanneer gebruik je een meervoudige regressieanalyse?

Een meervoudige of multipele regressieanalyse is een uitbreiding van de enkelvoudige regressie waarbij twee of meer verklarende variabelen worden gebruikt om de afhankelijke variabele (Y) te voorspellen of verklaren.

Voorbeeld: Je wilt naast lengte ook geslacht gebruiken om iemands gewicht te voorspellen. In dit geval voeg je geslacht als tweede variabele X₂ toe.

De regressievergelijking ziet er als volgt uit:

Υ = α + β₁X₁ + β₂X₂ + u