Boxplot maken en aflezen | Stappenplan & Voorbeelden

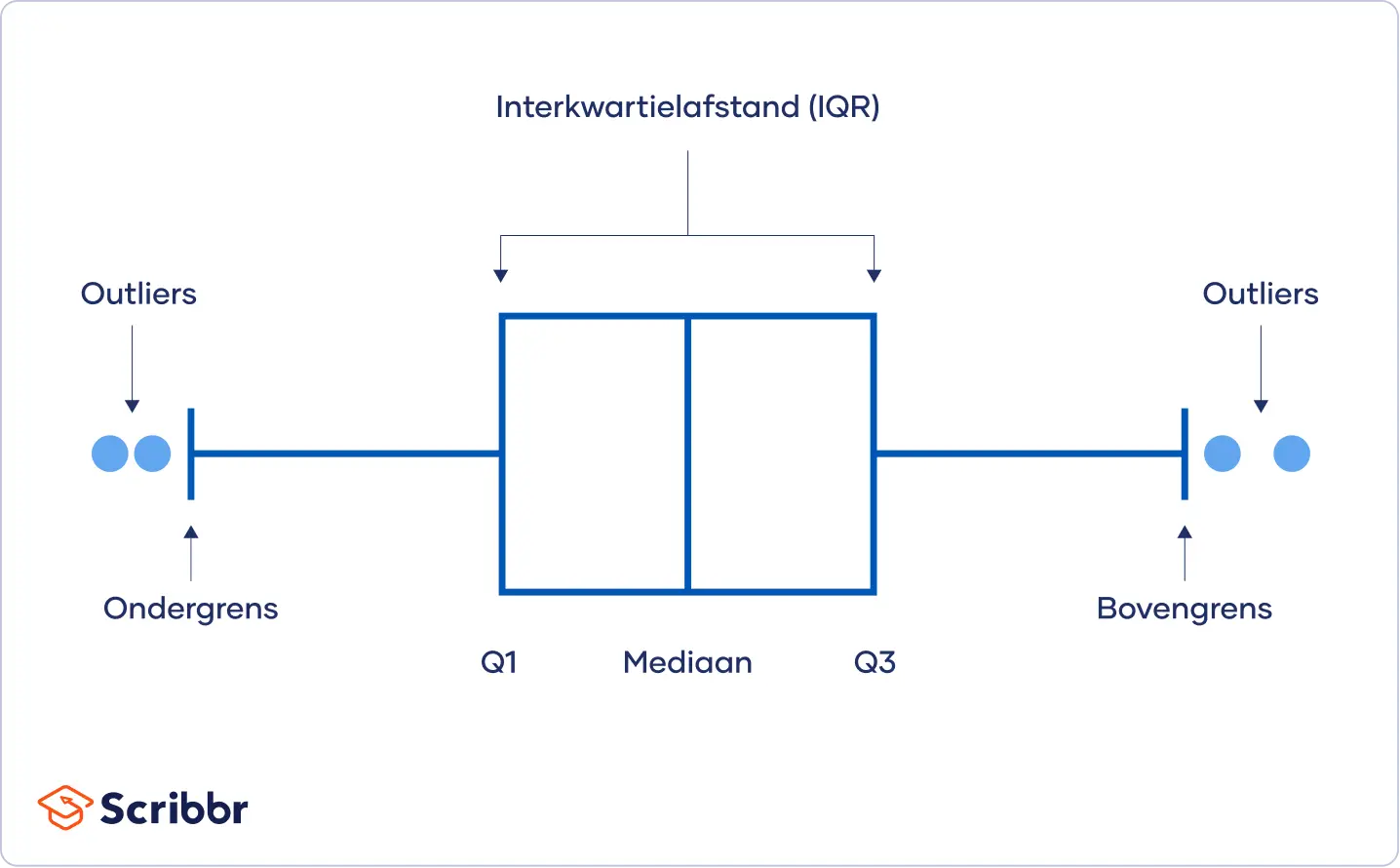
Een boxplot is een visualisatie van vijf belangrijke beschrijvende statistieken, namelijk het minimum, het eerste kwartiel, de mediaan, het derde kwartiel en het maximum. Soms worden zwakke en sterke uitschieters (outliers) ook opgenomen in een boxplot.

Een boxplot zegt iets over de verdeling van de data. Door naar de breedtes van de “dozen” (boxes) te kijken, kun je zien hoe de data verdeeld zijn over de kwartielen.

Wat is een boxplot?

Een boxplot is een visuele weergave van de vijf statistieken die je gebruikt voor de vijf-getallensamenvatting (five number summary). Dit is een samenvatting van alle kwartielen van een dataset, waarbij het minimum en maximum soms als Q0 (het nulste kwartiel) en Q4 (het vierde kwartiel) worden gezien.

De vijf-getallensamenvatting bestaat uit:

• Minimum (ondergrens): Dit is de laagste waarde in de dataset.
• Eerste kwartiel (Q1): 25% van de waarden bevindt zich onder de grenswaarde van het eerste kwartiel.
• Mediaan (tweede kwartiel, Q2): De middelste waarde in je dataset als je de datapunten rangschikt van klein naar groot.
• Derde kwartiel (Q3): 75% van de waarden bevindt zich onder de grenswaarde van het derde kwartiel.
• Maximum (bovengrens): Dit is de hoogste waarde in de dataset.

Een boxplot is niet alleen handig om de centrale tendens, spreiding en eventuele scheefheid (skewness) in een dataset te visualiseren. Je kunt namelijk ook verschillende boxplots met elkaar vergelijken door te onderzoeken of ze overlappen.

Ontvang feedback op taal, structuur, lay-out en bronvermelding

Professionele Scribbr-editors kijken je scriptie na op:

• Academisch taalgebruik
• Onduidelijke zinnen
• Grammaticale fouten
• Interpunctie
• Verboden woorden

Bekijk het voorbeeld

Hoe maak je een boxplot?

Je kunt zelf een boxplot tekenen, maar het is ook mogelijk om deze automatisch te laten maken in Excel, R of SPSS. In het onderstaande voorbeeld wordt een horizontale boxplot handmatig getekend.

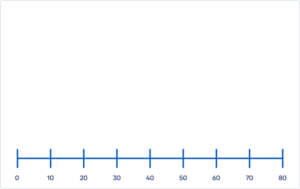
Stap 1: Teken en label de as

Teken een x-as of y-as en geef met streepjes ankerpunten aan. Zorg ervoor dat de intervallen steeds gelijk zijn (in het voorbeeld is ieder interval gelijk aan 10).

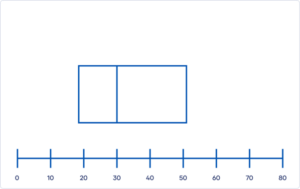
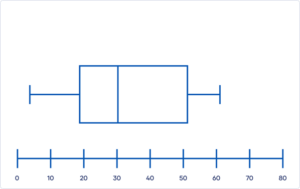
Stap 2: Teken de box

Teken nu een box van de ondergrens van het eerste kwartiel (Q1) naar de bovengrens van het derde kwartiel (Q3). De hoogte van de box is niet van belang.

Je deelt de box in tweeën door een verticale streep ter hoogte van de mediaan te zetten. In het voorbeeld is Q1 gelijk aan 18, de mediaan aan 30, en Q3 aan 52.

Stap 3: Teken de whiskers

Teken vervolgens de whiskers tot de minimumwaarde (links) en de maximumwaarde (rechts). In het voorbeeld is de minimumwaarde 3 en de maximumwaarde 62.

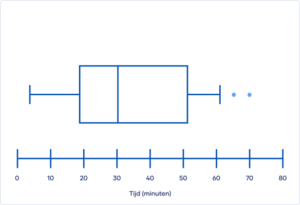
Stap 4 (optioneel): Neem de outliers op in de boxplot

Eventueel kun je outliers opnemen in je boxplot. Deze geef je vaak aan met een stip of een asterisk (*). Ook kun je de as een naam geven. In het voorbeeld zijn er twee outliers (65 en 70) en geeft de x-as de tijd in minuten weer.

Hoe lees je een boxplot af?

Een boxplot geeft veel informatie over de spreiding in een dataset. Je kunt de volgende statistieken aflezen of berekenen op basis van een boxplot:

• Minimum
• Eerste kwartiel
• Mediaan
• Derde kwartiel
• Maximum
• Spreidingsbreedte (bereik, range; maximum – minimum)
• Interkwartielafstand (interquartile range; Q3 – Q1)

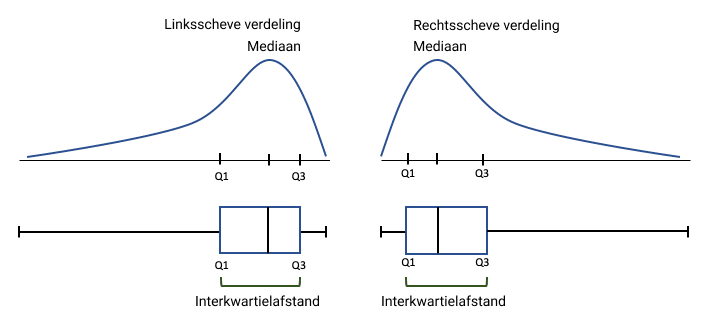
Een smalle box wijst op minder spreiding, terwijl een bredere box op meer spreiding wijst. Ook kan de plaatsing van de box iets zeggen over de scheefheid van de verdeling.

• Een box die dichter bij de rechter whisker staat wijst op een linksscheve (negatiefscheve) verdeling.
• Een box die dichter bij de linker whisker staat wijst op een rechtsscheve (positiefscheve) verdeling.

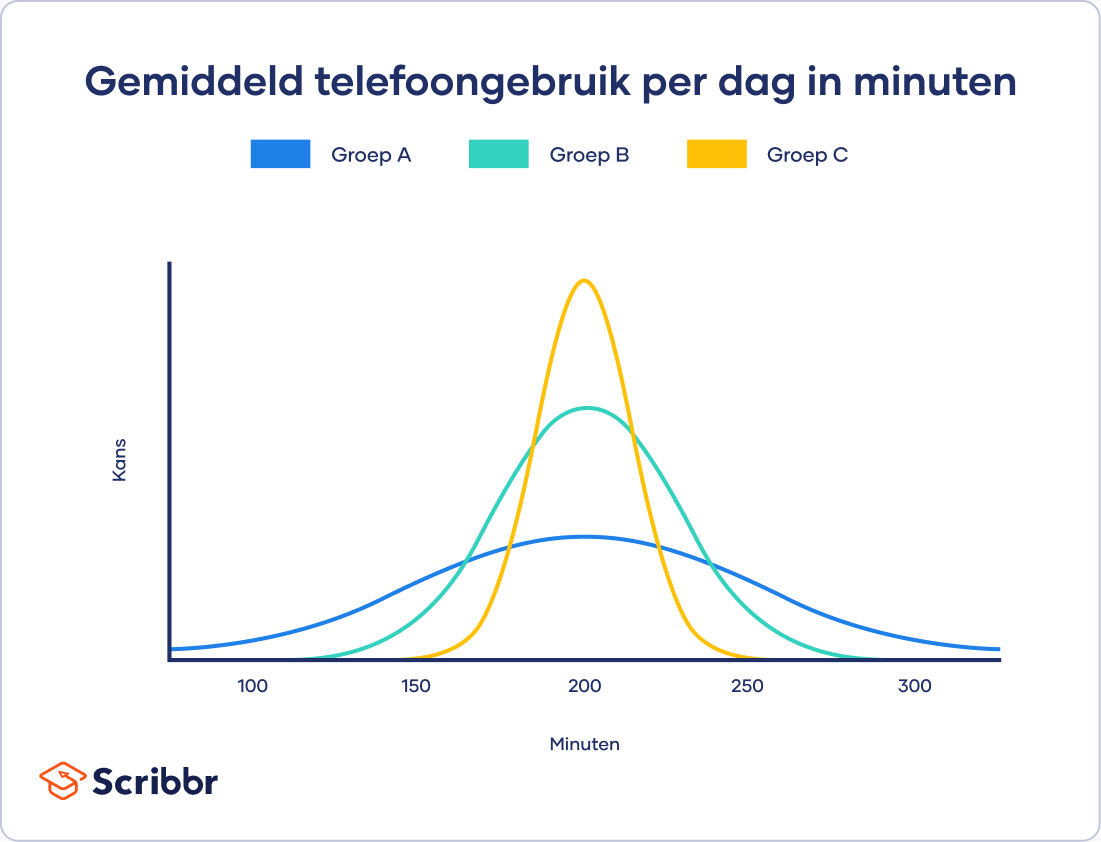
Voorbeeld: Boxplot van gemiddeld telefoongebruik per dag

De volgende boxplots laten het gemiddelde telefoongebruik per dag in minuten zien voor drie groepen (Groep A, Groep B en Groep C).

De vijf-getallensamenvatting kan worden opgesteld door de waarden op de y-as af te lezen ter hoogte van de whiskers en horizontale lijnen.

Hoewel de mediaan (middelste waarde in de dataset) overal hetzelfde is, verschilt de spreiding sterk. Zo is de afstand tussen de minimale en maximale waarde (het bereik) veel groter bij Groep A dan bij Groep B en Groep C. Ook is de box zelf breder bij Groep A, wat wijst op meer spreiding dan de smallere boxjes van Groep B en C.

Voor alle groepen geldt dat de boxplot geen scheefheid laat zien en dat de data normaal verdeeld zijn. De box zit namelijk ongeveer in het midden van beide whiskers.

Boxplot versus histogram

Een histogram zegt net als een boxplot iets over de de frequentieverdeling van een dataset. In dat geval zijn de waarden echter gegroepeerd in klassen (bijvoorbeeld 1–5, 5–10, 10–15).

De vorm van een boxplot hangt samen met de vorm van een histogram:

• Als de box van een boxplot smal is, is het histogram op die plek hoog.
• Als de box van een boxplot breed is, is het histogram op die plek laag.

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

Veelgestelde vragen

Hoe maak je een boxplot in R?

Je kunt een boxplot in R maken met de boxplot( )-functie.

Het is het mogelijk om de parameters van de boxplot aan te passen. Zo kun je bijvoorbeeld een titel (main-), labels (xlab en ylab) en de kleur (col) aanpassen. Ook kun je de plotrichting van verticaal naar horizontaal veranderen met het argument horizontal = true.

Hoe maak je een boxplot in Excel?

Tegenwoordig is het eenvoudig om een boxplot in Excel te maken:

1. Selecteer je data
2. Klik op het tabblad “Invoegen”
3. Selecteer “Illustraties”, “Grafiek, en kies voor “Box-and-whisker”

Vervolgens kun je het uiterlijk van de boxplot aanpassen. Zo kun je de volgende dingen tonen:

• Afzonderlijke datapunten
• Outliers
• Gemiddelde
• Labels voor minimum, eerste kwartiel (Q1), mediaan (Q2), derde kwartiel (Q3) en maximum.

Wie heeft de boxplot bedacht?

De boxplot is in 1977 bedacht door de Amerikaanse statisticus John Tukey. De boxplot is een visuele weergave van vijf belangrijke beschrijvende statistieken:

• Minimum
• Eerste kwartiel
• Mediaan
• Derde kwartiel
• Maximum