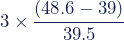Skewness (Scheefheid) | Definities & Voorbeelden
Skewness (scheefheid) is een maat voor de asymmetrie van een verdeling. Een verdeling is asymmetrisch als de linker- en rechterkant geen spiegelbeelden van elkaar zijn.
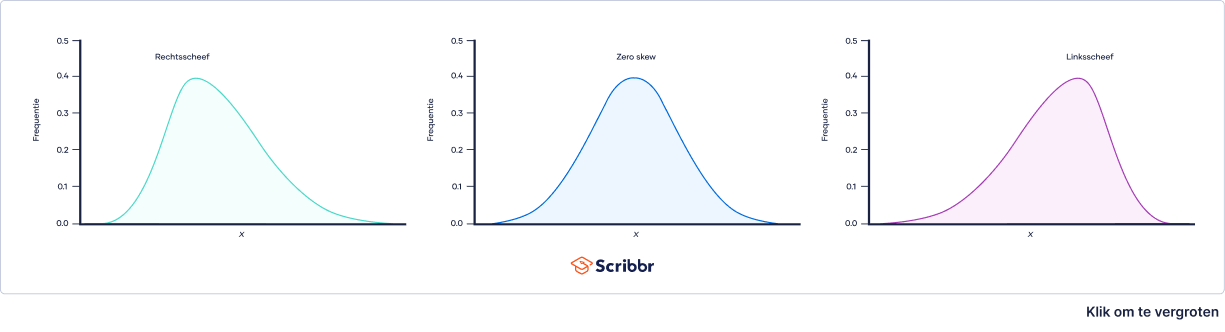
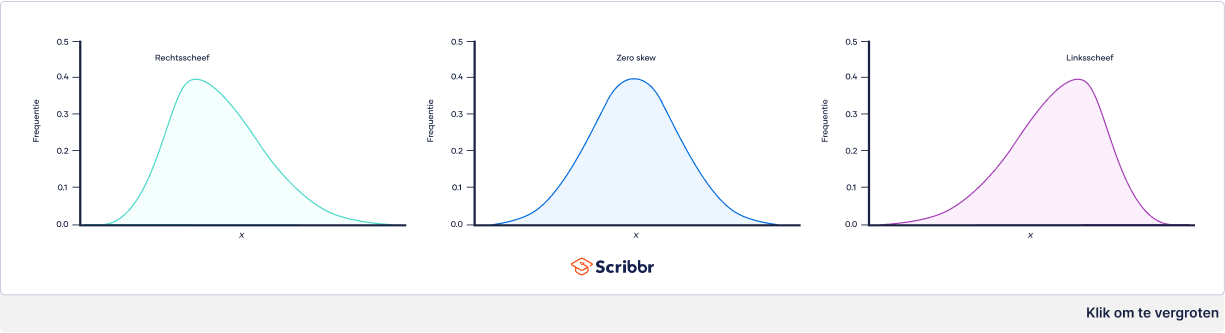
Een verdeling kan rechtse (positieve), linkse (negatieve) of nul scheefheid hebben. Dit wordt ook wel aangeduid als right skew, left skew en zero skew. Een rechtsscheve verdeling is langer aan de rechterkant van de piek en een linksscheve verdeling is langer aan de linkerkant van de piek:
Je kunt de skewness van een verdeling berekenen om:
- De verdeling van een variabele te beschrijven naast andere descriptieve statistieken.
- Te bepalen of een variabele normaal verdeeld is. Een normale verdeling heeft zero skew, wat een voorwaarde is voor veel statistische toetsen.
Wat is zero skew?
Als een verdeling zero skew (nul scheefheid) heeft, is deze symmetrisch. De linker- en rechterkant zijn spiegelbeelden.
Een normale verdeling heeft zero skew, maar deze verdeling is niet de enige met zero skew. Alle symmetrische verdelingen, zoals een uniforme verdeling of sommige bimodale (two-peak) verdelingen, hebben nul scheefheid.
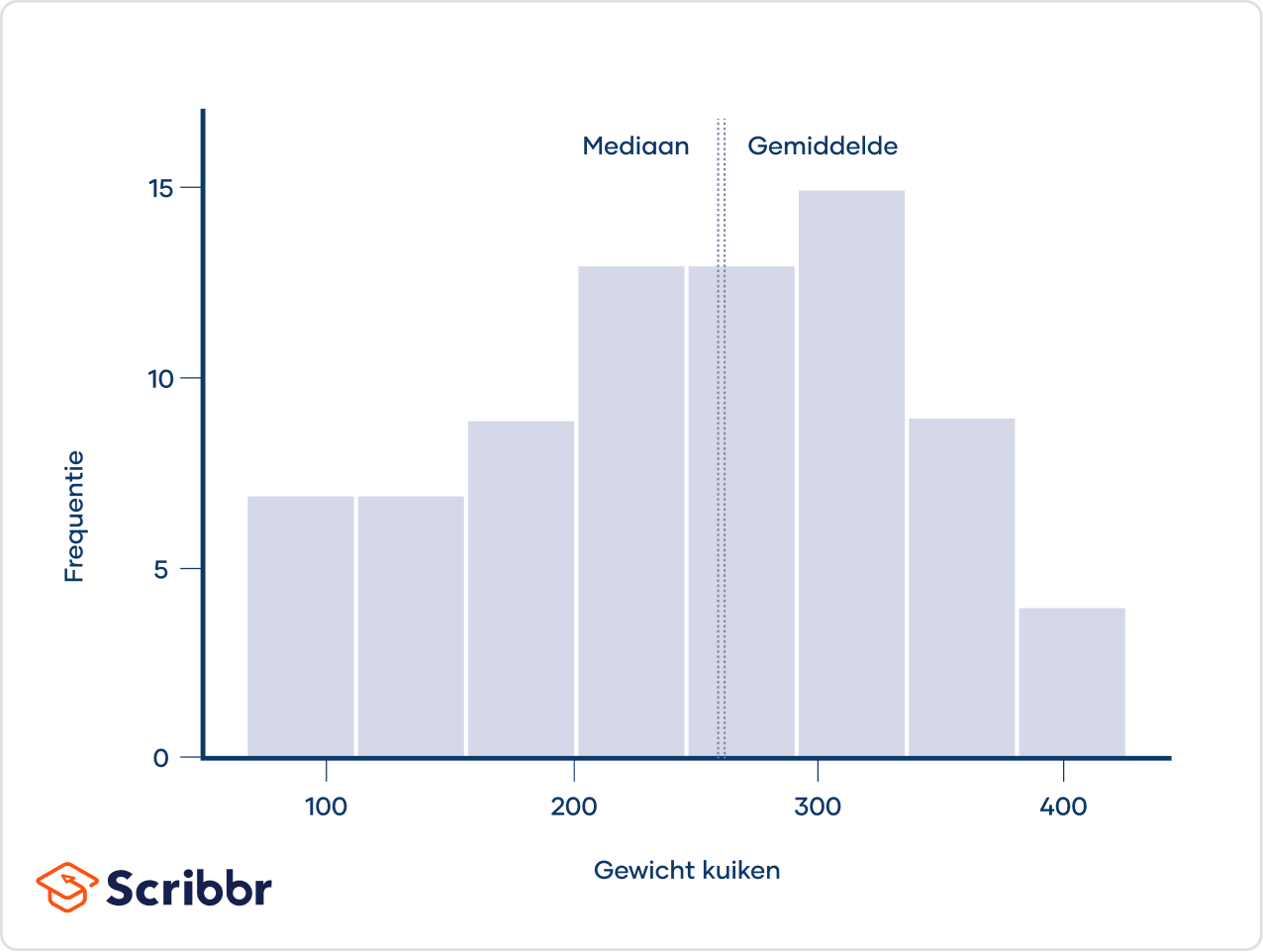
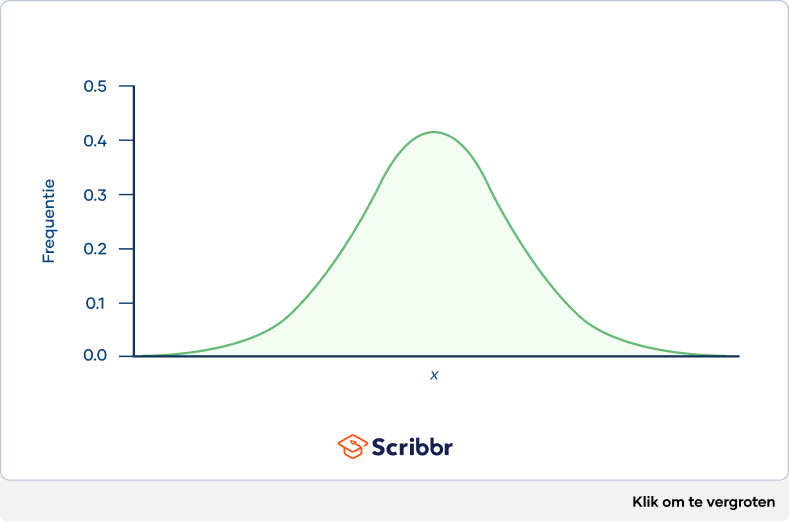
De eenvoudigste manier om na te gaan of een verdeling zero skew heeft, is door de verdeling uit te zetten in een histogram. Ter illustratie zijn hieronder de gewichten van zes weken oude kuikens gevisualiseerd in een histogram.
De verdeling is ongeveer symmetrisch, met de waarnemingen evenredig verdeeld aan de linker- en rechterkant van de piek. De verdeling heeft dus ongeveer zero skew.
In een verdeling met zero skew zijn het gemiddelde en de mediaan ongeveer gelijk.
In het histogram hierboven is het gemiddelde gewicht van de kuikens 261.3 gram en de mediaan 258 gram. Het gemiddelde en de mediaan zijn net niet helemaal gelijk, omdat verdeling van de steekproef een hele kleine scheefheid heeft.
Hoewel een theoretische verdeling (e.g., de z-verdeling) een scheefheid van 0 kan hebben, heeft een echte dataset bijna altijd enige mate van scheefheid. Als een verdeling echter bijna symmetrisch is, kun je alsnog zeggen dat de verdeling zero skew heeft voor praktische doeleinden, zoals het verifiëren van modelaannames.
Lees waarom zo veel studenten Scribbr inschakelen
Wat is right skew (positieve skew)?
Een rechtsscheve verdeling (right-skewed distribution) is langer aan de rechterkant van de piek dan aan de linkerkant. Rechtse scheefheid (right skew) wordt ook wel positieve scheefheid (positive skew) genoemd.
Je kunt skewness begrijpen aan de hand van staarten. Een staart (tail) is een lang, taps toelopend einde van een verdeling. Een staart geeft aan dat er waarnemingen zijn aan één van de uiterste uiteinden van de verdeling, maar dat deze relatief weinig voorkomen. Een rechtsscheve verdeling heeft een lange staart aan de rechterkant.
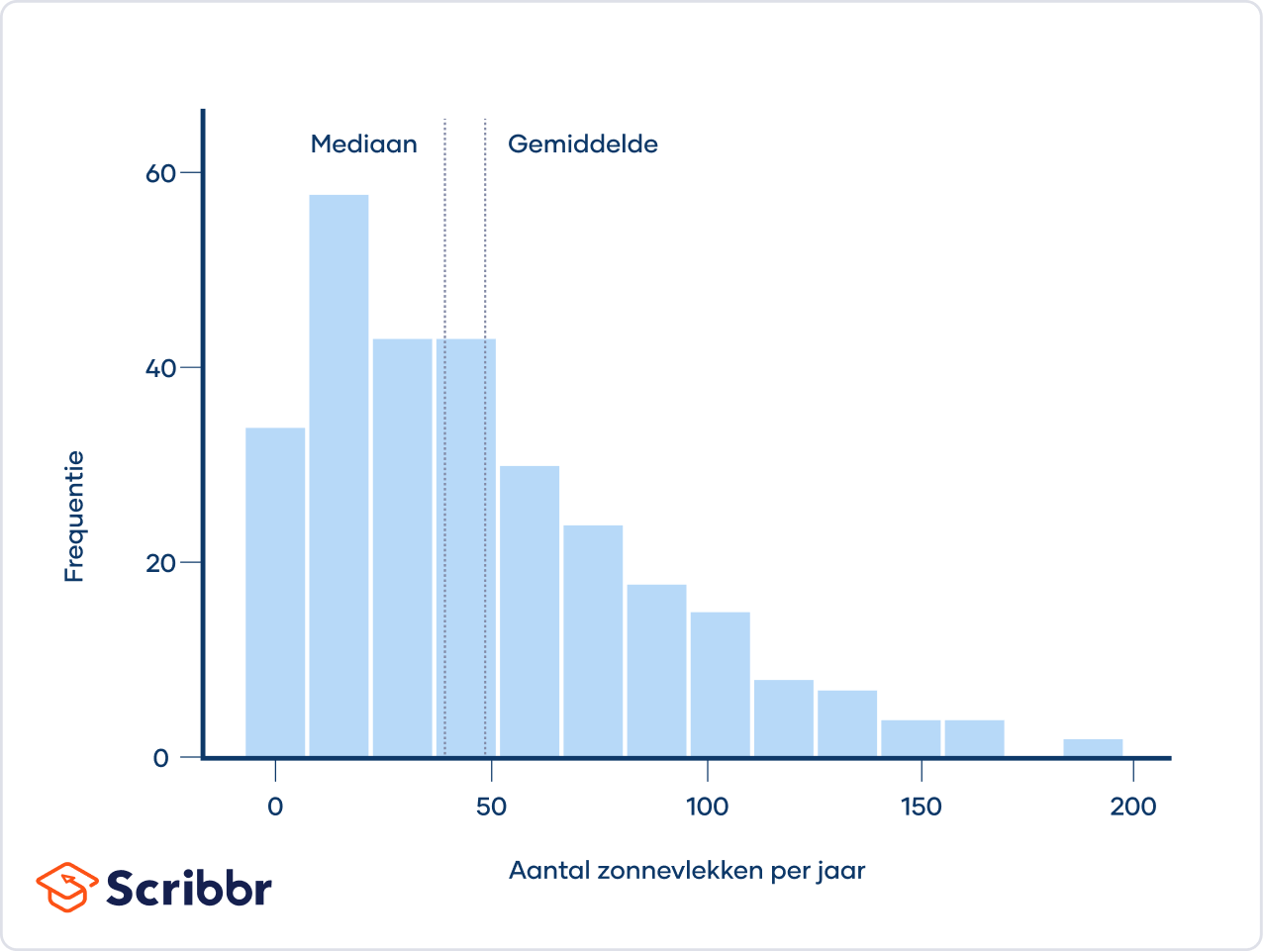
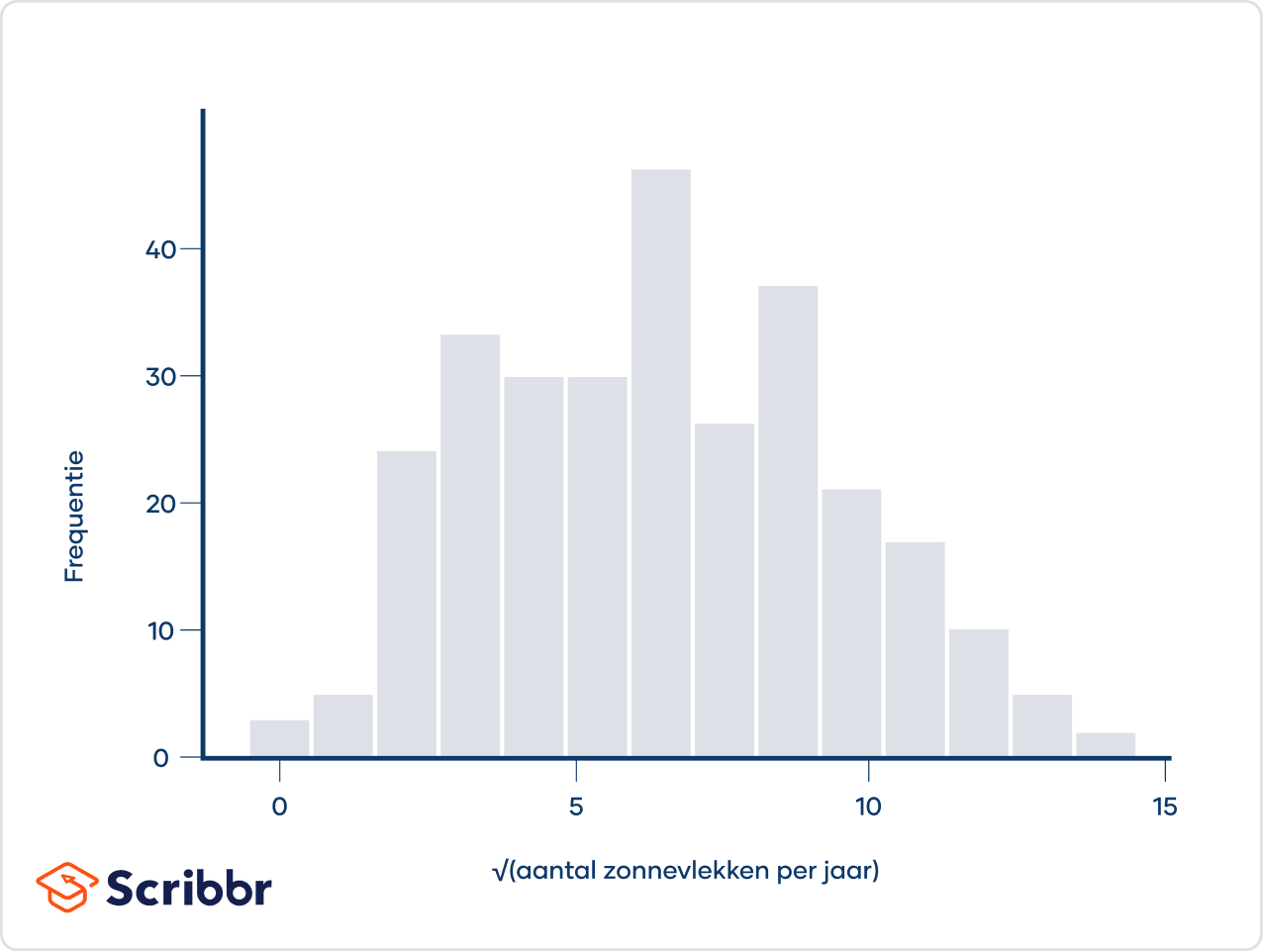
Onderstaand histogram geeft het aantal zonnevlekken dat per jaar wordt waargenomen weer. Dit is een voorbeeld van een rechtsscheve verdeling. De zonnevlekken (i.e., de donkere, koelere gebieden op het zonsoppervlak) zijn tussen 1749 en 1983 door astronomen waargenomen.
De verdeling is rechtsscheef, omdat deze langer is aan de rechterkant van de piek. Er is een lange staart aan de rechterkant, wat betekent dat er om de paar decennia een jaar is waarin het aantal waargenomen zonnevlekken veel hoger is dan gemiddeld.
Het gemiddelde van een rechtsscheve verdeling is bijna altijd hoger dan de mediaan. Dat komt doordat de extreme waarden (de waarden in de staart) meer invloed hebben op het gemiddelde dan op de mediaan.
Het gemiddeld aantal waargenomen zonnevlekken per jaar is bijvoorbeeld 48.6, wat meer is dan de mediaan van 39.
Wat is left skew (negatieve skew)?
Een linksscheve verdeling (left-skewed distribution) is langer aan de linkerkant van de piek dan aan de rechterkant. Met andere woorden: een linksscheve verdeling heeft een lange staart aan de linkerkant. Linkse scheefheid (left skew) wordt ook wel negatieve scheefheid (negative skew) genoemd.
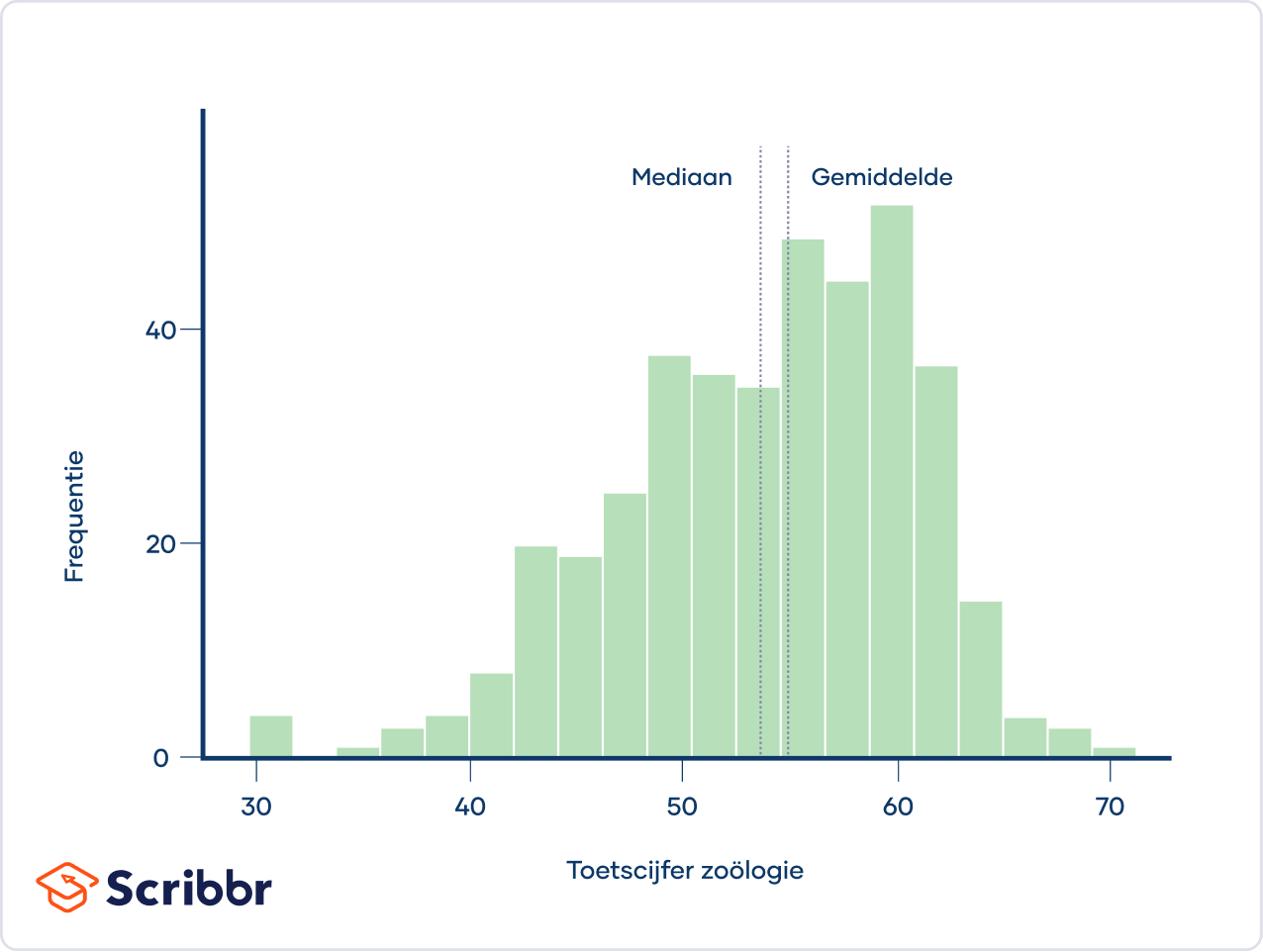
Toetscijfers volgen vaak een linksscheve verdeling, waarbij de meeste leerlingen relatief goed presteren en een paar leerlingen ver onder het gemiddelde presteren. Onderstaand histogram toont de cijfers voor het zoölogie-gedeelte van een gestandaardiseerde toets die Indiase leerlingen aan het eind van de middelbare school moeten afleggen.
De verdeling is linksscheef, omdat deze langer is aan de linkerkant van de piek. De lange staart aan de linkerkant vertegenwoordigt de leerlingen die een heel laag cijfer hebben behaald.
Het gemiddelde van een linksscheve verdeling is bijna altijd lager dan de mediaan.
Het gemiddelde zoölogie-toetscijfer is bijvoorbeeld 53.7, wat lager is dan de mediaan van 55.
Hoe bereken je skewness (scheefheid)?
Er zijn verschillende formules om scheefheid te meten. Eén van de makkelijkste berekeningen is Pearson’s median skewness (Pearsons scheefheid van de mediaan). Deze formule maakt gebruik van het feit dat het gemiddelde en de mediaan ongelijk zijn bij een scheve verdeling.

Pearson’s median skewness geeft het aantal standaarddeviaties aan dat tussen het gemiddelde en de mediaan ligt.
Echte observaties hebben zelden een Pearson’s median skewness van precies 0, maar je mag wel concluderen dat je data zero skew hebben als de waarde dicht bij 0 ligt. Er is geen standaardregel die bepaalt welk getal dicht genoeg bij de 0 ligt voor de data om zero skew te hebben (hoewel dit onderzoek suggereert dat 0.4 en -0.4 redelijke uiterste waarden zijn voor grote steekproeven).
- Gemiddelde: 48.6
- Mediaan: 39
- Standaarddeviatie: 39.5
Berekening
Pearson’s median skewness =
Pearson’s median skewness =
Pearson’s median skewness =
Lees waarom zo veel studenten Scribbr inschakelen
Hoe ga je om met scheve data?
Eén van de redenen om de scheefheid van je data te controleren, is om te bepalen of je data geschikt zijn voor een statistische toets. Veel statistische toetsen vereisen dat data of residuen normaal verdeeld zijn. Skewness (scheefheid) is een veelvoorkomende manier waarop een verdeling kan afwijken van een normale verdeling.
Over het algemeen heb je drie keuzes als je statistische toets een normale verdeling vereist maar je data scheef verdeeld zijn:
- Doe niets. Veel statistische toetsen, waaronder t-toetsen, ANOVA’s en lineaire regressieanalyses, zijn niet erg gevoelig voor scheve data. Vooral als de scheefheid mild of matig is, kun je de skewness soms het beste negeren.
- Gebruik een ander model. Je kunt er ook voor kiezen om een ander model te gebruiken waarbij een normale verdeling geen vereiste is. Niet-parametrische toetsen of gegeneraliseerde lineaire modellen kunnen geschikter zijn voor je data.
- Transformeer de variabele. Een andere optie is het transformeren van de scheve variabele zodat deze minder scheef is. Een variabele transformeren houdt in dat je dezelfde functie toepast op alle waarnemingen van de variabele.
| Soort skew | Intensiteit van skew | Transformatie |
| Rechtsscheef | Mild | Transformeer niet |
| Matig | Vierkantswortel (square root) | |
| Sterk | Natuurlijke logaritme (natural log) | |
| Erg sterk | Logaritme met grondtal 10 (log base 10) | |
| Linksscheef | Mild | Transformeer niet |
| Matig | Reflecteer*, daarna vierkantswortel | |
| Sterk | Reflecteer*, daarna natuurlijke logaritme | |
| Erg sterk | Reflecteer*, daarna logaritme met grondtal 10 |
*In deze context betekent “reflecteer” dat je de grootste waarneming, K, neemt en dan elke waarneming aftrekt van K + 1. Houd er rekening mee dat door spiegeling van de waarden de richting van de variabele en de relaties met andere variabelen omgekeerd wordt (i.e., een positief verband wordt negatief en andersom).
Aangezien het aantal zonnevlekken dat per jaar wordt waargenomen rechtsscheef (right-skewed) verdeeld is, kun je proberen dit probleem op te lossen door de variabele te transformeren. Je kunt er ook voor kiezen om de scheefheid te negeren, aangezien lineaire regressies niet erg gevoelig zijn voor skew.
Voor de datatransformatie begin je met een vierkantswortel-transformatie. Als dat niet voldoende blijkt, kun je verdergaan naar de volgende optie voor transformatie.
| Aantal zonnevlekken per jaar | √(aantal zonnevlekken per jaar) |
| 5 | 2.236 |
| 11 | 3.317 |
| 16 | 4.000 |
| 23 | 4.796 |
| … | … |
Als je de getransformeerde variabele visualiseert in een histogram, zie je dat de scheefheid nu bijna 0 is. Je kunt het aantal zonnevlekken per jaar vervangen door de getransformeerde variabele in de lineaire regressie. Waarschijnlijk zullen de residuen van de lineaire regressie nu normaal verdeeld zijn.
Oefenvragen over skewness
Veelgestelde vragen over skewness (scheefheid)
- Wat is het verschil tussen skewness en kurtosis?
-
Skewness en kurtosis zijn beide belangrijke maten voor de vorm van een verdeling.
- Skewness (scheefheid) meet de asymmetrie van een verdeling.
- Kurtosis (welving) meet de dikte van de staart van een verdeling ten opzichte van de normale verdeling.
- Wat zijn de drie soorten skewness (scheefheid)?
-
De drie soorten skewness (scheefheid) zijn:
- Rechtsscheef (right skew). Een rechtsscheve verdeling (ook wel positief-scheve verdeling genoemd) is langer aan de rechterkant van de piek dan aan de linkerkant.
- Linksscheef (left skew). Een linksscheve verdeling (ook wel negatief-scheve verdeling genoemd) is langer aan de linkerkant van de piek dan aan de rechterkant.
- Zero skew. Een verdeling met zero skew (nul scheefheid) is symmetrisch, wat inhoudt dat de linker- en rechterkant spiegelbeelden van elkaar zijn.
- Wat is een normale verdeling?
-
Er zijn twee parameters die bepalen hoe de normale verdeling eruitziet: het gemiddelde en de standaarddeviatie.
- Binnen één standaarddeviatie ligt 68,2% van de observaties (34,1% + 34,1%), binnen twee standaarddeviaties 95,2% en binnen drie standaarddeviaties 99,6%.
- De centrummaten (gemiddelde, modus en mediaan) hebben bij een normale verdeling dezelfde waarde.
- De data zijn symmetrisch verdeeld, zonder skewness (zero skew).
- Wat is skewness?
-
Skewness is de Engelse term voor scheefheid.
Scheefheid is een maat voor asymmetrie van een verdeling. Een scheve verdeling kan rechtsscheef of linksscheef zijn. Een normale verdeling heeft zero skew.
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Scharwächter, V. (2022, 14 juli). Skewness (Scheefheid) | Definities & Voorbeelden. Scribbr. Geraadpleegd op 9 december 2024, van https://www.scribbr.nl/statistiek/skewness-scheefheid/