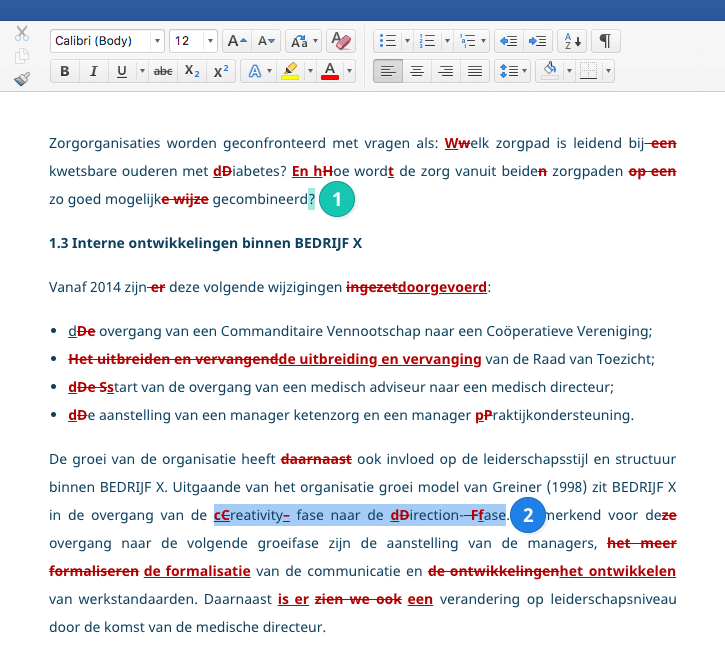
Meetniveaus: nominaal, ordinaal, interval en ratio | Voorbeelden
Meetniveaus, ook wel meetschalen genoemd, zeggen iets over hoe nauwkeurig de variabelen (in een experiment) zijn gemeten. In wetenschappelijk onderzoek worden variabelen gedefinieerd als de elementen uit je dataset die verschillende waarden kunnen aannemen (zoals lengte, moedertaal, of proefwerkcijfers).
Er zijn vier meetniveaus:
- Nominaal: de data kunnen alleen worden gecategoriseerd, zonder duidelijke rangorde.
- Ordinaal: de data kunnen worden gecategoriseerd en er is sprake van een duidelijke rangorde.
- Interval: de data kunnen worden gecategoriseerd, er is sprake van een rangorde en de intervallen tussen de categorieën zijn gelijk (bijvoorbeeld steeds een stap van 10).
- Ratio: de data kunnen worden gecategoriseerd, er is sprake van een rangorde, de intervallen tussen de categorieën zijn gelijk en er is een betekenisvol nulpunt.
De manieren waarop je je data kunt analyseren zijn afhankelijk van het meetniveau van je variabele(n). Hoe lager het meetniveau, hoe minder complex en nauwkeurig de analyse is. Een nominaal meetniveau is het laagst, gevolgd door ordinaal, interval en ten slotte ratio. De meetniveaus interval en ratio worden samen scale genoemd.
Nominaal, ordinaal, interval en ratio data
Een hoger meetniveau heeft alle eigenschappen van de lagere meetniveaus plus een nieuwe eigenschap. Zo heeft het meetniveau ratio dus alle eigenschappen van het nominale, ordinale en intervalniveau met een extra eigenschap: een betekenisvol nulpunt.
| Nominaal niveau | Voorbeelden van nominale schalen |
|---|---|
| Je kunt je data categoriseren door labels toe te kennen. Elk datapunt kan maar tot één label behoren en er is geen rangorde. |
|
| Ordinaal niveau | Voorbeelden van ordinale schalen |
| Je kunt je data categoriseren en rangschikken, maar je kunt niets zeggen over de intervallen tussen de categorieën. De intervallen zijn niet te bepalen of niet betekenisvol.
Zo kun je bijvoorbeeld een top vijf van Olympische medaillewinnaars opstellen, maar dat zegt niet dat tussen iedere winnaar evenveel verschil zit in termen van gewonnen wedstrijden. Wellicht heeft de nummer 1 twee wedstrijden meer gewonnen dan de nummer 2, maar heeft de nummer 2 vier wedstrijden meer gewonnen dan de nummer 3. |
|
| Intervalniveau | Voorbeelden van intervalschalen |
| Je kunt de data categoriseren en rangschikken, en er zijn gelijke intervallen tussen de categorieën. Er is geen betekenisvol of absoluut nulpunt.
Het verschil tussen twee opeenvolgende temperaturen is hetzelfde: 1 graad. Je kunt dus spreken van gelijke intervallen. Nul graden betekent echter niet hetzelfde op alle temperatuurschalen: het betekent meestal niet dat er geen temperatuur is. Dit geldt bijvoorbeeld ook voor testscores: als iemand een 0 haalt op een toets betekent dat niet dat diegene helemaal niet over de gemeten vaardigheid beschikt. Het nulpunt bij een toets is dus arbitrair. |
|
| Rationiveau | Voorbeelden van ratioschalen |
| Je kunt je data categoriseren en rangschikken, en er is sprake van gelijke intervallen tussen opeenvolgende datapunten. Ook is er een betekenisvol of absoluut nulpunt.
Een betekenisvol nulpunt betekent dat de bestudeerde variabele bij 0 helemaal afwezig is. Bij ratioschalen staat 0 dus gelijk aan die absolute afwezigheid van de eigenschap. Een voorbeeld hiervan is de temperatuur in Kelvin. Hierbij heb je geen negatieve temperatuurwaarden (zoals een temperatuur van -3). In dit geval betekent 0 dus daadwerkelijk dat er geen thermische energie aanwezig is. |
|
Lees waarom zo veel studenten Scribbr inschakelen
Waarom zijn meetniveaus belangrijk?
Het meetniveau van een variabele bepaalt op welke manier(en) je je data kunt analyseren.
De verschillende niveaus bepalen ook welke descriptieve statistieken je kunt gebruiken om je data samen te vatten en welke soorten inferentiële statistiek (ook wel toetsende of verklarende statistiek genoemd) je kunt gebruiken om je hypothese te ondersteunen of te weerleggen.
Vaak kunnen je variabelen op meerdere niveaus worden gemeten en in die gevallen moet je zelf beslissen welk meetniveau je wilt gebruiken. Die beslissing neem je dan ook voorafgaand aan je dataverzameling.
- Ordinaal niveau: Je creëert inkomenscategorieën met een oplopend bereik, bijvoorbeeld: €0 – €19.999, €20.000 – €39.999, en €40.000 – €59.999. Je vraagt participanten om de categorie te kiezen waarbinnen hun jaarinkomen valt. Je codeert de categorieën bijvoorbeeld met nummers 1 tot en met 3 voor de statistische analyse.
- Rationiveau: Je verzamelt data door participanten te vragen wat hun exacte jaarinkomen is.
| Participant | Inkomen (ordinaal niveau) | Inkomen (rationiveau) |
|---|---|---|
| A | Categorie 1 | €12.550,- |
| B | Categorie 2 | €39.700.- |
| C | Categorie 3 | €40.300.- |
Op rationiveau kun je zien dat het verschil tussen inkomen A en B veel groter is dan dat tussen inkomen B en C. Je kunt individuele participanten rangschikken.
Op ordinaal niveau weet je echter alleen binnen welke categorie een inkomen valt en niet het precieze inkomen. Aangezien je niet weet hoeveel ieder inkomen verschilt van de andere inkomens in de dataset, kun je de participanten alleen groeperen en die groepen rangschikken van laag naar hoog.
Welke descriptieve statistieken kan ik toepassen op mijn data?
Descriptieve statistiek helpt je om een idee te krijgen van de gemiddelden voor variabelen en van de spreiding van de data. Hiervoor gebruik je centrummaten en spreidingsmaten.
Als je de centrale tendens of variatie probeert te onderzoeken, bepaalt het meetniveau welke methoden je hiervoor kunt gebruiken. Ook hier geldt weer dat alle methoden die geschikt zijn voor de lagere niveaus gebruikt kunnen worden voor de hogere niveaus.
| Datasoort | Wiskundige berekeningen | Centrummaten | Spreidingsmaten |
|---|---|---|---|
| Nominaal |
|
|
|
| Ordinaal |
|
|
|
| Interval |
|
||
| Ratio |
|
|
|
Voorbeelden: Nominaal, ordinaal, interval of ratio?
- De verschillende geboorteplaatsen vormen aparte categorieën (bijvoorbeeld Nijmegen, Utrecht en Horssen).
- Iedere participant kan maar tot één categorie behoren.
- De categorieën kunnen niet gerangschikt worden (de ene plaats komt niet hoger te staan dan een andere plaats).
Het gaat dus om nominale data.
- Iedere participant kan maar tot één categorie behoren.
- De categorieën kunnen worden gerangschikt (van heel weinig plezier tot heel veel plezier).
- Er kan niet worden vastgesteld of de intervallen gelijk zijn.
Het gaat dus om ordinale data.
- De data kan worden gecategoriseerd, gerangschikt en de intervallen zijn gelijk.
- Het nulpunt is geen absoluut nulpunt, omdat de score 0 alsnog wijst op de aanwezigheid van angstgevoelens.
Het gaat hier dus om intervaldata.
- Het aantal uur kan worden gecategoriseerd, gerangschikt en de intervallen zijn gelijk.
- Het nulpunt (0 uur) is betekenisvol.
Het gaat dus om ratiodata.
Veelgestelde vragen
- Wat zijn de vier meetniveaus?
-
Meetniveaus laten zien hoe precies variabelen worden gemeten. Er zijn vier meetniveaus (of meetschalen) die van laag naar hoog kunnen worden gerangschikt.
- Nominaal: De data kunnen alleen worden gecategoriseerd (geen rangorde).
- Ordinaal: De data kunnen worden gecategoriseerd en gerangschikt.
- Interval: De data kunnen worden gecategoriseerd en gerangschikt en er zijn gelijke intervallen tussen de categorieën.
- Ratio: De data kunnen worden gecategoriseerd en gerangschikt, de intervallen zijn gelijk, en er is een absoluut of betekenisvol nulpunt.
- Waarom zijn meetniveaus van belang?
-
Het niveau waarop je een variabele meet, bepaalt hoe je je data kunt analyseren.
Afhankelijk van het meetniveau kun je diverse descriptieve statistieken gebruiken om je data samen te vatten. Ook kun je inferentiële statistiek (ook wel toetsende of verklarende statistiek genoemd) gebruiken om te bepalen of je resultaten de hypothese ondersteunen of weerleggen.
- Hoe bepaal ik welk meetniveau ik moet gebruiken?
-
Sommige variabelen gaan gepaard met een vaststaand meetniveau. Zo worden gender of etniciteit altijd op nominaal niveau gemeten, omdat je de categorieën niet kunt rangschikken.
Bij andere variabelen kun je het meetniveau wel kiezen. De variabele “studenteninkomen” kan bijvoorbeeld op ordinaal of rationiveau worden gemeten.
- Op ordinaal niveau zou je vijf groepen kunnen creëren met een bepaald bereik (bijvoorbeeld 0 – 499, 500 – 799, 800 – 1099, 1100 – 1999 en 2000 – 2299). Participanten kruisen dan het juiste bereik aan.
- Op rationiveau zou je naar het exacte inkomen vragen.
Als je kunt kiezen, is het beter om op rationiveau te meten, zodat je de data op meer manieren kunt analyseren. Hoe hoger je meetniveau, hoe preciezer de data.
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Merkus, J. (2021, 07 juli). Meetniveaus: nominaal, ordinaal, interval en ratio | Voorbeelden. Scribbr. Geraadpleegd op 18 november 2024, van https://www.scribbr.nl/statistiek/meetniveaus/
