Spreidingsmaten: Bereik, standaarddeviatie, variantie en meer
De spreiding geeft aan hoe ver datapunten van elkaar en van het centrum van een verdeling verwijderd zijn. Je gebruikt spreidingsmaten in combinatie met centrummaten om de data samen te vatten met beschrijvende statistieken.
Spreiding wordt ook wel variabiliteit genoemd. Meestal gebruik je een van de volgende spreidingsmaten (measures of variability):
- Bereik (range): het verschil tussen de hoogste en laagste waarde.
- Interkwartielafstand (interquartile range): het verschil tussen het eerste en derde kwartiel.
- Standaarddeviatie (standard deviation): de gemiddelde afstand tot het gemiddelde.
- Variantie (variance): het rekenkundig gemiddelde van de kwadratische afwijkingen van het gemiddelde.
Waarom is spreiding van belang?
De centrale tendens vertelt je waar de meeste datapunten liggen, terwijl de spreiding iets zegt over hoe ver de datapunten uit elkaar liggen. Dit is belangrijk, omdat je bij veel spreiding of variatie moet oppassen met interpreteren en generaliseren.
Weinig spreiding of lage variabiliteit is ideaal, omdat dit betekent dat je betere voorspellingen kunt doen over de populatie op basis van steekproefdata. Veel spreiding of hoge variabiliteit betekent dat de waarden minder consistent zijn, dus het is moeilijker om voorspellingen te doen over de populatie.
Datasets kunnen dezelfde centrale tendens hebben, maar een verschillende mate van spreiding (of andersom). Je kunt dus niets zeggen over de spreiding op basis van de centrummaten, en je kunt ook niets zeggen over de centrummaten op basis van spreidingsmaten. Je hebt beide soorten nodig om een volledig beeld te krijgen van je data.
Met behulp van enkelvoudige, aselecte steekproeven verzamel je gegevens voor drie groepen:
Groep A: middelbare scholieren
Groep B: studenten
Groep C: volwassen, fulltime werknemers
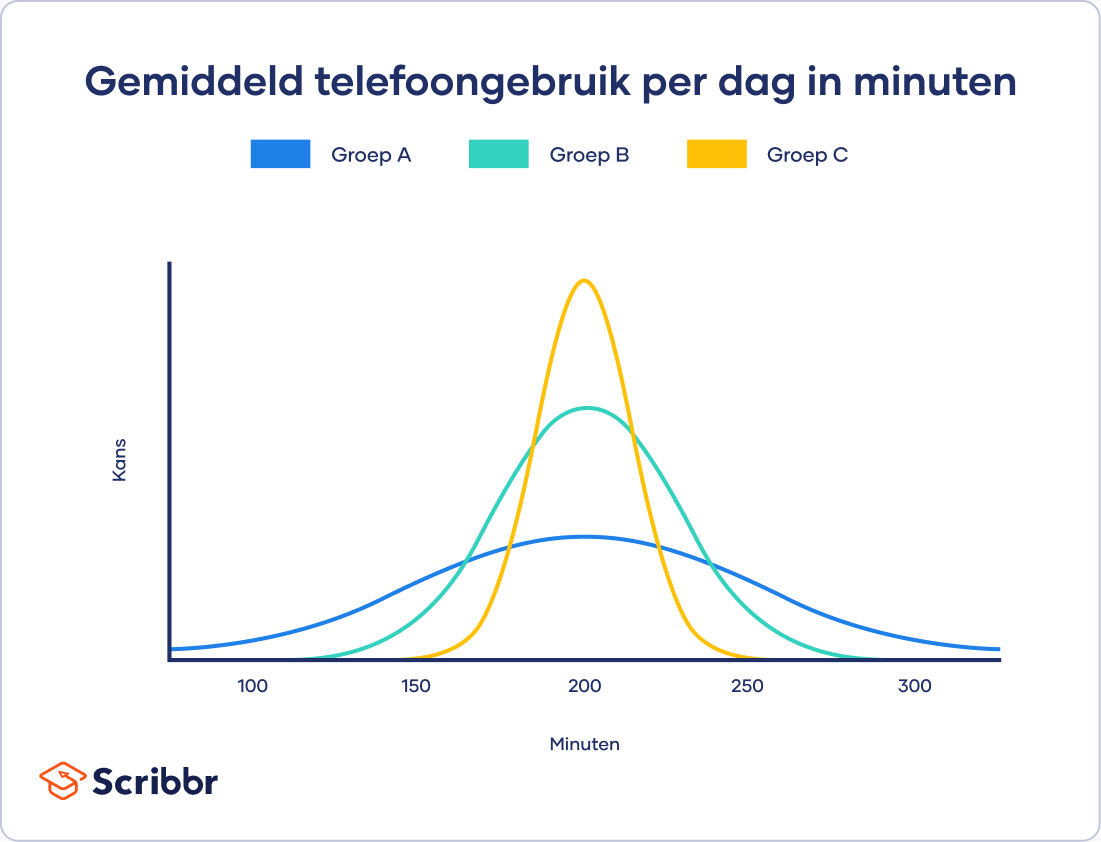
Alle drie de groepen gebruiken hun telefoon gemiddeld even lang (namelijk 195 minuten). Deze waarde zie je op de x-as, bij de pieken voor iedere curve.
Hoewel de data normaal verdeeld zijn, is de spreiding voor iedere groep anders. Groep A vertoont de meeste spreiding, terwijl groep C de minste spreiding laat zien.
Bereik (range)
Het bereik zegt iets over de spreiding van je data tussen de laagste en de hoogste waarde in je dataset. Deze maat is het makkelijkst te berekenen.
Je kunt het bereik bepalen door de laagste waarde van de hoogste waarde af te trekken.
| Data (minuten) | 72 | 110 | 134 | 190 | 238 | 287 | 305 | 324 |
|---|
De hoogste waarde (H) is 324 en de laagste (L) is 72. Je berekent het bereik (R of B) als volgt:
R = H – L
R = 324 – 72 = 252
Het bereik van je dataset is 252 minuten.
Aangezien je slechts 2 waarden gebruikt om het bereik te berekenen, wordt deze maat sterk beïnvloed door uitbijters (outliers) en geeft het bereik geen informatie over de verdeling. Daarom kun je deze maat het beste alleen gebruiken in combinatie met andere maten.
Interkwartielafstand (interquartile range)
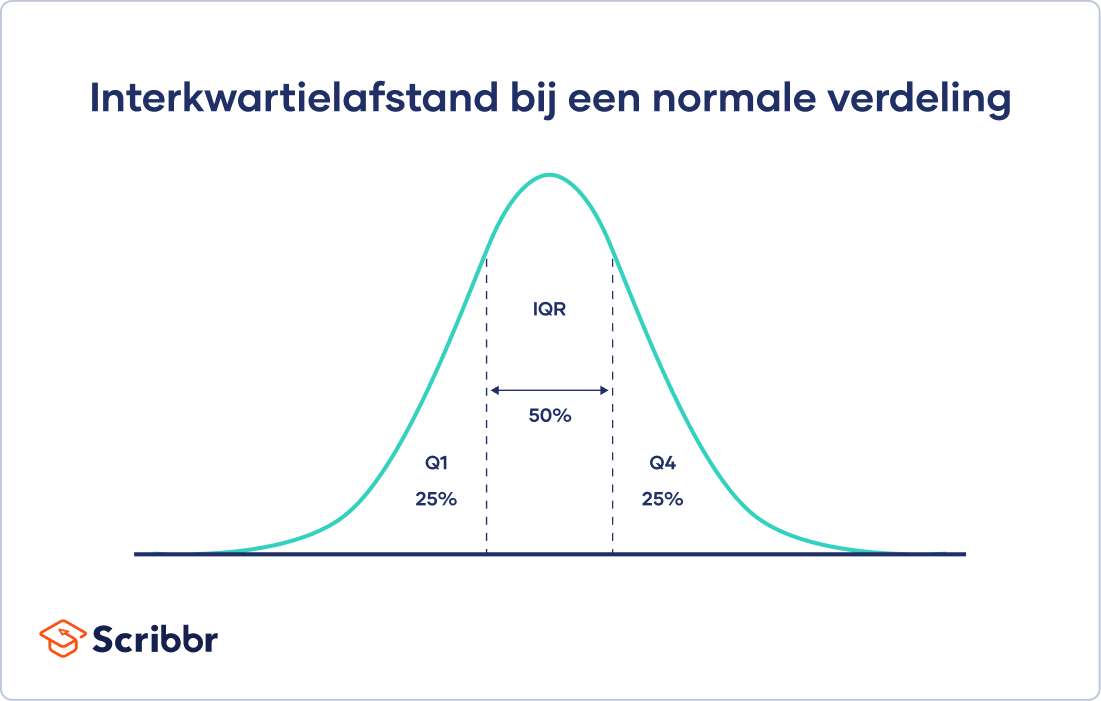
De interkwartielafstand geeft informatie over het interval tussen het eerste en derde kwartiel van je verdeling (de “middelste helft”).
Voor iedere verdeling die van laag naar hoog is gerangschikt, bevat de interkwartielafstand (IQR) de helft van de waarden.
Je berekent de interkwartielafstand door de waarde voor het eerste kwartiel (Q1) af te trekken van de waarde voor het derde kwartiel (Q3). Dit geeft je het bereik van de middelste helft van de dataset.
Vermenigvuldig het aantal waarden in de dataset (8) met 0,25 om het 25e percentiel (Q1) te bepalen en vermenigvuldig het aantal waarden met 0,75 om het 75e percentiel (Q3) te bepalen.
Q1-positie: 0,25 * 8 = 2
Q3-positie: 0,75 * 8 = 6
Q1 is de waarde op de 2de positie, dus in dit geval 110. Q3 is de waarde op de 6de positie, dus in dit geval 287.
IQR = Q3 – Q1
IQR = 287 – 110 = 177
De interkwartielafstand van je dataset is 177 minuten.
Je gebruikt voor de interkwartielafstand slechts 2 waarden, net als voor het bereik. Toch is de interkwartielafstand minder gevoelig voor uitbijters, omdat je in dit geval gebruikmaakt van waarden uit het midden van de dataset. De kans dat dit extreme waarden zijn, is dus veel kleiner, want uitbijters bevinden zich aan de uiteinden van de dataset.
De interkwartielafstand is een goede spreidingsmaat voor zowel scheve als normale verdelingen.
Verdeling samenvatten met vijf waarden
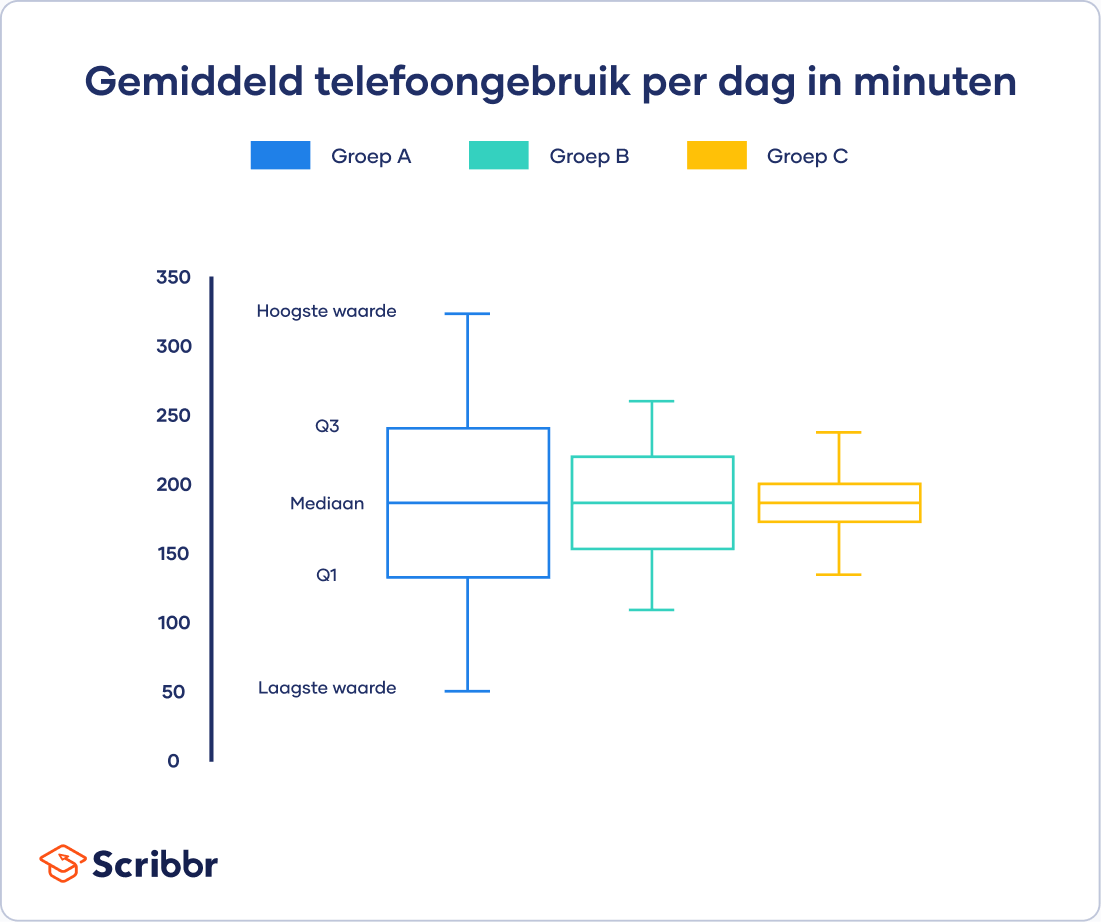
Je kunt iedere verdeling samenvatten door vijf waarden te gebruiken (five-number summary):
- Laagste waarde
- Q1: 25e percentiel
- Q2: de mediaan
- Q3: 75e percentiel
- Hoogste waarde
Je kunt deze “samenvattingen” visualiseren met een boxplot of whisker plot.
Standaarddeviatie of standaardafwijking
De standaarddeviatie of standaardafwijking (standard deviation) is de gemiddelde hoeveelheid spreiding in je dataset.
Deze maat vertelt je hoe ver iedere score gemiddeld genomen verwijderd is van het centrum van de verdeling (het gemiddelde). Des te groter de standaarddeviatie, des te meer spreiding er is.
Je kunt de standaarddeviatie handmatig berekenen met de volgende zes stappen (al kunnen programma’s als Excel en SPSS deze automatisch berekenen):
- Maak een overzicht van alle waarden en bepaal het gemiddelde.
- Bepaal de afstand tot het gemiddelde door het gemiddelde af te trekken van iedere waarde.
- Kwadrateer al deze afwijkingen van het gemiddelde.
- Tel alle gekwadrateerde afwijkingen bij elkaar op.
- Deel de som van de gekwadrateerde afwijkingen door n – 1 (voor een steekproef) of N (voor een populatie).
- Bepaal de wortel van de uitkomst bij Stap 5.
| Stap 1: Data (minuten) | Stap 2: Afstand tot het gemiddelde | Stap 3 + 4: Gekwadrateerde afstand |
|---|---|---|
| 72 | 72 – 207,5 = -135,5 | 18360,25 |
| 110 | 110 – 207,5 = -97,5 | 9506,25 |
| 134 | 134 – 207,5 = -73,5 | 5402,25 |
| 190 | 190 – 207,5 = -17,5 | 306,25 |
| 238 | 238 – 207,5 = 30,5 | 930,25 |
| 287 | 287 – 207,5 = 79,5 | 6320,25 |
| 305 | 305 – 207,5 = 97,5 | 9506,25 |
| 324 | 324 – 207,5 = 116,5 | 13572,25 |
| Gemiddelde = 207,5 | Som = 0 | Som van de kwadraten (sum of squares) = 63904 |
n – 1 = 7
63904 / 7 = 9129,14
s = √9129,14 = 95,54
De standaarddeviatie van je data is 95,54. Dit betekent dat iedere score gemiddeld genomen 95,54 van het gemiddelde verwijderd is.
Formule voor de standaarddeviatie van populaties
Als je data hebt voor ieder lid van de populatie, gebruik je deze formule voor de standaarddeviatie:
| Formule | Uitleg |
|---|---|
|
Formule voor de standaarddeviatie van steekproeven
Als je data hebt verzameld voor een steekproef, gebruik je deze formule voor de standaarddeviatie:
| Formule | Uitleg |
|---|---|
|
Waarom gebruik je n – 1 voor de standaarddeviatie van een steekproef?
Als je populatiedata hebt verzameld, kun je een exacte waarde berekenen voor de standaarddeviatie van de populatie, De standaarddeviatie weerspiegelt in dit geval de precieze hoeveelheid spreiding (variabiliteit), omdat je data hebt verzameld voor ieder lid van de populatie.
Als je steekproefdata hebt gebruikt, is de standaarddeviatie van deze steekproef altijd een schatting van de standaarddeviatie voor de populatie. Als je in deze formule simpelweg n zou gebruiken, onderschat je daarmee in de meeste gevallen de spreiding.
Door de steekproef n te verkleinen tot n – 1, wordt de standaarddeviatie verhoogd, waardoor je een betere, strengere (conservatieve) schatting van de spreiding krijgt.
Hoewel deze schatting alsnog gepaard gaat met een bias, levert de methode een minder vertekende schatting van de standaarddeviatie op. Het is beter om de spreiding te overschatten dan te onderschatten.
Het verschil tussen de vertekende (biased) en strenge schattingen van de standaarddeviatie wordt kleiner als je steekproefgrootte toeneemt.
Variantie (variance)
De variantie is het rekenkundig gemiddelde van de gekwadrateerde afwijkingen tot het gemiddelde. Je bepaalt de variantie door de standaarddeviatie te kwadrateren.
Het is moeilijk om de variantie te interpreteren, maar toch is deze maat erg belangrijk als je verschillende datasets wilt vergelijken met statistische toetsen, zoals een ANOVA.
Variantie weerspiegelt de mate van spreiding in de dataset. Hoe meer de data verspreid zijn, des te groter de variantie ten opzichte van het gemiddelde.
s = 95,5
s2 = 95,5 * 95,5 = 9129,14
De variantie is 9129,14.
Om de variantie handmatig te berekenen, voer je alle stappen voor de standaarddeviatie uit, met nog een extra laatste stap.
Formule voor de variantie van populaties
| Formule | Uitleg |
|---|---|
|
Formule voor de variantie van steekproeven
| Formule | Uitleg |
|---|---|
|
Wat is de beste spreidingsmaat?
De beste spreidingsmaat is afhankelijk van het meetniveau en de verdeling.
Meetniveau
Voor ordinale data zijn het bereik en de interkwartielafstand de enige bruikbare spreidingsmaten. Voor interval- of ratiodata is het ook mogelijk om de standaarddeviatie en variantie te berekenen.
Verdeling
Voor normale verdelingen kun je alle spreidingsmaten gebruiken. De standaarddeviatie en variantie geven de meeste informatie, omdat hiervoor de gehele dataset wordt gebruikt. Dit betekent echter ook dat ze worden beïnvloed door uitbijters (ook wel uitschieters genoemd).
Voor scheve verdelingen of datasets met uitbijters kun je het beste de interkwartielafstand gebruiken. Deze maat wordt het minst beïnvloed door extreme waarden, omdat je hiervoor datapunten gebruikt uit het midden van de dataset. Extreme waarden bevinden zich aan de uiteinden.
Veelgestelde vragen
- Wat zijn de vier meest gebruikte spreidingsmaten?
-
De spreiding (variability) wordt meestal bepaald met de volgende descriptieve statistieken:
- Bereik (range): het verschil tussen de hoogste en laagste waarde uit de dataset.
- Interkwartielafstand (interquartile range): het bereik van het middelste deel van de dataset.
- Standaarddeviatie (standard deviation): de gemiddelde afstand tussen iedere waarde in de dataset en het gemiddelde.
- Variantie (variance): de standaarddeviatie in het kwadraat.
- Wat is het verschil tussen centrummaten en spreidingsmaten?
-
Centrummaten zeggen iets over het punt waar de meeste waarden geclusterd zijn (het midden of het centrum van je dataset). Spreidingsmaten geven informatie over de afstand tussen datapunten (hoe verspreid zijn de data).
Datasets kunnen dezelfde centrale tendens hebben en een verschillende mate van spreiding (of andersom). Door beide soorten maten te combineren, krijg je een compleet beeld van je data.
- Wat is het verschil tussen beschrijvende en toetsende statistiek?
-
Met beschrijvende statistiek (ook wel descriptieve statistiek genoemd) vat je de kenmerken van een dataset samen. Met toetsende statistiek (ook wel inferentiële of verklarende statistiek genoemd) toets je een hypothese of bepaal je of je data generaliseerbaar zijn naar een bredere populatie.
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Merkus, J. (2021, 02 november). Spreidingsmaten: Bereik, standaarddeviatie, variantie en meer. Scribbr. Geraadpleegd op 9 december 2024, van https://www.scribbr.nl/statistiek/spreidingsmaten/