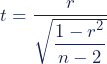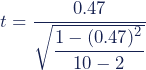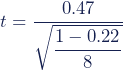Pearson Correlatiecoëfficiënt (r) Berekenen en Interpreteren
De Pearson correlatiecoëfficiënt (Pearson correlation coefficient), aangeduid met r, is de meest gebruikelijke manier om een lineaire correlatie te meten. Het is een getal tussen de -1 en 1 dat de sterkte en de richting van het verband tussen twee variabelen meet.
| Pearson correlatie coëfficiënt (r) | Soort correlatie | Interpretatie | Voorbeeld |
|---|---|---|---|
| Tussen 0 en 1 | Positieve correlatie | Als één variabele verandert, verandert de andere variabele in dezelfde richting. | Lengte en gewicht van baby’s:
Hoe langer de baby, hoe zwaarder hun gewicht. |
| 0 | Geen correlatie | Er is geen verband tussen de variabelen. | Prijs van de auto en de breedte van de ruitenwissers:
De prijs van een auto houdt geen verband met de breedte van de ruitenwissers. |
| Tussen 0 en –1 |
Negatieve correlatie | Als één variabele verandert, verandert de andere variabele in de tegengestelde richting. | Hoogte en luchtdruk:
Hoe hoger je bent, hoe lager de luchtdruk. |
Wat is de Pearson correlatiecoëfficiënt?
De Pearson correlatiecoëfficiënt (r) is de meest gebruikte correlatiecoëfficiënt en is bekend onder vele namen:
- Pearson’s r
- Bivariate correlatie
- Pearson product-moment correlatiecoëfficiënt (PPMCC)
- De correlatiecoëfficiënt
De Pearson correlatie is een beschrijvende statistiek, wat betekent dat de correlatie de kenmerken van een dataset samenvat. De Pearson correlatie beschrijft de sterkte en de richting van het lineaire verband tussen twee kwantitatieve variabelen.
Hoewel de interpretaties van de sterkte van het verband (ook wel effectgrootte genoemd) van vakgebied tot vakgebied verschillen, geeft onderstaande tabel de algemene vuistregels:
| Waarde van de Pearson correlatie coëfficiënt (r) | Sterkte | Richting |
|---|---|---|
| Groter dan .5 | Sterk | Positief |
| Tussen .3 en .5 | Matig | Positief |
| Tussen 0 en .3 | Zwak | Positief |
| 0 | Geen | Geen |
| Tussen 0 en –.3 | Zwak | Negatief |
| Tussen –.3 en –.5 | Matig | Negatief |
| Groter dan –.5 | Sterk | Negatief |
De Pearson correlatie is ook een inferentiële (toetsende of verklarende) statistiek, wat betekent dat deze kan worden gebruikt voor hypothesetoetsing. Met de correlatie kan worden nagegaan of er een significant verband bestaat tussen twee variabelen.
Met de Pearson correlatie kun je dus niet zeggen of de ene variabele de andere veroorzaakt.
Pearson correlatie visualiseren
Een andere manier om over de Pearson correlatie (r) na te denken is als een maatstaf voor hoe dicht de observaties bij een best passende lijn (line of best fit) liggen.
De Pearson correlatie vertelt je ook of de helling van de best passende lijn negatief of positief is. Als de helling negatief is, is r negatief. Als de helling positief is, is r positief.
Als r 1 of -1 is, vallen alle observaties precies op de best passende lijn:
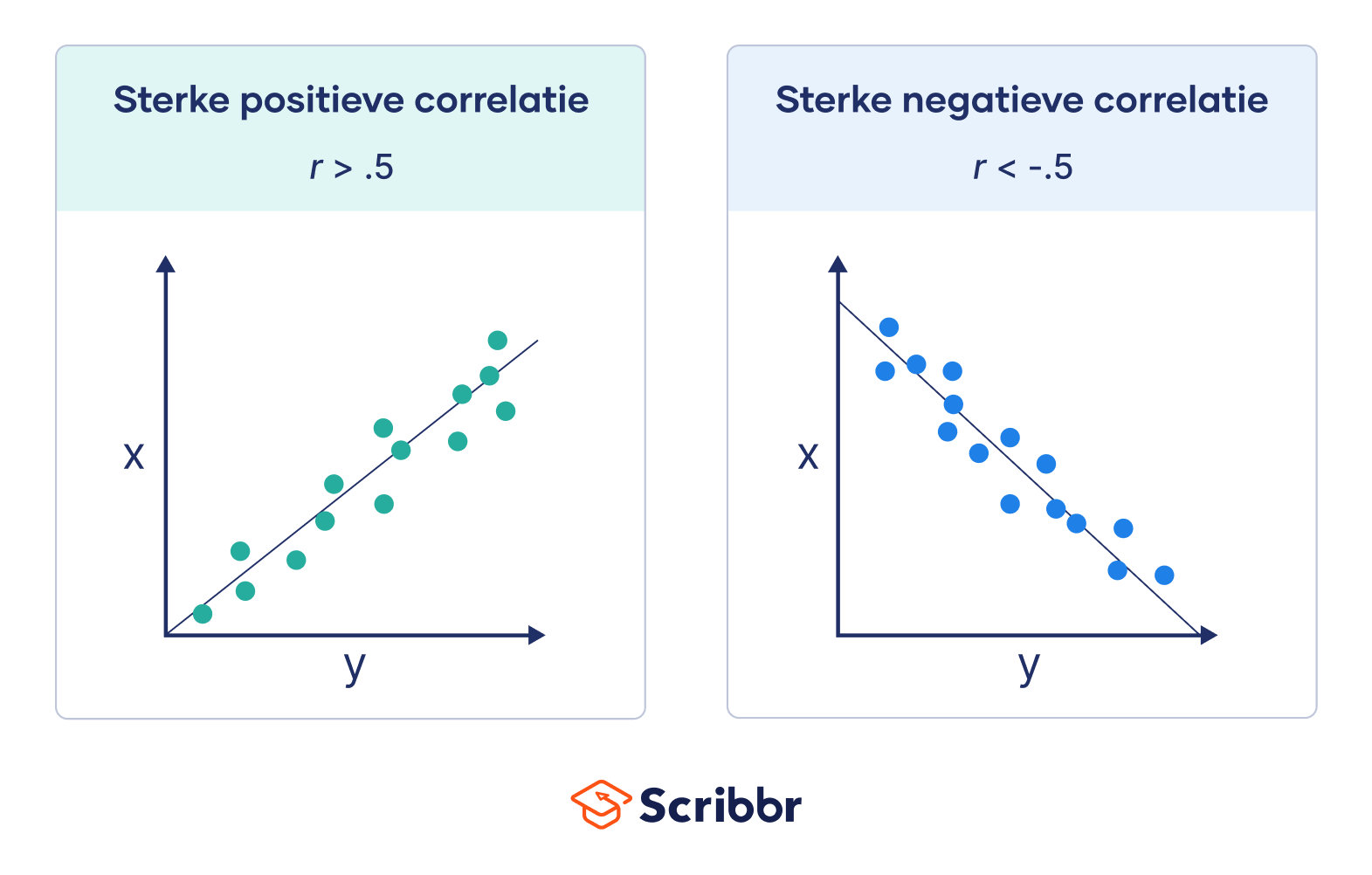
Als r groter is dan .5 of kleiner dan -.5, liggen de observatiepunten dicht bij de best passende lijn:
Als r tussen 0 en .3 of tussen 0 en -.3 ligt, liggen de observatiepunten ver van de best passende lijn:
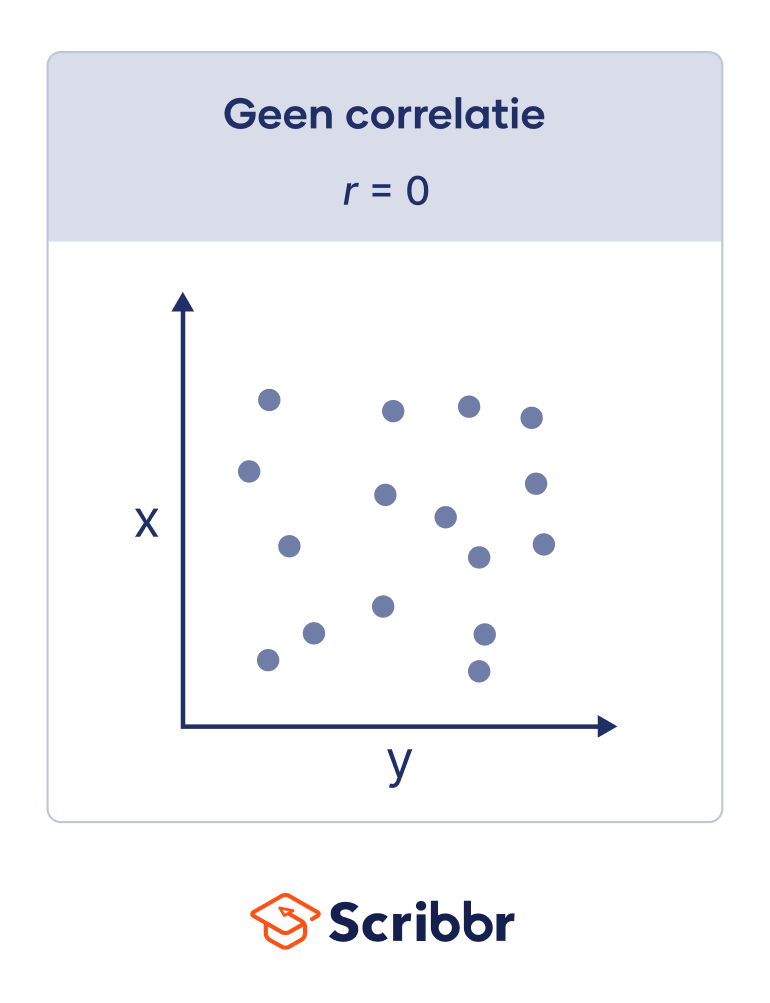
Als r 0 is, is een best passende lijn niet behulpzaam om het verband tussen de variabelen te beschrijven:
Wanneer gebruik je de Pearson correlatie?
De Pearson correlatie (r) is één van de verschillende correlatiecoëfficiënten waartussen je moet kiezen als je een correlatie wilt meten. De Pearson correlatie is een goede keuze als alle onderstaande punten waar zijn:
- Beide variabelen zijn kwantitatief: Je zult een andere methode moeten gebruiken als minstens één van de variabelen kwalitatief is.
- Beide variabelen zijn continu: Discrete variabelen kunnen enkel worden uitgedrukt in telbare, ronde getallen (e.g., 1,2,3). Continue variabelen kunnen elke waarde aannemen (e.g., 1.25, 3.491, 4.3327).
- De variabelen zijn normaal verdeeld: Je kunt van elke variabele een histogram maken om na te gaan of de verdeling bij benadering normaal zijn. Het is geen probleem als de variabelen een beetje niet-normaal verdeeld zijn.
- De data hebben geen uitschieters (outliers): Uitschieters of uitbijters zijn observaties die niet dezelfde patronen volgen als de rest van de data. Aan de hand van een scatterplot kun je controleren of er uitschieters zijn. Je kijkt dan naar observatiepunten die ver van de rest afliggen.
- De relatie is lineair: “Lineair” betekent dat de relatie tussen twee variabelen redelijk goed kan worden beschreven door een rechte lijn. Je kunt een scatterplot gebruiken om te zien of het verband tussen twee variabelen lineair is.
Pearson vs Spearmans rangcorrelatiecoëfficiënt
Spearmans rangcorrelatiecoëfficiënt is een andere veelgebruikte correlatiecoëfficiënt. Het is een betere keuze dan de Pearson correlatie als één of meer van de volgende punten waar zijn:
- De variabelen zijn van ordinaal meetniveau.
- De variabelen zijn niet-normaal verdeeld.
- De data bevatten uitschieters.
- Het verband tussen de variabelen is niet-lineair en monotoon.
Pearson correlatie berekenen
Dit is de formule voor het berekenen van de Pearson correlatie (r):
De formule is makkelijk te gebruiken als je onderstaand stappenplan volgt. Je kunt ook software zoals R of Excel gebruiken om de Pearson correlatie voor je te laten berekenen.
| Gewicht (kg) | Lengte (cm) |
|---|---|
| 3.63 | 53.1 |
| 3.02 | 49.7 |
| 3.82 | 48.4 |
| 3.42 | 54.2 |
| 3.59 | 54.9 |
| 2.87 | 43.7 |
| 3.03 | 47.2 |
| 3.46 | 45.2 |
| 3.36 | 54.4 |
| 3.3 | 50.4 |
Stap 1: Bereken de som van x en de som van y
Start met het hernoemen van de variabelen naar “x” en “y”. Het maakt niet uit welke variabele x heet en welke variabele y. De formule zal op beide manieren hetzelfde antwoord geven.
Ook maakt het niet uit in welke eenheden de variabelen staan uitgedrukt (e.g., kilogram, pond, percentages, etc.). Het antwoord wordt niet beïnvloed door de eenheden van de variabelen.
Tel vervolgens alle waarden van x bij elkaar op, en alle waarden van y. In de formule wordt deze stap aangegeven met het symbool Σ, wat “neem de som van” betekent.
Lengte = y
Σx = 3.63 + 3.02 + 3.82 + 3.42 + 3.59 + 2.87 + 3.03 + 3.46 + 3.36 + 3.30
Σx = 33.5
Σy = 53.1 + 49.7 + 48.4 + 54.2 + 54.9 + 43.7 + 47.2 + 45.2 + 54.4 + 50.4
Σy = 501.2
Stap 2: Bereken x2 en y2 en hun sommen
Maak twee nieuwe kolommen die de kwadraten van x en y weergeven. Neem vervolgens weer de sommen van deze kolommen.
| x | y | x2 | y2 |
|---|---|---|---|
| 3.63 | 53.1 | (3.63)2 = 13.18 | (53.1)2 = 2 819.6 |
| 3.02 | 49.7 | 9.12 | 2 470.1 |
| 3.82 | 48.4 | 14.59 | 2 342.6 |
| 3.42 | 54.2 | 11.7 | 2 937.6 |
| 3.59 | 54.9 | 12.89 | 3 014 |
| 2.87 | 43.7 | 8.24 | 1 909.7 |
| 3.03 | 47.2 | 9.18 | 2 227.8 |
| 3.46 | 45.2 | 11.97 | 2 043 |
| 3.36 | 54.4 | 11.29 | 2 959.4 |
| 3.3 | 50.4 | 10.89 | 2 540.2 |
Σx2 = 13.18 + 9.12 + 14.59 + 11.70 + 12.89 + 8.24 + 9.18 + 11.97 + 11.29 + 10.89
Σx2 = 113.05
Σy2 = 2 819.6 + 2 470.1 + 2 342.6 + 2 937.6 + 3 014.0 + 1 909.7 + 2 227.8 + 2 043.0 + 2 959.4 + 2 540.2
Σy2 = 25 264
Stap 3: Bereken het kruisproduct en tel de waarden op
In een laatste kolom vermenigvuldig je x en y met elkaar (dit heet ook wel het kruisproduct). Vervolgens tel je weer de waarden van deze kolom bij elkaar op.
| x | y | x2 | y2 | xy (x*y) |
|---|---|---|---|---|
| 3.63 | 53.1 | 13.18 | 2 819.6 | 3.63 * 53.1 = 192.8 |
| 3.02 | 49.7 | 9.12 | 2 470.1 | 150.1 |
| 3.82 | 48.4 | 14.59 | 2 342.6 | 184.9 |
| 3.42 | 54.2 | 11.7 | 2 937.6 | 185.4 |
| 3.59 | 54.9 | 12.89 | 3 014 | 197.1 |
| 2.87 | 43.7 | 8.24 | 1 909.7 | 125.4 |
| 3.03 | 47.2 | 9.18 | 2 227.8 | 143 |
| 3.46 | 45.2 | 11.97 | 2 043 | 156.4 |
| 3.36 | 54.4 | 11.29 | 2 959.4 | 182.8 |
| 3.3 | 50.4 | 10.89 | 2 540.2 | 166.3 |
Σxy = 192.8 + 150.1 + 184.9 + 185.4 + 197.1 + 125.4 + 143.0 + 156.4 + 182.8 + 166.3
Σxy = 1 684.2
Stap 4: Bereken r
Gebruik de formule en de getallen die je in de vorige stappen hebt berekend om r te vinden.

Toetsen op de significantie van de Pearson correlatie
De Pearson correlatie kan ook worden gebruikt om te toetsen of het verband tussen twee variabelen significant is.
De Pearson correlatie van de steekproef is r. Het is een schatting van rho (ρ), de Pearson correlatie van de populatie. Als je r en n (de steekproefgrootte) kent, kun je afleiden of ρ significant verschillend is van 0 (geen verband).
- Nulhypothese (H0): ρ = 0
- Alternatieve hypothese (Ha): ρ ≠ 0
Om de hypothesen te toetsen, kun je gebruikmaken van software zoals R of Stata, of je kunt de hypothesetoetsing handmatig uitvoeren door de onderstaande drie stappen te volgen.
Stap 1: Bereken de t-waarde
Bereken de t-waarde (een teststatistiek) met deze formule:
Stap 2: Vind de kritieke waarde van t
Je kunt de kritieke waarde van t (t*) vinden in een t-tabel. Om de t-tabel te gebruiken, moet je drie dingen weten:
- Vrijheidsgraden (df): Voor de Pearson correlatietoets is de formule df = n – 2.
- Significantieniveau (α): Normaal gesproken is het significantieniveau .05.
- Eenzijdig (one-tailed) of tweezijdig (two-tailed): Meestal is een tweezijdige toets een goede keuze voor de Pearson correlatie.
Stap 3: Vergelijk de t-waarde met de kritieke waarde
Bepaalde of de absolute t-waarde groter is dan de kritieke waarde van t. “Absoluut” betekent dat je het minteken moet negeren als de t-waarde negatief is.
t* = 1.86
De t-waarde is kleiner dan de kritieke waarde van t.
Stap 4: Beslis of de nulhypothese verworpen moet worden
- Als de t-waarde groter is dan de kritieke waarde, dan is het verband statistisch significant (p < α). De data tonen aan dat de nulhypothese verworpen kan worden en de alternatieve hypothese kan worden ondersteund.
- Als de t-waarde kleiner is dan de kritieke waarde, dan is het verband niet statistisch significant (p > α). De data tonen niet aan dat de nulhypothese verworpen kan worden en bieden geen ondersteuning voor de alternatieve hypothese.
Daarom wordt de nulhypothese dat de Pearson correlatie van de populatie (ρ) 0 is niet verworpen. Er is geen significant verband tussen gewicht en lengte (p > .05).
(Merk op dat de steekproef van 10 heel erg klein is. Het is mogelijk dat je een significant verband kan vinden als je de steekproefgrootte uitbreidt.)
Pearson correlatie rapporteren
Als je besluit om een Pearson correlatie (r) in je paper of scriptie op te nemen, moet je dat in je onderzoeksresultaten vermelden. Je kunt deze regels volgen als je statistieken in APA-stijl wilt rapporteren:
- Het is niet nodig om een referentie of formule toe te voegen, aangezien de correlatiecoëfficiënt een veelgebruikte statistiek is.
- Cursiveer r wanneer je de waarde rapporteert.
- Voeg nooit een voorloopnul toe (een nul voor het decimale punt), want de correlatiecoëfficiënt kan niet groter dan 1 of kleiner dan -1 zijn.
- Achter de decimale punt dienen twee significante getallen te staan.
Als de Pearson correlatie wordt gebruikt als inferentiële statistiek (om te toetsen of het verband significant is), dan wordt de r meestal gerapporteerd in combinatie met de vrijheidsgraden en p-waarde. De vrijheidsgraden staan tussen haakjes naast r.
Veelgestelde vragen over Pearson correlatiecoëfficiënt
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
Scharwächter, V. (2022, 17 augustus). Pearson Correlatiecoëfficiënt (r) Berekenen en Interpreteren. Scribbr. Geraadpleegd op 9 juli 2025, van https://www.scribbr.nl/statistiek/pearson-correlatie/

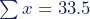
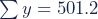
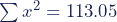
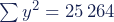
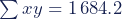
![Rendered by QuickLaTeX.com r = \frac{ n\sum{xy}-(\sum{x})(\sum{y})}{% \sqrt{[n\sum{x^2}-(\sum{x})^2][n\sum{y^2}-(\sum{y})^2]}}](https://www.scribbr.nl/wp-content/ql-cache/quicklatex.com-ab89c0ce832838d8e949743001780a76_l3.png)
![Rendered by QuickLaTeX.com r = \frac{ 10\sum{1\,684.2}-(33.5)(501.2)}{% \sqrt{[(10)(113.05)-(33.5)^2][(10)(25\,264)-(501.2)^2]}}](https://www.scribbr.nl/wp-content/ql-cache/quicklatex.com-afe81c87b865bc391c72805b2a147642_l3.png)
![Rendered by QuickLaTeX.com r = \frac{ 16\,842-16\,790.2)}{% \sqrt{[1\,130.5-1\,122.25][252\,640-251\,201.4]}}](https://www.scribbr.nl/wp-content/ql-cache/quicklatex.com-a93d69120752d4a79c1cd3bc22266aff_l3.png)