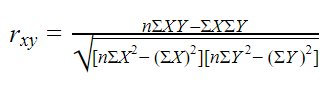Wat is de effectgrootte en waarom is deze van belang?

Vertaald op 5 november 2021 door Julia Merkus. Oorspronkelijk gepubliceerd door Pritha Bhandari

De effectgrootte (effect size) laat zien hoe betekenisvol de relatie tussen variabelen of het verschil tussen groepen is. Het zegt iets over de praktische relevantie (ook wel praktische significantie genoemd) van een onderzoeksresultaat.

Als een effect groot is, heeft het onderzoeksresultaat praktische implicaties, terwijl een klein effect waarschijnlijk ook maar beperkte praktische implicaties heeft.

Let op

In het Nederlands gebruik je de komma als decimaalteken, maar bij het rapporteren van statistische resultaten is het gebruikelijk om de punt als decimaalteken te gebruiken. Ook wordt vaak de 0 voor het decimaalteken weggelaten (.05 in plaats van 0.05).

Inhoudsopgave

Waarom is de effectgrootte van belang?
Hoe bereken je de effectgrootte?
Hoe weet je of een effect klein of groot is?
Wanneer bereken je een effectgrootte?
Veelgestelde vragen

Waarom is de effectgrootte van belang?

Statistische significantie laat zien dat het onwaarschijnlijk is dat een effect, relatie of verschil alleen door toeval of willekeurige factoren kan worden verklaard. Praktische relevantie laat zien of het effect groot genoeg is om daadwerkelijk betekenisvol te zijn in de echte wereld. Statistische significantie wordt aangegeven met een p-waarde, terwijl je voor praktische relevantie een effectgrootte rapporteert.

Statistische significantie kan misleidend zijn, omdat de p-waarde kan worden beïnvloed door de steekproefomvang. Als je de steekproef vergroot, is de kans groter dat je een statistisch significant resultaat vindt, zelfs als het effect in werkelijkheid heel klein is.

Effectgroottes worden niet beïnvloed door de steekproefomvang. Je gebruikt enkel de data om de effectgrootte te berekenen.

Daarom is het belangrijk om naast de p-waarde ook de effectgrootte te rapporteren, zodat de resultaten beter kunnen worden geïnterpreteerd. De APA-richtlijnen vereisen waar mogelijk rapportage van effectgroottes en betrouwbaarheidsintervallen (confidence intervals).

Voorbeeld: Statistische significantie versus praktische relevantie

In een groot onderzoek werden twee methoden voor gewichtsverlies vergeleken. Er zaten 13.000 deelnemers in een experimentele interventiegroep en 13.000 participanten in de controlegroep. De participanten in de controlegroep gebruikten een wetenschappelijk onderbouwde methode voor gewichtsverlies, terwijl de experimentele groep een nieuwe app gebruikte.

Na 6 maanden was het gemiddelde gewichtsverlies (in kg) voor de experimentele groep (M = 10,6, SD = 6,7) net iets hoger dan het gemiddelde gewichtsverlies voor de controlegroep (M = 10,5, SD = 6,8).

Deze resultaten waren statistisch significant (p = 0.01) door de grote steekproefomvang. In de praktijk is een verschil van slechts 0.1 kg echter verwaarloosbaar en betekent het niet dat de ene methode de voorkeur verdient boven de andere.

Een effectgrootte zou kunnen aangeven hoe veelbelovend de nieuwe methode daadwerkelijk is ten opzichte van de traditionele methode.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Hoe bereken je de effectgrootte?

Er zijn tientallen maten voor de effectgrootte. De meest voorkomende effectgroottes zijn Cohen’s d en Pearson’s correlatiecoëfficiënt r. Cohen’s d meet de grootte van het verschil tussen twee groepen, terwijl Pearson’s r de sterkte van de relatie tussen twee variabelen meet.

Cohen’s d

Cohen’s d is ontworpen om twee groepen te vergelijken. Voor deze maat wordt het verschil tussen twee gemiddelden uitgedrukt in standaarddeviatie-eenheden. Cohen’s d vertelt je hoeveel standaarddeviaties tussen de twee gemiddelden liggen.

Formule Cohen’s d	Uitleg
	x̄₁= gemiddelde van Groep 1 x̄₂= gemiddelde van Groep 2 s = standaarddeviatie

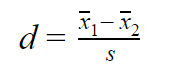De keuze voor het soort standaarddeviatie in de vergelijking hangt af van je onderzoeksopzet. Je kunt de volgende standaarddeviaties gebruiken:

Een pooled standaarddeviatie is gebaseerd op de data van beide groepen.
De standaarddeviatie van een controlegroep kan worden gebruikt als je design een controlegroep en een experimentele groep bevat.
De standaarddeviatie van de pretest-data kan worden gebruikt als je within-subjects design een pretest en posttest bevat.

Voorbeeld: Cohen’s d berekenen

Om effectgrootte Cohen’s d te berekenen voor het onderzoek naar gewichtsverlies, neem je de gemiddelden van beide groepen en de standaarddeviatie van de controlegroep.

d = (x̄₁ − x̄₂) ÷ s

d = (10.6 − 10.5 )÷ 6.8 = 0.015

Een Cohen’s d van 0.015 laat zien dat het significante resultaat weinig tot geen praktische relevantie heeft.

Pearson’s r

Pearson’s r (ook wel de correlatiecoëfficiënt genoemd) meet de sterkte van een lineair verband tussen twee variabelen. Hiermee wordt berekend hoeveel variabiliteit van de ene variabele wordt bepaald door de variabiliteit van de andere variabele.

De formule is vrij complex, dus het beter om Pearson’s r automatisch te laten berekenen door de software die je gebruikt om de statistische toetsen uit te voeren (zoals SPSS).

Formule Pearson’s r	Uitleg
	r_xy= sterkte van de correlatie tussen variabele x en y n = steekproefomvang ∑ = som X = iedere waarde voor de x-variabele Y = iedere waarde voor de y-variabele XY = het product van iedere x-variabele-score vermenigvuldigd met de corresponderende y-variabele-score

Formule Pearson’s r

Uitleg

r_xy= sterkte van de correlatie tussen variabele x en y
n = steekproefomvang
∑ = som
X = iedere waarde voor de x-variabele
Y = iedere waarde voor de y-variabele
XY = het product van iedere x-variabele-score vermenigvuldigd met de corresponderende y-variabele-score

Pearson’s r is een gestandaardiseerde maat om correlaties tussen variabelen te meten, waardoor de maat geen eenheid heeft. Je kunt de sterkte van alle correlaties direct met elkaar vergelijken.

Let op

Je kunt Pearson’s r en Cohen’s d alleen gebruiken voor interval- of ratiovariabelen. Als je nominale of ordinale variabelen hebt, moet je andere maten voor de effectgrootte gebruiken.

Hoe weet je of een effect klein of groot is?

Je interpreteert de effectgrootte voor Cohen’s d op basis van de bijbehorende criteria (Cohen’s criteria). Er wordt onderscheid gemaakt tussen een klein, medium en groot effect.

Effectgrootte	Cohen’s d	Pearson’s r
Klein	0.2	0.1 tot 0.3 of -0.1 tot -0.3
Medium	0.5	0.3 tot 0.5 of -0.3 to -0.5
Groot	0.8 of hoger	0.5 of hoger of -0.5 of lager

Cohen’s d kan elke waarde tussen 0 en oneindig aannemen. Over het algemeen geldt: hoe groter Cohen’s d, des te groter het effect.

Pearson’s r kan enkel waarden aannemen tussen de -1 en 1. Hiervoor geldt:

Hoe dichter de waarde bij 0 ligt, des te kleiner het effect.
Hoe dichter de waarde bij -1 of 1 ligt, des te groter het effect.
Een positieve waarde wijst op een positieve correlatie (beide variabelen nemen samen toe of af).
Een negatieve waarde wijst op een negatieve correlatie (als de ene variabele afneemt, neemt de andere toe, en andersom).

De criteria voor interpretatie van de effectgrootte kunnen ook afhangen van wat gebruikelijk wordt gevonden in jouw specifieke vakgebied, dus zorg ervoor dat je andere artikelen raadpleegt bij het interpreteren van de effectgrootte.

Wanneer bereken je een effectgrootte?

Het is handig om de effectgrootte te berekenen, zowel voordat je begint met je onderzoek als na de dataverzameling.

Voordat je je onderzoek start

Als je de verwachte effectgrootte hebt berekend, kun je de minimale steekproefomvang bepalen die je nodig hebt voor voldoende statistische power om een effect van die grootte te detecteren.

In de statistiek verwijst power naar de waarschijnlijkheid dat een hypothesetoets een echt effect vaststelt als dat effect er is. Dit noem je ook wel het onderscheidend vermogen. Een toets met veel statistische power (statistical power) is beter in staat een Type II-fout (false negative) te voorkomen.

Als je onderzoek niet voldoende power heeft, kan het voorkomen dat je geen statistisch significant resultaat vindt, zelfs als dit wel aanwezig is en praktische relevantie heeft. Hierdoor zou je ten onrechte de nulhypothese behouden.

Met behulp van een poweranalyse kun je de verwachte effectgrootte en het gekozen significantieniveau gebruiken om de steekproefomvang te bepalen die nodig is voor een bepaalde mate van power.

Na de dataverzameling

Nadat je de data hebt verzameld, kun je de werkelijke effectgrootte berekenen en rapporteren in de samenvatting en de resultatensectie van je onderzoek.

Effectgroottes vormen de ruwe data in meta-analyses, omdat ze gestandaardiseerd zijn, waardoor ze makkelijk kunnen worden vergeleken. Met een meta-analyse kun je de effectgroottes van veel vergelijkbare onderzoeken combineren om een idee te krijgen van de gemiddelde effectgrootte van een specifiek resultaat.

Als je een meta-analyse uitvoert, kun je ook een stap verder gaan door te suggereren waarom de effectgroottes verschillen. Dit kan nieuwe ideeën voor onderzoek opleveren.