Hoe kun je het gemiddelde berekenen? | Uitleg & Voorbeelden

Het rekenkundig gemiddelde (mean) van een dataset is de som van alle waarden, gedeeld door het totale aantal waarden. Dit is de meest gebruikte centrummaat, gevolgd door de mediaan en modus.

Gemiddelde berekenen

Je kunt het gemiddelde met de hand berekenen of met behulp van onze gemiddelde calculator hieronder.

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

Formules voor steekproef- en populatiegemiddelden

Bij onderzoek verzamel je vaak data voor een steekproef en gebruik je toetsende statistiek (ook wel inferentiële of verklarende statistiek genoemd) om inzicht te krijgen in de populatie waar de steekproef deel van uitmaakt.

De formules voor het steekproefgemiddelde en het populatiegemiddelde verschillen alleen in wiskundige notatie. Voor de populatieformule gebruik je hoofdletters, terwijl je voor de steekproefformule kleine letters gebruikt.

Populatiegemiddelde

Formule voor populatiegemiddelde	Uitleg
	= populatiegemiddelde  = som van alle waarden in de populatie = aantal waarden in de populatie

Het populatiegemiddelde kan ook worden aangeduid met de Griekse letter μ.

Steekproefgemiddelde

Formule voor steekproefgemiddelde	Uitleg
	= steekproefgemiddelde  = som van alle waarden in de steekproef = aantal waarden in de populatie

Het steekproefgemiddelde kan ook worden aangeduid met M.

Stappen om het gemiddelde te berekenen

Er zijn twee stappen om het gemiddelde te berekenen:

1. Tel alle waarden in de dataset bij elkaar op (de som).
2. Deel dit getal door het aantal waarden.

We zullen deze stappen doorlopen met een voorbeeld.

Stel je wilt weten hoeveel euro mensen gemiddeld uitgeven aan een etentje voor twee in jouw buurt. Je vraagt een steekproef van 8 buren hoeveel ze de laatste keer dat ze uit eten gingen hebben uitgegeven, en je bepaalt de gemiddelde kosten.

Stap 1: Bepaal de som van de waarden door ze bij elkaar op te tellen

Er is sprake van een steekproef, dus we gebruiken de formule voor het steekproefgemiddelde.

Formule	Berekening
	42 + 13 + 31 + 87 + 24 + 58 + 76 + 69 = 400

Stap 2: Deel de som door het aantal waarden in de dataset

In deze formule is n het aantal waarden in je dataset. Onze dataset heeft 8 waarden.

Formule	Berekening

Het gemiddelde vertelt ons dat participanten uit onze steekproef gemiddeld €50,00 uitgaven aan een etentje voor twee.

Het effect van uitbijters op het gemiddelde

Uitbijters (ook wel uitschieters of outliers genoemd) zijn extreme waarden die afwijken van de meeste andere waarden in de dataset. Aangezien je voor de berekening van het gemiddelde alle waarden gebruikt, kan een uitbijter het gemiddelde heel makkelijk beïnvloeden. Hierdoor wijkt het gemiddelde soms sterk af van de meerderheid van de waarden.

Om dit te illustreren, voegen we een uitbijter toe aan de dataset.

Stap 1: Bepaal de som van de waarden door ze bij elkaar op te tellen

Formule	Berekening
	42 + 13 + 31 + 87 + 24 + 58 + 76 + 69 + 230 = 630

Stap 2: Deel de som door het aantal waarden in de dataset

Formule	Berekening

Dit voorbeeld laat zien dat het gemiddelde met €20,00 euro toenam als gevolg van slechts één uitbijter. In dit geval zou het dus beter zijn om een andere centrummaat te gebruiken, zoals de mediaan. Het is ook een optie om de uitbijters te detecteren en systematisch te verwijderen voordat je statistieken berekent.

Wanneer gebruik je een gemiddelde, mediaan of modus?

Het gemiddelde is de meest gebruikte centrummaat, omdat deze alle waarde uit de dataset gebruikt voor de berekening. De beste maat voor de centrale tendens is afhankelijk van het soort variabele en de vorm van de verdeling.

Soort variabele

Het gemiddelde kan alleen worden berekend voor kwantitatieve variabelen (zoals lengte) en kan niet worden bepaald voor categorische variabelen (zoals geloofsovertuiging).

Voor categorische variabelen worden data vaak gecategoriseerd met behulp van labels. Je kunt er ook voor kiezen om getallen te gebruiken in plaats van labels, maar deze hebben geen betekenis. Je kunt immers zelf kiezen of je “katholiek” het label 1 en “boeddhistisch” label 2 geeft, of net andersom.

Voor categorische variabelen kun je het beste de modus zoeken, omdat je hiermee de meest populaire antwoordoptie bepaalt (de waarde met de hoogste frequentie).

Voor continue of discrete variabelen kun je wel het gemiddelde of de mediaan berekenen, omdat de getallen betekenisvol zijn.

Vorm van de verdeling

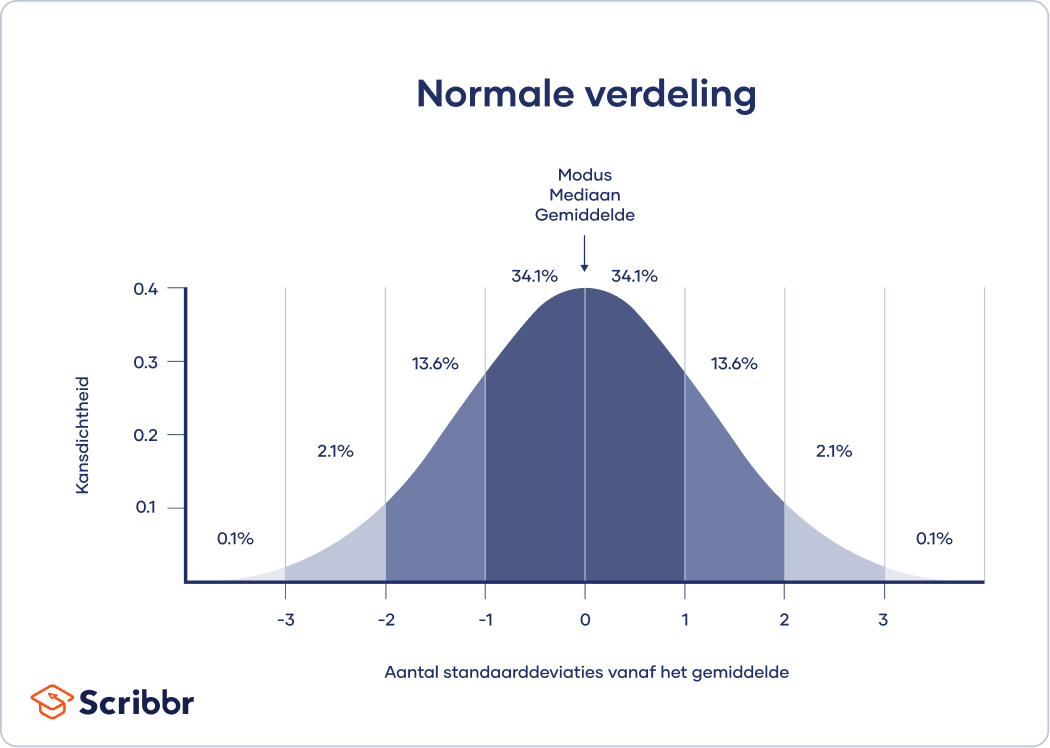
Het gemiddelde is de beste maat voor datasets met een normale verdeling (normal distribution). Bij een normale verdeling zijn de gegevens symmetrisch verdeeld zonder scheeftrekking. De meeste waarden clusteren rond een centraal gebied, waarbij het aantal waarden afneemt naarmate ze verder van het midden verwijderd zijn.

Het gemiddelde, de modus en de mediaan hebben precies dezelfde waarde bij een normale verdeling.

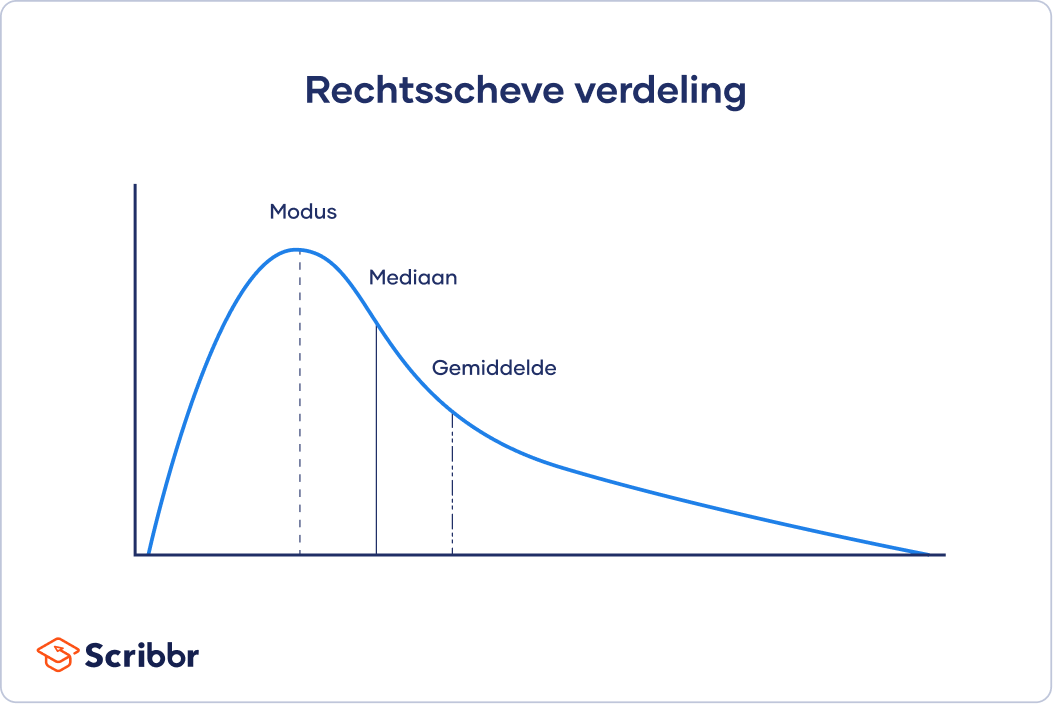
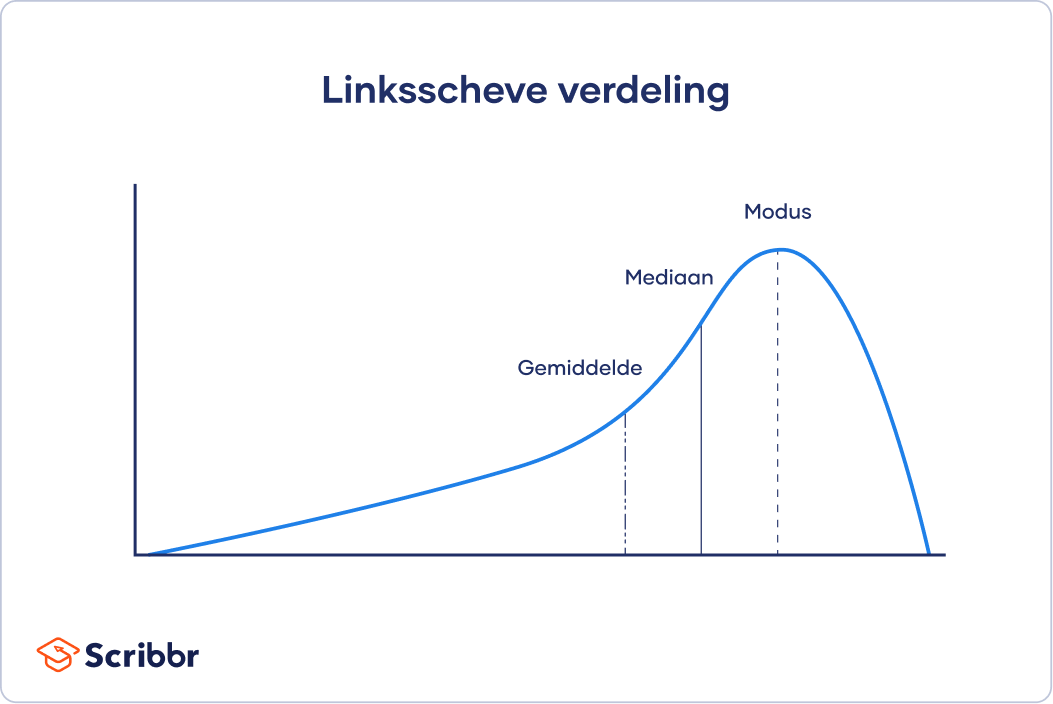
Bij scheve verdelingen (skewed distributions) bevinden zich meer waarden aan de ene kant van het centrum dan aan de andere kant. Hierdoor zijn het gemiddelde, de mediaan en de modus alle drie verschillend. Eén kant heeft een plattere, langere staart met minder scores dan aan de andere kant.

In het geval van scheve verdelingen en verdelingen met uitbijters wordt het gemiddelde makkelijk beïnvloed door extreme waarden, waardoor je geen goed beeld krijgt van de centrale tendens. De mediaan is een betere maat voor deze verdelingen, omdat je je hierbij richt op de middelste waarden en niet de extremere buitenste waarden.

Veelgestelde vragen

Hoe kun je het gemiddelde berekenen?

Je kunt het gemiddelde van een dataset vinden door de volgende twee stappen te volgen:

1. Bereken de som door alle waarden bij elkaar op te tellen.
2. Deel de som door het aantal waarden in de dataset.

Deze methode werkt zowel voor steekproef- als populatiedata. Ook maakt het niet uit of je te maken hebt met positieve (+2) of negatieve waarden (-2).

 

Wat zijn centrummaten (measures of central tendency)?

Centrummaten (measures of central tendency) helpen je het centrum of midden van een dataset te vinden.

De drie meest gebruikte centrummaten zijn het gemiddelde, de mediaan en de modus.

• De modus is de waarde die het vaakst voorkomt
• De mediaan is de middelste waarde als je de dataset van kleinste naar grootste waarde rangschikt.
• Het gemiddelde is de som van alle waarden, gedeeld door het totale aantal waarden.

Welke centrummaten kan ik gebruiken met mijn data?

Welke centrummaten je kunt gebruiken, is afhankelijk van het meetniveau en de verdeling van je data.

• Voor nominale data, kun je alleen de modus gebruiken om de meest voorkomende waarde te vinden.
• Voor ordinale data kun je zowel de modus en de mediaan gebruiken.
• Voor interval- of ratiodata kun je, naast de modus en mediaan, ook het gemiddelde gebruiken.

Ook moet je op de verdeling van je data letten. Voor normaal verdeelde data kun je alle drie de centrummaten gebruiken, maar bij scheve verdelingen is de mediaan de beste keuze.

Wat zijn de vier meetniveaus?

Meetniveaus laten zien hoe precies variabelen worden gemeten. Er zijn vier meetniveaus (of meetschalen) die van laag naar hoog kunnen worden gerangschikt.

• Nominaal: De data kunnen alleen worden gecategoriseerd (geen rangorde).
• Ordinaal: De data kunnen worden gecategoriseerd en gerangschikt.
• Interval: De data kunnen worden gecategoriseerd en gerangschikt en er zijn gelijke intervallen tussen de categorieën.
• Ratio: De data kunnen worden gecategoriseerd en gerangschikt, de intervallen zijn gelijk, en er is een absoluut of betekenisvol nulpunt.