One-Way ANOVA | Interpretatie, Uitvoering & Voorbeelden

Een one-way ANOVA toetst of de groepsgemiddelden van twee of meer groepen significant van elkaar verschillen. Hierbij wordt gebruikgemaakt van één onafhankelijke variabele.

ANOVA, wat staat voor Analysis of Variance, is een overkoepelende term voor alle soorten ANOVAs. De meest bekende ANOVAs zijn de one-way ANOVA en de two-way ANOVA.

• Een one-way ANOVA gebruikt één onafhankelijke variabele.
• Een two-way ANOVA gebruikt twee onafhankelijke variabelen.

Wanneer gebruik je een one-way ANOVA?

Je gebruikt een one-way ANOVA als je data hebt verzameld voor één categorische onafhankelijke variabele en één kwantitatieve afhankelijke variabele. De onafhankelijke variabele moet ten minste drie niveaus hebben (i.e., ten minste drie verschillende groepen of categorieën).

De ANOVA vertelt je of de afhankelijke variabele verandert als het niveau van de onafhankelijke variabele verandert. Bijvoorbeeld:

• Je onafhankelijke variabele is socialemediagebruik, en je verdeelt participanten over drie groepen met een laag, gemiddeld en hoog gebruiksniveau om te onderzoeken of er een verschil is in het aantal uren slaap per nacht.
• Je onafhankelijke variabele is het merk frisdrank, en je verzamelt data over Coca-Cola, Pepsi, Sprite en Fanta om uit te zoeken of er een verschil is in de prijs per 100 ml.
• Je onafhankelijke variabele is soort kunstmest, en je behandelt akkers met mengsels 1, 2 en 3 om uit te zoeken of er een verschil is in gewasopbrengst.

De nulhypothese (H0) van een ANOVA is dat er geen verschil is tussen de groepsgemiddelden. De alternatieve hypothese (Ha of H1) is dat ten minste één groep significant verschilt van het totale gemiddelde van de afhankelijke variabele.

Als je slechts twee groepen wilt vergelijken, kun je beter een t-toets gebruiken.

• Als je onafhankelijke variabele between-subjects varieert (alle participanten krijgen maar één van de condities aangeboden), gebruik je een ongepaarde t-test (independent t-test).
• Als je onafhankelijke variabele within-subjects varieert (alle participanten krijgen alle condities achter elkaar aangeboden), gebruik je een gepaarde t-test (dependent t-test).

Wie helpt jou met nakijken?

Betrouwbare hulptroepen vinden is niet makkelijk...

• Familie
• Vrienden
• Studiegenoten
• Scribbr

We staan altijd voor je klaar

Hoe werkt een ANOVA test?

Een ANOVA bepaalt of het verschil tussen de groepen van de onafhankelijke variabele (de niveaus) statistisch significant is door te berekenen of de gemiddelden van de groepen verschillen van het totale gemiddelde van de afhankelijke variabele.

Als één van de groepsgemiddelden significant verschilt van het totale gemiddelde, wordt de nulhypothese verworpen.

ANOVA gebruikt de F-test voor statistische significantie. Hierdoor kunnen meerdere gemiddelden tegelijkertijd worden vergeleken. Als je meerdere t-toetsen zou gebruiken voor de vergelijking van meer dan twee groepen, is er voor iedere t-toets een risico (meestal 5%) dat je een Type I-fout maakt. Door meerdere t-toetsen uit te voeren, stijgt het totale risico op een Type I-fout sterk. Dit gebeurt niet bij een ANOVA.

De F-test vergelijkt de variantie in elk groepsgemiddelde met de totale groepsvariantie. Als de variantie binnen groepen kleiner is dan de variantie tussen groepen, zal de F-test een hogere F-waarde vinden. Dit betekent dat er een grotere waarschijnlijkheid is dat het waargenomen verschil echt bestaat en dat de resultaten niet aan toeval te wijten zijn.

Aannames of assumpties voor een ANOVA

De aannames of assumpties voor een ANOVA komen grotendeels overeen met de algemene veronderstellingen van elke parametrische toets:

1. Kwantitatieve, continue afhankelijke variabele: je afhankelijke variabele moet naast kwantitatief ook continu van aard zijn, wat betekent dat het interval- of ratio-metingen zijn. Dit betekent dat de afhankelijke variabele binnen het interval- of rationiveau iedere waarde aan kan nemen.
2. Normaalverdeelde responsvariabele: de waarden van de afhankelijke variabele volgen een normale verdeling.
3. Twee of meer categorische, onafhankelijke groepen: de onafhankelijke variabele moet uit twee of meer categorische, onafhankelijke groepen (niveaus) bestaan. Het is gebruikelijker om drie of meer groepen te hebben.
4. Onafhankelijkheid van observaties: de data zijn verzameld met statistisch valide methoden, en er zijn geen verborgen relaties tussen de waarnemingen. Als je data niet aan deze aanname voldoen omdat je een confounding variabele (storende variabele) hebt waarvoor je moet controleren, gebruik je een ANOVA met blokkeringsvariabelen.
5. Geen significante outliers: de aanwezigheid van outliers kan de validiteit van de resultaten van je one-way ANOVA aantasten.
6. Homogeniteit van variantie: De variantie binnen elke groep die wordt vergeleken is voor elke groep gelijk. Als de varianties tussen de groepen verschillend zijn, is een ANOVA waarschijnlijk niet de juiste analyse voor de data.

One-way ANOVA uitvoeren

Hoewel je een ANOVA met de hand kunt uitvoeren, is het moeilijk om dat te doen met meer dan een paar waarnemingen. Hier zullen we laten zien hoe je een ANOVA analyse uitvoert met het statistische programma R, omdat het gratis, krachtig en overal beschikbaar is.

De voorbeelddataset voor het experiment over gewasopbrengst bevat data over:

• Soort kunstmest (type 1, 2 of 3)
• Plantdichtheid (1 = lage dichtheid, 2 = hoge dichtheid)
• Locatie van plant in het veld (blok 1, 2, 3 of 4)
• Uiteindelijke gewasopbrengst (in bushels per hectare)

Dit geeft ons voldoende informatie om verschillende ANOVA-toetsen uit te voeren en te zien welk model het beste bij de data past.

Voor de one-way ANOVA zullen we alleen het effect van het soort kunstmest op de gewasopbrengst analyseren.

Voorbeeld dataset voor ANOVA

Nadat je de dataset in de R-omgeving hebt geladen, kun je het commando aov()gebruiken om een ANOVA uit te voeren. In dit voorbeeld worden de verschillen in het gemiddelde van de responsvariabele, gewasopbrengst, gemodelleerd als een functie van het type kunstmest.

Hoeveel fouten bevat jouw scriptie?

De taalexperts van Scribbr verbeteren gemiddeld 150 fouten per 1000 woorden. Benieuwd wat er precies wordt verbeterd? Verschuif de cursor van links naar rechts!

Scriptie nakijken op taal

Resultaten ANOVA interpreteren

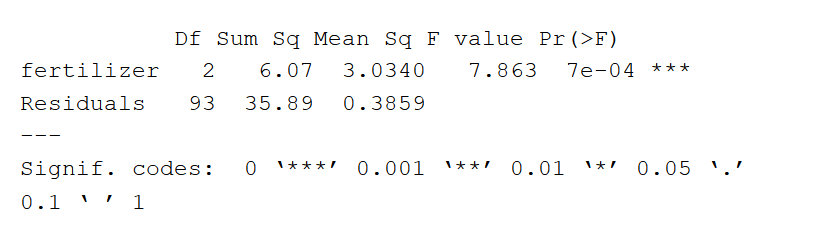
Om de samenvatting van een statistisch model in R te bekijken, gebruik je de functie summary().

De samenvatting van een ANOVA in R ziet er als volgt uit:

De ANOVA-output geeft een schatting van hoeveel variatie in de afhankelijke variabele door de onafhankelijke variabele kan worden verklaard.

• De eerste kolom vermeldt de onafhankelijke variabele samen met de modelresiduen (ook wel de modelfout genoemd).

• De kolom Df toont de vrijheidsgraden voor de onafhankelijke variabele (berekend door het aantal groepen in de variabele te nemen en daar 1 vanaf te halen), en de vrijheidsgraden voor de residuen (berekend door het totale aantal waarnemingen min 1 te nemen en daarvan het aantal groepen in elk van de onafhankelijke variabelen af te trekken).

• De kolom Sum Sq toont de som van de kwadraten (sum of squares, ook wel de totale variatie) tussen de groepsgemiddelden en het totale gemiddelde dat door die variabele wordt verklaard. De som van de kwadraten voor de variabele “kunstmest” is 6.07, terwijl de som van de residuen 35.89 is.

• De kolom Mean Sq is het gemiddelde van de som van de kwadraten, dat wordt berekend door de som van de kwadraten te delen door de vrijheidsgraden.

• De kolom F-value is de teststatistiek van de F-test: het gemiddelde kwadraat van elke onafhankelijke variabele gedeeld door het gemiddelde kwadraat van de residuen. Hoe groter de F-waarde, hoe waarschijnlijker het is dat de variantie die met de onafhankelijke variabele samenhangt, echt is en niet door toeval kan worden verklaard.

• De kolom Pr(>F) is de p-waarde van de F-statistiek. Hieruit blijkt hoe waarschijnlijk het is dat de met de test berekende F-waarde zou zijn opgetreden als de nulhypothese van geen verschil tussen de groepsgemiddelden waar was.

Omdat de p-waarde van de onafhankelijke variabele, kunstmest, significant is (p < 0.05), is het waarschijnlijk dat het soort kunstmest een significant effect heeft op de gemiddelde gewasopbrengst.

Post-hoc-analyse voor ANOVA

Een ANOVA vertelt je of er verschillen bestaan tussen de groepen van de onafhankelijke variabele, maar niet welke verschillen significant zijn. Om na te gaan hoe de groepen van elkaar verschillen, voer je een TukeyHSD (Tukey’s Honestly-Significant Difference) post-hoc-analyse uit.

De Tukey-test vergelijkt de groepen twee aan twee en gebruikt een voorzichtige (conservatieve) foutschatting om de groepen te vinden die statistisch van elkaar verschillen.

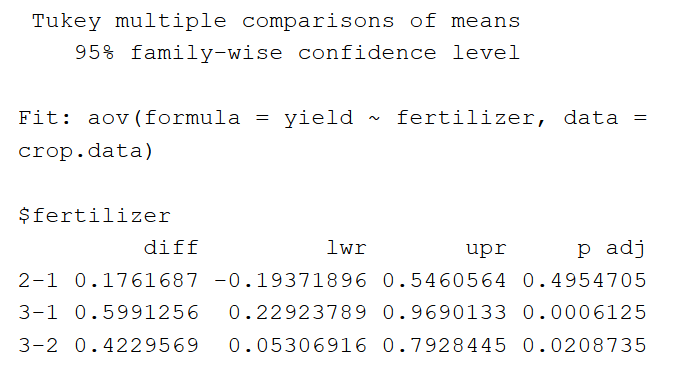
De output van de TukeyHSD ziet er als volgt uit:

Eerst vermeldt de tabel het geteste model (“Fit”). Vervolgens worden de parallelle verschillen tussen de groepen voor de onafhankelijke variabele vermeld.

Onder “$fertilizer” zien we het gemiddelde verschil tussen elke kunstmestbehandeling (“diff”), de onder- en bovengrens van het 95%-betrouwbaarheidsinterval (“lwr” en “upr”), en de p-waarde, gecorrigeerd voor meervoudige paarsgewijze vergelijkingen.

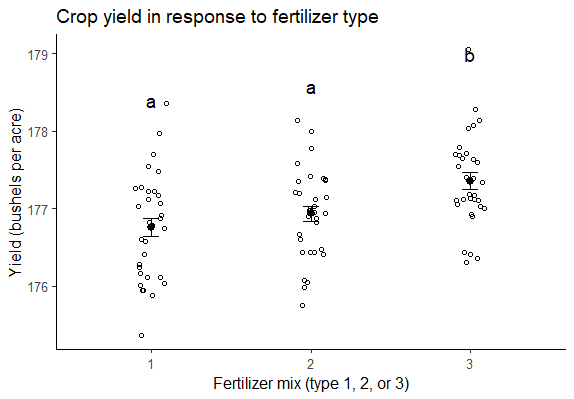
Uit de paarsgewijze vergelijkingen blijkt dat kunstmest 3 een significant hogere gemiddelde opbrengst heeft dan zowel kunstmest 2 als kunstmest 1, maar dat het verschil tussen de gemiddelde opbrengst van kunstmest 2 en 1 niet statistisch significant is.

Resultaten ANOVA rapporteren

Bij het rapporteren van de resultaten van een ANOVA geef je een korte beschrijving van de variabelen die je hebt onderzocht, de F-waarde, vrijheidsgraden en p-waarden voor elke onafhankelijke variabelen, en leg je uit wat de resultaten betekenen.

Als je meer gedetailleerde informatie wilt geven over de in je test gevonden verschillen, kun je ook een grafiek van je ANOVA-resultaten bijvoegen, met groepsletters boven elke groep van de onafhankelijke variabele om aan te geven welke groepen statistisch van elkaar verschillen:

Veelgestelde vragen over one-way ANOVA

Wat is het verschil tussen een one-way ANOVA en een two-way ANOVA?

Het enige verschil tussen een one-way ANOVA en een two-way ANOVA is het aantal onafhankelijke variabelen. Een one-way ANOVA heeft één onafhankelijke variabele, terwijl een two-way ANOVA er twee heeft.

• One-way ANOVA: Toetst de relatie tussen het merk schoen (Nike, Adidas, Saucony, Hoka) en de finishtijd van een marathon.

• Two-way ANOVA: Toetst de relatie tussen het merk schoen (Nike, Adidas, Saucony, Hoka), leeftijdsgroep van de loper (junior, senior, master) en de finishtijd van een marathon.

Alle ANOVA’s zijn bedoeld om te toetsen op verschillen tussen drie of meer groepen. Als je alleen op een verschil tussen twee groepen wilt testen, gebruik dan een t-toets.

Wat is een multivariate ANOVA (MANOVA)?

Je gebruikt een multivariate ANOVA (ook wel MANOVA) als je meerdere afhankelijke variabelen gebruikt. Je kunt deze ANOVA zowel gebruiken met één als meerdere groepsvariabelen (onafhankelijke variabelen).

Voorbeeld: Je wilt niet alleen niet alleen de gemiddelde lengte, maar ook het gemiddelde gewicht van verschillende groepen sporters vergelijken.

Je kunt beter een MANOVA uitvoeren dan meerdere losse ANOVA’s, om het risico op een Type I-fout te voorkomen.

Wat is een factoriële ANOVA?

Een factoriële ANOVA is elke ANOVA die meer dan één categorische onafhankelijke variabele gebruikt. Een two-way ANOVA is een soort factoriële ANOVA.

Enkele voorbeelden van scenario’s waarin je factoriële ANOVA’s gebruikt, zijn:

• Het toetsen van de gecombineerde effecten van vaccinatie (gevaccineerd of niet gevaccineerd) en gezondheidsstatus (gezond of al bestaande aandoening) op de mate van griepinfectie in een populatie.

• Het toetsen van de effecten van burgerlijke staat (gehuwd, ongehuwd, gescheiden, weduwnaar), beroepsstatus (zelfstandig, werkend, werkloos, gepensioneerd) en familiegeschiedenis (geen familiegeschiedenis, enige familiegeschiedenis) op de incidentie van depressie in een populatie.

• Het toetsen van effecten van het soort voeding (soort A, B of C) en stalbezetting (niet vol, enigszins vol, zeer vol) op het eindgewicht van kippen in een commercieel landbouwbedrijf.

Hoe wordt statistische significantie berekend in een ANOVA?

Bij een ANOVA is de nulhypothese dat er geen verschil is tussen de groepsgemiddelden. Als een groep significant verschilt van het algemene groepsgemiddelde, dan zal de ANOVA een statistisch significant resultaat rapporteren.

Significante verschillen tussen groepsgemiddelden worden berekend met behulp van een F-statistiek, die de verhouding weergeeft tussen de gemiddelde som van de kwadraten (de variantie die door de onafhankelijke variabele wordt verklaard) en de gemiddelde kwadratische fout (de variantie die overblijft).

Als de F-statistiek hoger is dan de kritieke waarde (de waarde van F die overeenkomt met je alfa-waarde, meestal 0.05), dan wordt het verschil tussen groepen statistisch significant geacht.

Wat is het verschil tussen een kwantitatieve en categorische variabele?

Er kan een onderscheid worden gemaakt tussen kwantitatieve en categorische variabelen:

• Bij kwantitatieve variabelen representeren de data hoeveelheden (zoals een lengte, gewicht, leeftijd).
• Bij categorische variabelen representeren de data groepen, zoals een ranking (bijvoorbeeld de eindposities bij het songfestival), classificaties (bijvoorbeeld kledingmerken), en binaire verdelingen (zoals kop of munt).