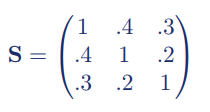Statistische resultaten rapporteren: Hoe doe je dat?
Voor het rapporteren van statistische onderzoeksresultaten in je scriptie bestaan richtlijnen, bijvoorbeeld voor de schrijfwijze van afkortingen, symbolen, vergelijkingen en formules. Dit artikel volgt de richtlijnen van de APA-stijl.
Significantie rapporteren
Als je de significantie van een statistische toets, zoals de t-toets of ANOVA rapporteert, moet je rekening houden met enkele regels. De significantie wordt weergegeven met de p-waarde (p = .076). Let bij het rapporteren op de volgende zaken:
- In het Nederlands wordt normaliter een komma gebruikt als decimaalteken, in het Engels een punt
- Bij statistische resultaten wordt ook in het Nederlands een punt gebruikt als decimaalteken
- Er staat geen nul voor de komma of punt
Voor waarden kleiner dan .001 gebruik je < .001 en rond je niet af naar .000. Met een p-waarde van .000 zou je immers aangeven dat iets onmogelijk is.
In tabellen wordt de significantie van een parameter vaak aangeduid met sterretjes (*). Dit geeft de lezer een snel overzicht van de parameters die significant zijn. Het aantal sterretjes geeft het significantieniveau aan. Voor p < .050 wordt één ster gebruikt, voor p < .010 twee sterren en voor p < .001 drie sterren.
Vergelijkingen rapporteren
Bij het schrijven van wiskundige vergelijkingen moet op een aantal punten gelet worden:
- Gebruik spaties, dus a + b = c in plaats van a+b=c
- Sluit vergelijkingen af met een punt
- Cursiveer de variabelen (in dit geval a, b en c)
- Gebruik haakjes om de volgorde van bewerkingen aan te geven, bijvoorbeeld: (a / b) + c in plaats van a / b + c
Vergelijkingen mogen in de tekst worden geplaatst, maar gecentreerd op een aparte regel heeft de voorkeur. Nummer deze vergelijkingen, zodat je ernaar kunt verwijzen. Dit nummer is altijd rechts uitgelijnd.
Voorbeeld
Haakjes gebruiken
Het gebruik van haakjes is noodzakelijk bij het rapporteren van toetsen met vrijheidsgraden, zoals de t-toets. Schrijf dus t(28) = -4.34 om aan te geven dat de betreffende t-toets 28 vrijheidsgraden had.
Verder kunnen haakjes gebruikt worden om na een uitspraak als ‘een klein percentage’ of ‘de toets is niet significant’ de precieze waarde te vermelden in de tekst.
Voorbeelden
- Slechts een klein percentage van de proefpersonen (2%) antwoordde ‘ja’.
- De variabele temperatuur is geen significante voorspeller (p = .342) voor het aantal drenkelingen.
Subscripts en superscripts
Bij het schrijven van vergelijkingen en formules in de statistiek wordt veel gebruikgemaakt van subscripts en superscripts. Voorbeelden hiervan zijn: xi2, x̄mannen en H0. Een aantal richtlijnen hierbij zijn:
- Schrijf xi2 en niet x2i. Subscripts komen namelijk voor superscripts als ze niet op boven elkaar gedrukt kunnen worden.
- Accenten staan boven de variabele, maar niet boven een sub- of superscript: dus x̄mannen en niet xmannen.
Lees waarom zo veel studenten Scribbr inschakelen
Afkortingen
Afkortingen in je scriptie horen op de juiste manier geïntroduceerd te worden. Bij het rapporteren van (statistische) resultaten schrijf je de termen zoals standaarddeviatie en correlatie helemaal uit en gebruik je dus niet een afkorting, zoals SD.
Bij het formuleren van hypotheses of in formules maak je wel gebruik van afkortingen.
Voorbeeld
De verwachting is dat de gemiddelde lengte van mannen hoger uitvalt dan de gemiddelde lengte van vrouwen. De nulhypothese is:
H0: μmannen ≤ μvrouwen
Percentages
In de lopende tekst gebruik je het procentteken (%) alleen wanneer er een getal aan voorafgaat. Wanneer dit niet het geval is, schrijf je ‘procent’ volledig uit. Om ruimte te besparen gebruik je in tabellen en figuren altijd het procentteken.
Voorbeeld
Uit onderzoek blijkt dat 5% van de mannen langer is dan 1,98m. Het overige percentage mannen was kleiner dan 1,98m of had geen lengte ingevuld.
Cursief, vet en romein
Bij het rapporteren van statistische analyses worden vaak Griekse of Latijnse letters en symbolen gebruikt. In sommige gevallen worden deze romein (normaal), cursief of dikgedrukt weergegeven.
Romein
De symbolen die je gebruikt voor uitspraken over de populatie worden normaal (romein) gedrukt. Voorbeelden hiervan zijn Griekse letters voor het gemiddelde (μ), de standaarddeviatie (σ) en de correlatie (⍴) die betrekking hebben op de populatie.
Uitspraken over de populatie doe je alleen in aannames en hypotheses. In je resultatenhoofdstuk schrijf je namelijk over de resultaten bij de onderzochte steekproef.
Cursief
Symbolen, letters en variabelen die gebruikt worden voor uitspraken over de steekproef moeten cursief worden gedrukt. Voorbeelden hiervan zijn:
- Latijnse letters voor de steekproefgrootte (N), het gemiddelde (M), de standaarddeviatie (s) en de correlatie: (r)
- Toetswaarden zoals F en t voor respectievelijk de ANOVA- en de t-toets
- De p-waarde, die de significantie aangeeft
- De naam van variabelen zoals lichaamslengte en gewicht
Vet
Dikgedrukte tekst gebruik je vrijwel nooit bij het rapporteren van resultaten. Dit is voorbehouden aan matrices en vectoren, zoals de S voor de covariantiematrix:
Getallen en decimalen
Voor het rapporteren van getallen en decimalen is het goed om te weten dat er een verschil bestaat tussen Nederlandse en Engelse richtlijnen. Scheidingstekens zoals puntkomma’s en punten zijn in het Engels vaak anders dan in het Nederlands.
Duizendtallen
Nederlands
In het Nederlands gebruik je punten om duizendtallen en komma’s om eenheden kleiner dan één te scheiden.
Voorbeelden
- De duurste koptelefoon kost € 1.600
- De gemiddelde prijs voor een kilo appels is € 1,52
Engels
In het Engels gebruik je komma’s voor het scheiden van duizendtallen en punten voor eenheden kleiner dan één.
Voorbeelden:
- The most expensive headphones cost €1,600
- The average price of a kilo of apples is €1.52
Puntkomma’s
Nederlands
In het Nederlands wordt een komma gebruikt voor eenheden kleiner dan één. Wanneer waardes gescheiden moeten worden, wordt een puntkomma gebruikt.
Voorbeeld
“Voor zijn tentamens haalde hij een 6,5; 9,7; 8,3; en 7,4.”
Engels
In het Engels worden komma’s gebruikt om waardes van elkaar te scheiden:
Voorbeeld
“His exam results were 6.5, 9.7, 8.3, and 7.4.”
De laatste (punt)komma in de opsomming is een zogeheten Oxford-komma en wordt gebruikt om duidelijk te maken dat het om twee verschillende tentamens gaat. De 8,3 en 7,4 zijn dus geen punten voor hetzelfde tentamen.
Getallen uitschrijven
De richtlijnen voor het uitschrijven van getallen verschillen voor het Nederlands en Engels. In het Nederlands schrijf je getallen onder de twintig en ronde getallen helemaal uit. Echter, hier zijn wat uitzonderingen op.
In het Engels schrijf je getallen van nul tot en met negen volledig uit, een aantal uitzonderingen daargelaten.
Statistieken, wiskundige formules en ratio’s worden nooit uitgeschreven.
Hoeveel decimalen moet je gebruiken?
Het aantal decimalen dat je gebruikt, hangt samen met het meetniveau dat je hebt toegepast. Hier zijn geen algemeen geldende regels voor. Wel kun je te veel of te weinig decimalen gebruiken.
Zo kan het bij een verkeerde keuze lijken dat je iets met grote precisie hebt gemeten, terwijl dat niet zo is of juist dat je data niet precies genoeg hebt weergegeven.
Te veel decimalen
De gemiddelde lengte van de respondenten is 178,385 centimeter.
Toelichting:
Door drie decimalen te gebruiken, lijkt het erop dat de gemiddelde lengte met grote precisie is gemeten, terwijl in werkelijkheid vaak alleen wordt gesproken over lengte in hele centimeters. In dit voorbeeld zou het gebruik van maximaal één decimaal volstaan.
Te weinig decimalen
Het gemiddelde uurloon van twintigjarigen is € 8.
Toelichting:
Door het gemiddelde te rapporteren zonder decimalen is het getal niet precies genoeg. Voor veel twintigjarigen verschilt een uurloon tussen € 8,01 en € 8,99 immers aanzienlijk. Daarnaast wordt het uurloon in veel gevallen weergegeven in twee decimalen.
Juiste aantal decimalen
Wanneer de lengte van respondenten is gemeten in centimeters (bijvoorbeeld 182 cm), dan is het gebruikelijk om één decimaal te gebruiken voor het gemiddelde of de standaarddeviatie hiervan. Dus: M = 176.2; SD = 13.5.
Veelgestelde vragen
Citeer dit Scribbr-artikel
Als je naar deze bron wilt verwijzen, kun je de bronvermelding kopiëren of op “Citeer dit Scribbr-artikel” klikken om de bronvermelding automatisch toe te voegen aan onze gratis Bronnengenerator.
van Heijst, L. (2023, 13 maart). Statistische resultaten rapporteren: Hoe doe je dat?. Scribbr. Geraadpleegd op 15 juli 2025, van https://www.scribbr.nl/statistiek/schrijfwijze-statistische-resultaten/